[자료구조] - 재귀(recursive) &유클리드 호제법 (C)

출처 | DO IT C언어 자료구조 입문편

그림 출처 | https://ahribori.com/article/59262cf0c686bd0d48e960e2

재귀란

어떤 사건이 자기 자신을 포함하고 자기 자신을 사용하여 정의될 때 재귀적이라고 한다.

이와 같은 정의를 따른다. 
1. 1은 자연수다.
2. 자연수 n의 바로 다음 수도 자연수다.

순차곱셈 구하기 예제

기본적인 원리(조건)
1. 0! = 1
2. n > 0이면 n! = n * (n-1)!
ex) 10! = 10  * 9! / 9! = 9 * 8!

<코드 구현>

#include <stdio.h>


int factorial(int n)
{
	if (n > 0)
		return n * factorial(n - 1);
	else
		return 1;
}

int main()
{
	int x;
	printf("정수를 입력하세요 : ");
	scanf_s("%d", &x);
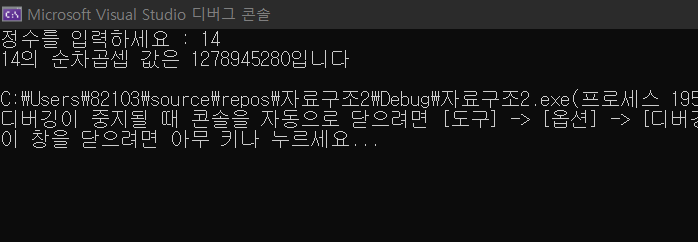
	printf("%d의 순차곱셉 값은 %d입니다 \n", x, factorial(x));
	return 0;

}

• 재귀함수
  • factorial함수를 이용해 3의 순차곱셈 값을 구체적으로 구하는 과정을 표현해라.
  • 3 x factorial(2) => 3 x 2 .....4(순서)
  • 2 x factorial(1) => 2 x 1 ..... 3
  • 1 x factorial(0) => 1 x 1 ..... 2
  • 0 x factorai(음수) => 1반환 ..... 1

<결과>

직접 재귀와 간접 재귀

직접 재귀 : 자신과 같은 함수를 호출하면 직접 재귀다.

간접 재귀 : 함수 a가 함수 b를 호출하고 다시 함수 b가 함수 a를 호출하는 구조로 이루어진다.

<그림 출처 | https://hayeon17kim.github.io/posts/doit05/>

유클리드 호제법

<증명>

유클리드 호제법이란 큰 값에 대한 GCD(최대공약수)를 구하는 알고리즘을 말한다.

2개의 자연수 A,B가 있고 A%B=r이라고 했을 때 다음을 만족한다.

위 식을 증명하기 위해선 최대공약수의 개념을 이용해야 한다. A,B에게 G라는 최대공약수가 있다면 다음과 같이 나타낼 수 있다.

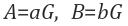
G가 최대공약수이기 때문에 a,b는 반드시 서로소(공약수가 1뿐인 수)여야 한다.

A를 B로 나눈 나머지가 r이기 때문에 그 몫을 q라고 한다면 다음의 식들이 유도된다.

r과 B가 G라는 공약수를 갖는데 이 공약수가 최대공약수임을 증명하면 되니까 a-bq와 b가 서로소임을 증명하면 된다.

여기서 서로소가 아니라고 하면 두 수는 공약수를 갖기 때문에 다음과 같이 나타낼 수 있다.

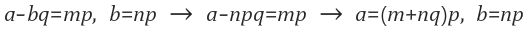
여기서 a,b는 서로소인데 p라는 공약수를 갖으므로 조건에 위배된다. 따라서, a-bq와 b는 서로소이다.

결국, B와 r의 최대공약수는 G이다. 이렇게 유클리드 호제법이 증명된다.

ex : gcd(12345, 123) = gcd(123, 45)
     gcd(45, 33) => gcd(33, 12) => gcd(12, 9) => gcd(9,3) => gcd(3,0) 
     
     ▶ 3 

다음은 코드로 표현해보겠다.

#include <stdio.h>

int gcd(int x, int y)
{
	if (y == 0)
		return x;
	else
		return gcd(y, x % y);

}


int main()
{
	int x, y;
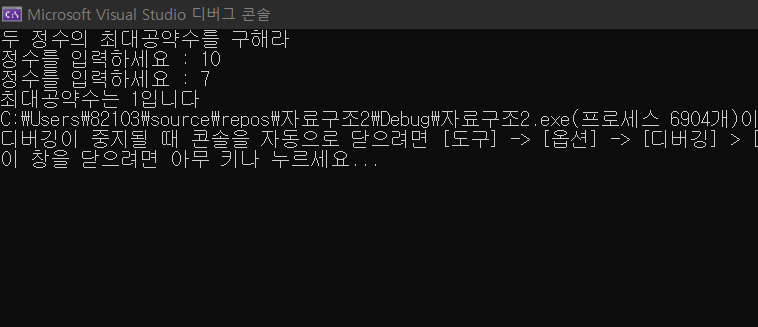
	puts("두 정수의 최대공약수를 구해라");
	printf("정수를 입력하세요 : ");
	scanf_s("%d", &x);
	printf("정수를 입력하세요 : ");
	scanf_s("%d", &y);
	printf("최대공약수는 %d입니다.\b", gcd(x, y));

}

<결과>