이번 시간엔 최대부분배열을 구현해보자.
1. 문제
- 길이가 n인 배열 A[0], A[1], ..., A[n-1] 이 입력으로 주어 질때, i번째부터 j번째까지 원소드로 이루어진 배열 A[i], ..., A[j] 를 부분배열이라고 하고, A[i, j] 로 나타낸다.
- 부분 배열의 속한 원소들의 합이 최대가 되는 부분 배열을 구하는 것이 이 문제의 목적이다.
이 때 길이가 0인 부분배열도 허용하며, 이 부분배열의 원소들의 합은 0이라고 정의한다.
예를 들어, 아래와 같은 배열이 있다면,
-2 -1 3 5 2 -5 0 2면 이 배열의 최대부분배열의 합은 10이다(3+5+2)
2. 해결방법
-
최대부분배열의 원소합을 구하는 알고리즘에는 크게 4개가 있다.
-
완전탐색, 중복제거한 탐색, 분할정복법, 동적계획법
1) 완전탐색(브루트포스 알고리즘) - 시간복잡도 O(n^3)
-
단순히 모든 부분배열을 비교하여 최대인 배열을 구하는 알고리즘이다.
-
MaxSum은 최종 결과합, ThisSum은 각 부분배열의 합을 저장하는 변수
-
삼중반복문을 이용하여 i(0,n)~j(i,n)까지의 부분배열을 구한다.
int MaxSubarray1(int A[], int N)
{
int MaxSum, ThisSum;
int i, j, k;
MaxSum = 0;
for (i = 0; i < n; i++) {
for (j = i; j < n; j++) {
ThisSum = 0;
for (k = i; k <= j; k++)
ThisSum = ThisSum + A[k];
MaxSum = max(MaxSum, ThisSum);
}
}
return MaxSum;
}- 시간복잡도 구하기
시간복잡도는 명령실행개수를 구하는 것!
데이터의 개수가 n개일 때 for문 하나당 O(n) 시간이 걸린다고 생각하면 편함(for문 안이 상수시간이 걸릴 때)
따라서 3중 반복문이므로 O(n x n x n) = O(n^3) 이다.
- 특징 : 시간복잡도가 O(n^3) 이기 때문에 데이터의 개수가 많아질수록 시간이 기하급수적으로 오래 걸림
2) 중복을 제거한 탐색
-
1번 방법에서 중복을 제거한 방법이다
-
1번 방법에서는 모든 부분배열의 원소의 합을 각각 다 구하기 때문에 중복계산이 많다
예를 들어 [0,2]의 부분배열의 합([0]+[1]+[2])을 구해도 다음번 [0,3]의 부분배열은 [0]+[1]+[2] 의 연산을 다시해야 한다.
이 것을 보완한 알고리즘이 2번 알고리즘이다.
int MaxSubarray2(int A[], int N)
{
int MaxSum, ThisSum;
int i, j;
MaxSum = 0;
for (i = 0; i < n; i++) {
ThisSum = 0;
for (j = i; j < n; j++) {
ThisSum = ThisSum + A[j];
MaxSum = max(MaxSum, ThisSum);
}
}
return MaxSum;
}- 시간복잡도 구하기
이중반복문이므로 O(n^2) 이 걸린다. (1번참고)
이 알고리즘 또한 데이터의 개수가 많아질수록 시간이 기하급수적으로 오래걸린다.
3) 분할정복법
-
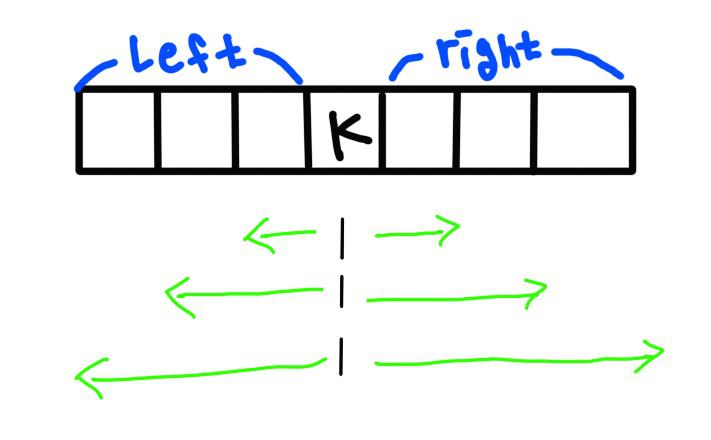
부분배열의 중간값의 인덱스를 k(임의의 수)라고 했을때
-
k보다 왼쪽에 있으면 left, 오른쪽에있으면 right라고 하자.
-
그러면 모든 부분배열은 left에 있는 부분배열, right에 있는 부분배열, left와 right에 걸쳐있는 부분배열 중 하나일 것
ex: 0 1 2 3 k=4 5 6 7 8
-
예를 들면 0~3에 있는 부분배열 ,5~8에 있는 부분배열, 4를 포함하여 걸쳐있는 부분배열 이 있을 것이다.
-
그러면 순환호출(재귀)를 이용하여 각각에 속해있는 부분배열의 합을 구할 수 있다.
(left에 있는 부분배열을 중간값을 정해 left안의 left, right를 구하고.. .또 구하고. 이런식으로)걸쳐있는 부분배열은? -> 왼쪽과 오른쪽의 부분배열을 합치면 된다!
- 그러면 최대부분배열은? (key)
왼쪽에서의 부분배열의 최대값과 오른쪽에서의 부분배열의 최대값과 왼쪽과 오른쪽에 걸친 부분배열을 비교하여
가장 큰 값이 전체배열의 최대부분배열의 원소의 합이 될 것이다.
다음 이미지를 보자,
int MaxSubarray3(int A[], int Left, int Right)
{
int MaxSum, MaxLeft, MaxRight, MaxCenter;
int MaxCenterL, MaxCenterR, ThisSum;
int Center, i;
if (Left == Right) {
if (A[Left] > 0) return A[Left];
else return 0;
}
Center = (Left + Right) / 2;
MaxLeft = MaxSubarray3(A, Left, Center);
MaxRight = MaxSubarray3(A, Center + 1, Right);
MaxCenterL = 0;
ThisSum = 0;
for (i = Center; i >= Left; i--) {
ThisSum = ThisSum + A[i];
MaxCenterL = max(MaxCenterL, ThisSum);
}
MaxCenterR = 0;
ThisSum = 0;
for (i = Center + 1; i <= Right; i++) {
ThisSum = ThisSum + A[i];
MaxCenterR = max(MaxCenterR, ThisSum);
}
MaxCenter = MaxCenterL + MaxCenterR;
MaxSum = max(max(MaxLeft, MaxRight), MaxCenter);
return MaxSum;
}먼저 함수의 인수를 보자.
A[] 은 입력된 배열, left는 가장 왼쪽에 있는 인덱스 0, right는 가장 끝쪽에 있는 인덱스 n-1이 될 것이다.
(왜냐하면 배열의 크기가 n이므로 가장 끝에 있는 배열의 인덱스는 n-1)
선언된 변수를 보자.
MaxSum = 최종 부분배열원소의 최대값
MaxLeft = 왼쪽에 있는 부분배열의 최대값
MaxRight = 오른쪽에 있는 부분배열의 최대값
MaxCenter = 양쪽에 걸쳐있는 부분배열의 최대값
MaxCenterL = 왼쪽배열의 부분배열의 최대값
MaxCenterR = 오른쪽배열의 부분배열의 최대값
(조건문)
if (Left == Right) {
if (A[Left] > 0) return A[Left];
else return 0;
}
왼쪽과 오른쪽의 인덱스가 같을 때이다. 즉 배열의 크기가 1일 때 재귀함수가 끝난다.(중앙값(k) Left와 Right의 평균값)
Center = (Left + Right) / 2;
MaxLeft = MaxSubarray3(A, Left, Center);
MaxRight = MaxSubarray3(A, Center + 1, Right);
MaxCenterL = 0;
순환 호출을 이용하여 구하려는 배열의 크기가 0이 될 때까지 부분배열을 구한다.
(반복문)
for (i = Center; i >= Left; i--) {
ThisSum = ThisSum + A[i];
MaxCenterL = max(MaxCenterL, ThisSum);
}
i가 center부터 left까지 감소하면서 부분배열의 합을 구한다.
그리고 합을 구하면서 부분배열의 최대값을 구한다.MaxCenter = MaxCenterL + MaxCenterR;
MaxSum = max(max(MaxLeft, MaxRight), MaxCenter);
걸쳐있는 배열은 left배열에서의 최대값과 right배열에서의 최대값을 더한 값
최종 결과값은 left, right, center에서 가장 큰 값이 최대부분배열의 원소의 합이 된다. 시간복잡도 구하기
T(n) 을 길이가 n인 배열에서 최대 부분 배열을 구하는 데 걸리는 시간이라고 하자.
n=1 일때(배열의 크기가 1일때) 에는 left랑 right가 (0일때)같을 때 즉 if문을 수행하므로 상수시간(O(1)) 이다.
n>=2 인 경우에는 배열을 반으로 나누어 n/2인 배열 각각에 대해 순환호출을 한다.
두개의 for문을 수행하는데 각각 O(n)시간 걸리므로
총 걸리는 시간 T(n) =2*T(n/2)(순환호출을 부르는 시간) + O(n) 이다.
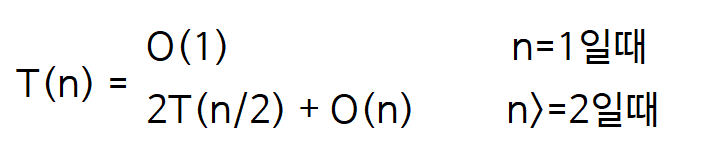
그러면 수학적 계산(점화식)으로 시간복잡도를 구해보자

시간 복잡도는 O(nlogn) 이다.
4. 동적계획법(dp)
-
부분 배열의 오른쪽 끝이 A[k] 인 최대 부분 배열의 원소의 합을 S[k] 라고 하자
-
그러면 최대부분배열 원소합은 S[0], S[1], ... , S[n-1] 중 하나일 것이다.
S[k] = max{S[k-1] + A[k], 0}
위 식을 증명해보자
오른쪽 끝이 A[k]인 최대 부분배열의 길이는 0이거나 1이상일 것이다.
길이가 0인 경우, S[k] = 0
길이가 1이상인 경우,
S[k]에서 원소 A[k](오른쪽 끝에있는 원소)를 제거하면 오른쪽 끝이 A[k-1]인 최대 부분배열이 된다.
<코드>
int MaxSubarray4(int A[], int N)
{
int MaxSum, ThisSum;
int k;
MaxSum = 0;
ThisSum = 0;
for (k = 0; k < n; k++) {
ThisSum = max(ThisSum + A[k], 0);
MaxSum = max(MaxSum, ThisSum);
}
return MaxSum;
}- 시간복잡도 구하기
어렵지 않게 시간복잡도는 O(n)이라는 사실을 알 수있다.