이번 시간에는 트리에 대해서 알아보겠다.
트리
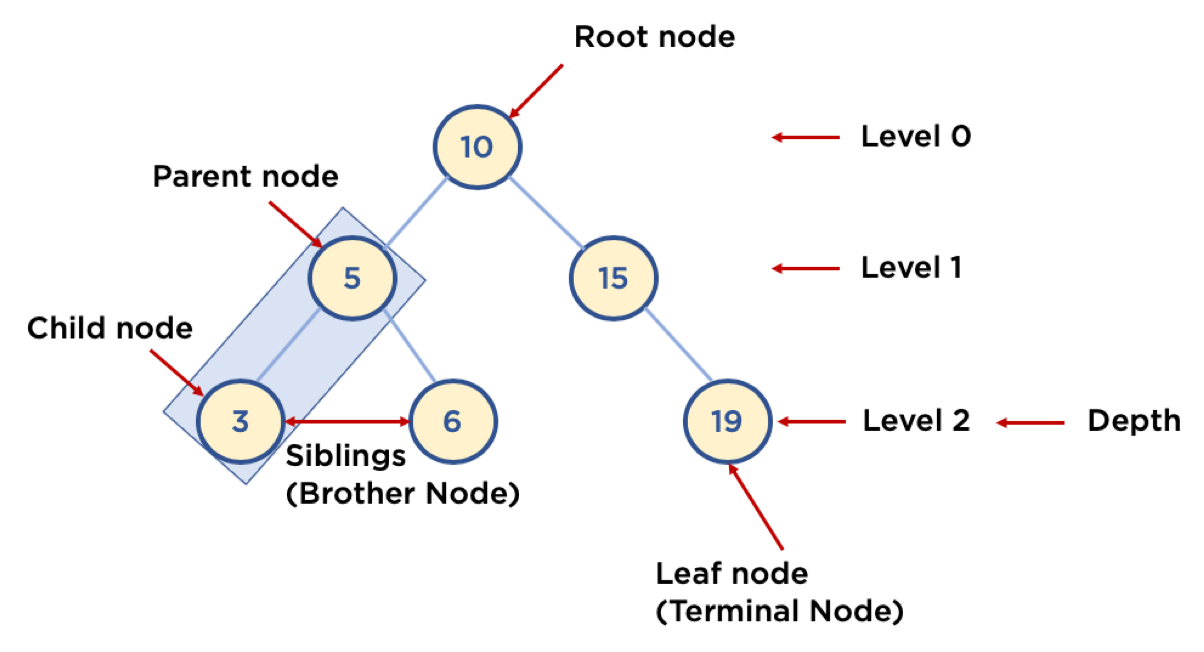
<용어 정리>
노드 : 트리의 구성요소
루트 : 부모가 없는 노드
레벨 : 트리의 각층 번호
높이 : 트리의 최대레벨
차수 : 노드가 가지고있는 자식노드의 개수
간선 : 트리에 연결된 모든선
서브트리 : 하나의 노드와 자손들로 이루어진 트리
형제노드 : 같은 레벨의 노드
후손노드 : 임의의 노드 하위에 연결된 모든 노드
단말노드 : 자식이 없는 노드
비단말노드 : 하나이상의 자식을 가지는 노드
위에서 루트노드는 10이다.
트리의 재귀적 정의를 살펴보자.
1, 트리는 하나 이상의 노드로 구성된 유한 집합으로써 특별히 지정된 노드인 (root)가 있고
2. 루트를 제외한 나머지 노드들은 각각이 트리이면서 서로 교차하지 않는 분리된 집합 T1, T2, ,,,, Td로 분할된다. 이 때 각각의 Ti를 루트의 부분트리라고 한다.
여기서 말하는 트리는 루트가 있는 트리(rooted tree)이고, 루트를 정의하지 않는 트리를 자유 트리(free tree)라고 부르는데, 이 때 트리는 연결되어 있고 사이클이 없는 그래프를 말한다.
각 노드의 data 필드와 분지수 만큼의 link 필드를 가지고
노드의 link는 왼쪽부터 차례로 자식 노드를 가리킨다.
d>>2이면 null 링크 수가 dn-(n-1)로 메모리 낭비가 심하다.
이진트리란?
1. 모든 트리를 이진 트리(binary tree)로 표현할 수 있다. 이진 트리란 분지수가 2 이하인 트리를 말한다
2.각 노드의 link는 부모-자식의 관계를 표현하는 것이 아니라, 하나는 첫 번째 자식 노드를 가리키고 다른 하나는 바로 다음 형제 노드를 가리킨다.
3. 트리에선 왼쪽 자식노드와 오른쪽 자식노드가 다르다.
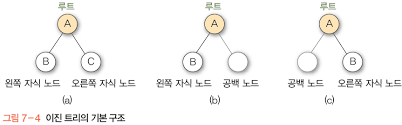
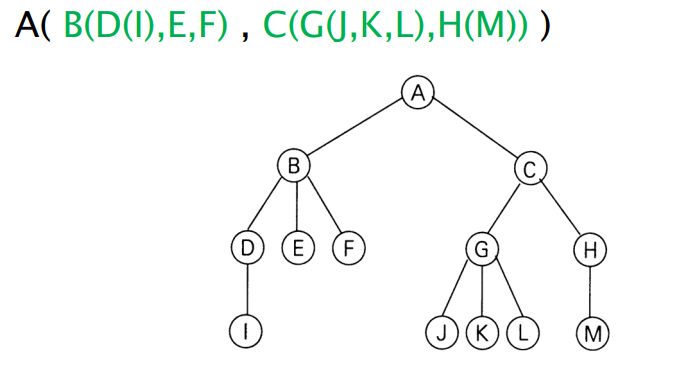
괄호를 이용한 트리의 표현
트리는 괄호를 이용하여 리스트 표현을 할 수 있다. 이 때 각 부트리는 역시 리스트 표현을 한다
이진트리의 재귀적 정의
- 이진 트리는 노드의 유한 집합으로써, 노드의 집합이 공집합이거나, 루트와 함께 왼쪽 부분트리, 오른쪽 부분트리라고 부르는 두 개의 서로 다른 이진 트리로 구성된다.
- 이진 트리는 분지수가 2 이하인 트리이다.
- 이진 트리에서는 왼쪽 부분트리와 오른쪽 부분트리를 구분하여 말한다
이진 트리의 특별한 경우로 다음과 같은 것이 있다.
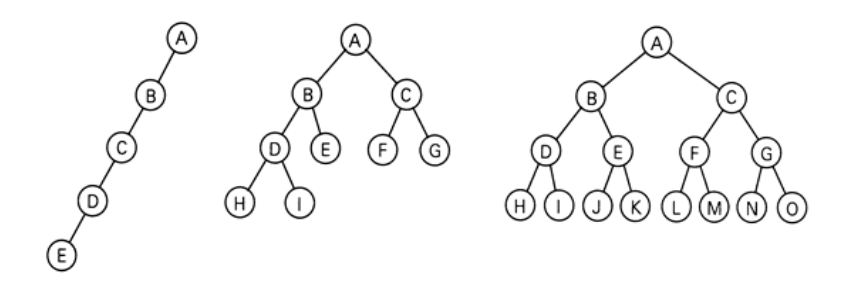
◦ 경사 이진 트리(skewed binary tree; 사향 이진 트리)
◦ 완전 이진 트리(complete binary tree)
: 완전이진트리는 트리를 구성하고 있는 임의의 두 단말 노드의 레벨 차수가 1이하이다. 마지막 레벨을 제외한 모든 레벨은 존재할 수 있는 모든 노드를 가지며 왼쪽에서 오른쪽으로 채워지는 이진트리다.
◦ 포화 이진 트리(full binary tree)
이진 트리의 성질
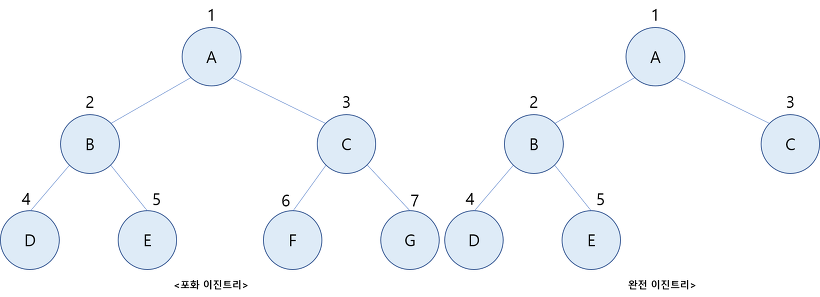
위 포화 이진트리 같은 경우에는 루트 노드를 1번으로 하고 레벨별로 왼편에서 오른 편오로 차례로 노드 위치에 번호를 까지 부여가 가능하다. 그런데 만일 높이가 h이고 노드 수가 n, 일때 n<=()인 이진트리를 노드의 레벨 순수에 따라 노드 번호를 붙인다면 이때 각 노드 번호의 위치가 포화 이진트리 번호 1에서 n까지의 위치와 모두 정확하게 일치한다면 이 트리를 완전 이진트리라고 한다. 즉 루트 노드를 1이라고 하고 그외에 모든 노드가 왼쪽에서부터 오른쪽까지 꽉 차서 노드의 수가 n<=()라면 완전 이진트리이다. 아래 그림은 완전 이진트리의 예이다.
1.레벨 𝑖에 있는 노드의 최대 개수는 2^𝑖이다.
2.깊이가 𝑘인 이진 트리의 최대 노드 개수는 밑 사진과 같다.
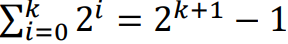
이진트리의 순차표현
이진 트리는 유일하게 붙여지는 포화 이진 트리 번호를 이용하면 순차 표현 즉 1차원 배열로 쉽게 표현할 수 있다. 즉 포화 이진트리 번호를 배열의 인덱스로 사용하면 된다. 아래 그림은 이진 트리의 순차표현을 보여준다. 이때 1차원 배열에시 인덱스 0은 실제 사용하지 않고 인덱스 1은 항상 루트 노드를 나타낸다.
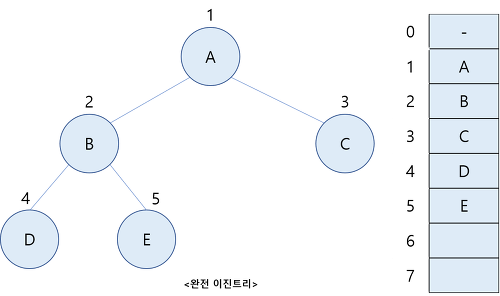
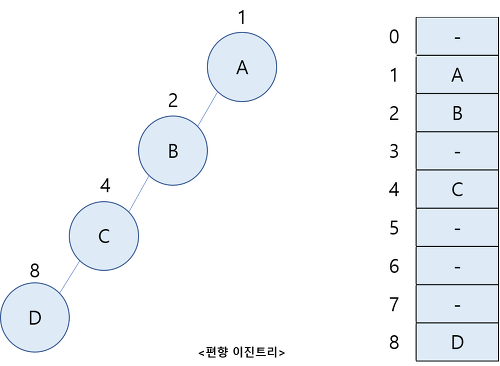
n개의 노드를 가진 이진트리를 1차원 배열로 표현했을 때 포화 이진트리 번호를 인덱스로 사용하면 어떤 노드 i의 부모, 왼쪽자식, 오른쪽 자식의 인덱스를 쉽게 알 수 있다. 아래 표는 완전 이진트리를 표현한 1차원 배열에서 인덱스 관계이다.
목표 노드 인덱스 값 조건
노드 i의 부모 [ i / 2 ] i > 1
노드 i의 왼쪽자식 2 * i 2 * i <= n
노드 i의 오른쪽 자식 2 * i +1 (2 * i + 1) <= n
루트 노드 1 0 < n
이진트리의 치명적인 단점이 있다. 모든 이진트리를 배열을 이용하여 표현할 수 있으나 대부분의 경우에는 많은 메모리를 낭비한다.
이진트리의 연결표현
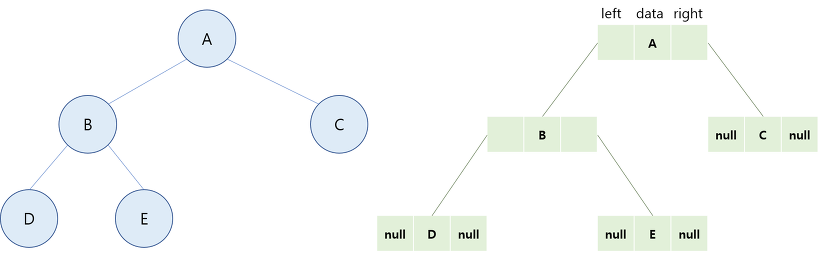
위와 같은 순차 표현의 문제 때문에 대부분의 경우에는 순차 표현보다는 연결 표현을 사용하고 있다. 이 연결표현을 위해서는 각 노드들을 다음 그림과 같이 left, data, right를 포함하는 구조를 가지고 있다. 여기서 필드 left, right는 각각 왼쪽 서브트리와 오른쪽 서브트리를 가리키는 링크이다. 이 노드 구조는 부모 노드를 찾기가 어렵다는 문제점이 있지만 꼭 필요한 경우에는 parent 필드를 추가해서 사용하면 된다

아래 그림은 완전이진 트리를 연결 표현으로 나타낸 것이다. 여기서 left와 right는 왼쪽 서브트리와, 오른쪽 서브트리를 가리키는 포인터 필드가 되며 만일 서브트리가 공백이면 해당 노드는 null이된다.
출처: https://kingpodo.tistory.com/27 [킹포도의 코딩]
출처: 자료구조[박정흠]