이진트리순회

이진 트리에서 가장 흔한 연산은 트리 순회, 즉 트리의 모든 노드
를 한번씩 방문하는 것이다.

한 노드에서 취할 수 있는방법은 모두 6개이지만 항상 왼쪽 서브트리를 순회 한다는것을 대전제로 3가지의 순회방법만 가능하게 된다. 그것이 중위 순회(inorder traversal), 후위 순회(postorder traversal), 전위 순회(preorder traversal)이다.

이것의 뜻을 간단히 알아보자면 루트노드의 순회가 왼쪽 서브트리와 오른쪽 서브트리에 중간에 행해지면 중위 순회, 루트노드의 순회가 가장 마지막에 행해지면 후위순회, 루트노드의 순회가 가장먼저 행해지면 전위 순회가 된다.

특히 산술식을 표현하는 이진트리를 중위, 후위, 전위 순회 방법으로 기술한 결과가 각각 중위 표기식, 후위 표기식, 그리고 전위 표기식이 된다.

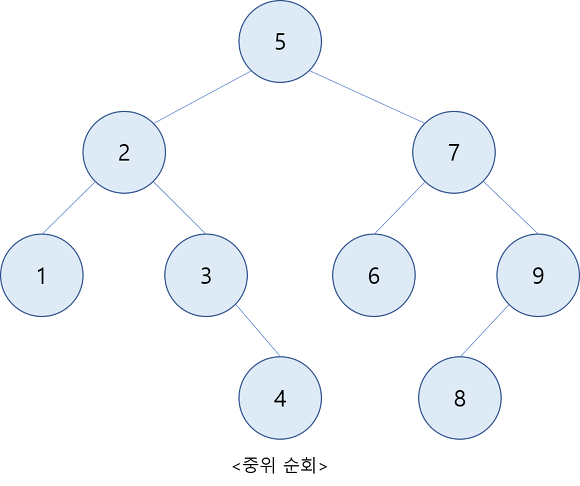
◦ 중순위 순회(inorder traversal)

1. 왼편 서브트리(left subtree)를 중위 순회한다.
2. 루트 노드(root node)를 방문한다.
3. 오른편 서브트리(right subtree)를 중위 순회한다.

중순위순회 비재귀적코드구현

//중순위순회 비재귀적표현

void inorder2(tree_pointer ptr)
{
	int top = 0;
	tree_pointer stack[N];
	
	while (1)
	{
		for (; ptr; ptr = ptr->left_child)
			push(&top, ptr);

		ptr = pop(&top);
		if (!ptr) break;
		printf("%d", ptr->data);
		ptr = ptr->right_child;
	}


}

중순위순회 코드구현

void inorder(tree_pointer ptr)
{
	if(ptr)
    {
    inorder(ptr->left_child);
    printf("%d", ptr->data);
    inorder(ptr->right_child);
    }

}

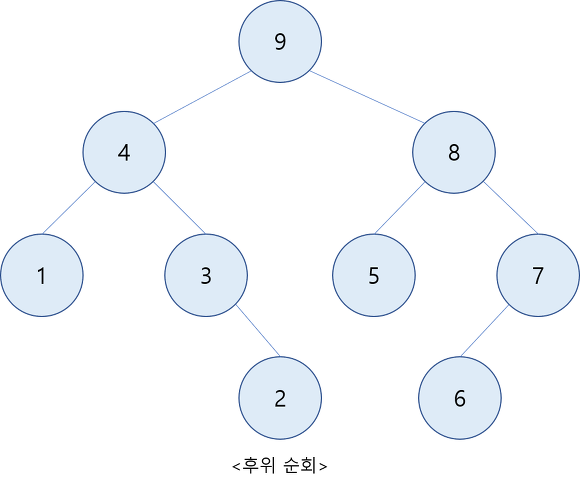
◦ 후순위 순회(postorder traversal)

1. 왼편 서브트리(left subtree)를 후위 순회한다.
2. 오른편 서브트리(right subtree)를 후위 순회한다.
3. 루트 노드(root node)를 방문한다.

후순위 순회 코드구현

void postorder(tree_pointer ptr)
{
	if(ptr){
    	postorder(ptr->left_child);
        postorder(ptr->right_child);
        printf("%d", ptr->data);
    }
}

◦ 전순위 순회(preorder traversal)

1. 루트 노드(root node)를 방문한다.
2. 왼편 서브트리(left subtree)를 전위 순회한다.
3. 오른편 서브트리(right subtree)를 전위 순회한다.

전순위 순회 코드구현

void preorder(tree_pointer ptr)
{
	if(ptr)
    {
    	printf("%d", ptr->data);
        preorder(ptr->left_child);
        preorder(ptr->right_child);
    
    }


}

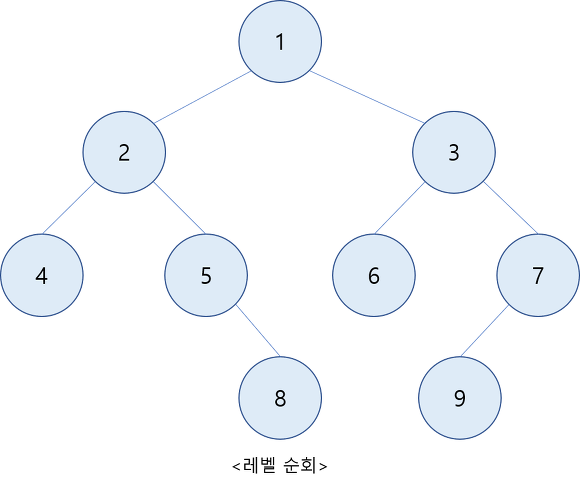
◦ 레벨순위 순회(level order traversal)

이진 트리는 노드의 레벨 순서로 순회할 수도 있다. 이를 위해서는 큐를 사용해야 한다. 순회는 처음에 루트 노드를 큐에 삽입하는것으로 시작한다.

그런 다음에 큐에 있는 노드들을 삭제하여 그 노드를 방문하고 그의 왼쪽 서브트리와 오른쪽 서브트리가 널이 아년 경우에 순서대로 큐에 삽입한다.

이 처리 과정을 큐가 공백이 될 때까지 반보가면 이진 트리를 레벨 순서로 방문한 결과가 된다.

레벨순위 순회

void levelorder(tree_pointer ptr)
{
	int front = rear = 0; // 큐 초기화
	tree_pointer queue[N];
	if (!ptr) return;
	enqueue(&rear, front, ptr);
	while (1) {
		ptr = dequeue(&front, rear);
		if (ptr) {
			printf("%d", ptr->data);
			if (ptr->left_child)
				enqueue(&rear, front, ptr->left_child);
			if (ptr->right_child)
				enqueue(&rear, front, ptr->right_child);
		}
		else break;
	}
}

참고 | 출처 : https://kingpodo.tistory.com/28?category=805745