Level Order Traversal

from collections import deque

def levelOrder(root):
	visited = []
    if root is None:
    	return 0
    q = deque()
    q.append(root)
    while q:
    	cur_node = q.popleft()
        visited.append(cur_node.value)
        
        if cur_node.left:
        	q.append(cur_node.left)
        if cur_node.right:
        	q.append(cur_node.right)
    return visited

응용1 - 각 레벨별 출력 with linked list

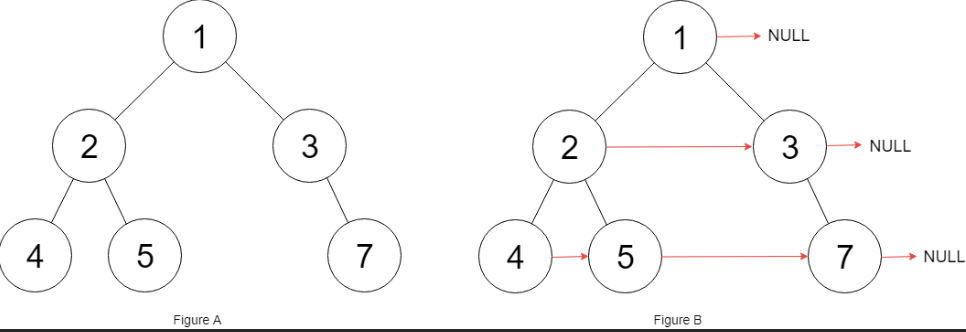
문제 : leetcode 117. Populating Next Right Pointers in Each Node II

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return None
        q = deque()
        q.append(root)
        dummy=Node(-999) # to initialize with a not null prev
        while q:
            length=len(q) # find level length
            
            prev=dummy
            for _ in range(length): # iterate through all nodes in the same level
                popped=q.popleft()
                if popped.left:
                    q.append(popped.left)
                    prev.next=popped.left
                    prev=prev.next
                if popped.right:
                    q.append(popped.right)
                    prev.next=popped.right
                    prev=prev.next                
                 
        return root

응용2 - 각 레벨당 평균 구하기 with binary tree node #BFS

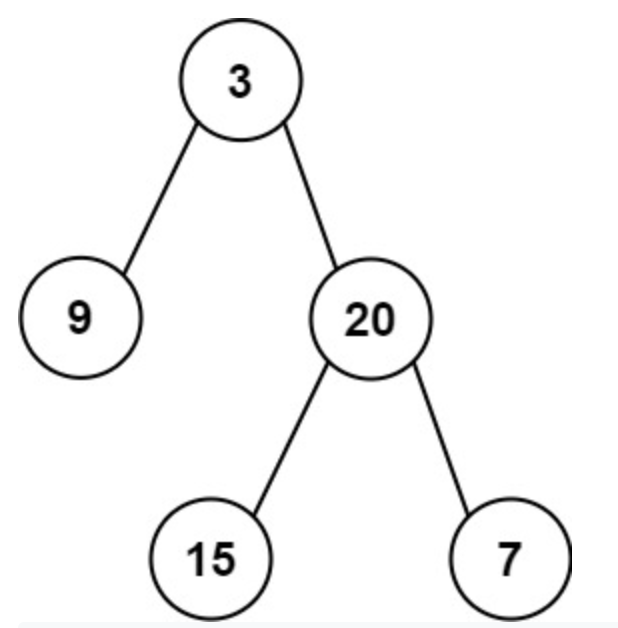
문제 : leetcode 637. Average of Levels in Binary Tree

from collections import deque
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        if root is None:
            return
        
        q = deque([])
        avg = []

        q.append(root)
        nodes_count_per_level = 0
        sum_per_level = 0

        q.append(None)

        while len(q) > 0:
            node = q.popleft()
            if node is None:
                avg.append(sum_per_level / nodes_count_per_level)
                sum_per_level = 0
                nodes_count_per_level = 0
                q.append(None)
                
                if q[0] is None:
                    break
                else:
                    continue
            
            sum_per_level += node.val
            nodes_count_per_level += 1

            if node.left is not None:
                q.append(node.left)

            if node.right is not None:
                q.append(node.right)
        return avg

queue 에 노드가 들어오고부터 None 이 나오기까지가 하나의 level 이다. 총합과 통계를 구해야 하니 총합과 노드의 수를 카운트한뒤 None 이 나올때 평균을 구하고 초기화해준다.이때 큐에 더 쌓인게 없다면 반복을 종료한다.

응용3 - 각 레벨의 노드 구하기 with binary tree node #BFS

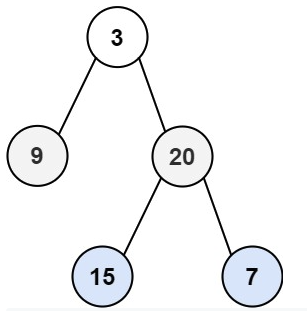
문제 : leetcode 102. Binary Tree Level Order Traversal

from collections import deque
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        nodes = []
        queue = deque([root])
        
        if root is None:
            return nodes
        
        while len(queue) > 0:
        	temp = []
            queueLen = len(queue)
            
            for _ in range(queueLen):
                node = queue.popleft()
                
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
                
                temp.append(node.val)
            nodes.append(temp)
            
        return nodes

응용 2 가 queue 에 레벨이 끝날 때마다 None 을 삽입해서 각 level 이 끝나는 것을 인지하는 방식이었다면 위의 풀이는 None 을 굳이 넣을 필요 없이 각 레벨에서의 노드의 수는 이전 레벨에서 큐에 쌓아둔 노드의 수만큼이니 그 길이만큼만 popleft 하는 방식으로 각 레벨의 노드만 조회할 수 있다. 이 방식이 좀 더 효율적인 것 같다.

응용 4 - 각 레벨별 지그재그로 출력 with binary tree node #BFS

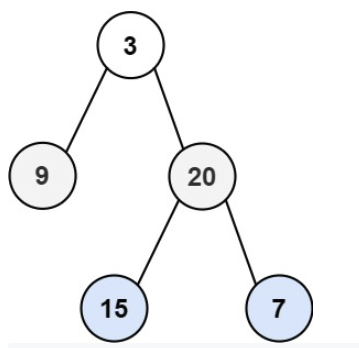
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]

from collections import deque
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if root is None:
            return root
        
        nodes = []
        queue = deque([root])
        
        flag = False
        
        while queue:
            temp = deque([])
            
            lenQ = len(queue)
            for _ in range(lenQ):
                node = queue.popleft()
                
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
                
                if flag:
                    temp.appendleft(node.val)
                else:
                    temp.append(node.val)
            flag = not flag
            nodes.append(list(temp))
        
        return nodes

앞의 풀이에서 몰랐던 사실이 deque 이라도 리스트에 아무것도 없어도 len 길이로 비교해야 한다고 생각했는데 아무것도 없을때 JS 의 Falsy 처럼 while queue: 로만 서도 while len(queue) > 0 과 같이 동작한다는 사실을 알게 되었다.

traversal

def traveral(root):
	if root is None:
    	return
    traversal(root.left)
    traversal(root.right)

preorder traversal

def preorder(root):
	if root is None:
    	return
    print(root)
    preorder(root.left)
    preorder(root.right)

inorder traversal

def inorder(root):
	if root is None:
    	return
   	inorder(root.left)
    print(root)
    inorder(root.right)

posorder traversal

def postorder(root):
	if root is None:
    	return
    postorder(root.left)
    postorder(root.right)
    print(root)

flatten tree

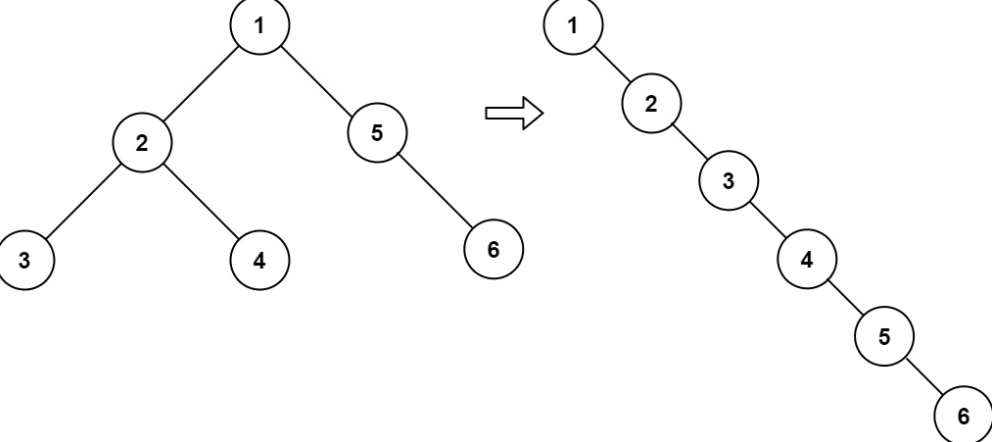
문제 출처 : leetcode 114. Flatten Binary Tree to Linked List

class Solution:
    def flatten(self, root: TreeNode) -> None:
        cur = root
        while cur:
            if cur.left:
                prev = cur.left
                while prev.right:
					prev = prev.right    # We go to left Subtree's rightMost Node
                
                prev.right = cur.right   #We make current Node's right Subtree prev's right Subtree
                cur.right = cur.left    # We make it right Subtree
                cur.left = None   # Removing left 
            
            cur = cur.right

참고 레퍼런스

개발자노씨