링크

문제 풀이

문제 설명

회사원 Demi는 가끔은 야근을 하는데요, 야근을 하면 야근 피로도가 쌓입니다. 야근 피로도는 야근을 시작한 시점에서 남은 일의 작업량을 제곱하여 더한 값입니다. Demi는 N시간 동안 야근 피로도를 최소화하도록 일할 겁니다.Demi가 1시간 동안 작업량 1만큼을 처리할 수 있다고 할 때, 퇴근까지 남은 N 시간과 각 일에 대한 작업량 works에 대해 야근 피로도를 최소화한 값을 리턴하는 함수 solution을 완성해주세요.

제한 사항

• works는 길이 1 이상, 20,000 이하인 배열입니다.
• works의 원소는 50000 이하인 자연수입니다.
• n은 1,000,000 이하인 자연수입니다.

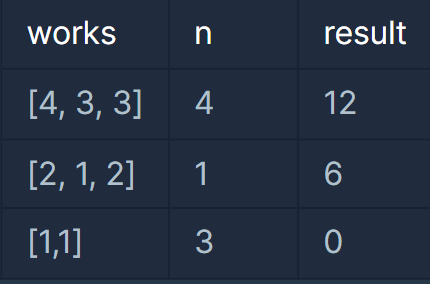
입출력 예

입출력 예 설명

입출력 예 #1

n=4 일 때, 남은 일의 작업량이 [4, 3, 3] 이라면 야근 지수를 최소화하기 위해 4시간동안 일을 한 결과는 [2, 2, 2]입니다. 이 때 야근 지수는 22 + 22 + 22 = 12 입니다.

입출력 예 #2

n=1일 때, 남은 일의 작업량이 [2,1,2]라면 야근 지수를 최소화하기 위해 1시간동안 일을 한 결과는 [1,1,2]입니다. 야근지수는 12 + 12 + 22 = 6입니다.

풀이

1. 이분탐색으로 해결할 수 있을 것 같았다...
2. begin은 1로, end는 works 원소의 총 합으로 설정했다
3. 그렇게 막대 자르기 식으로 범위를 좁혀나가다가 n이 딱 맞게 떨어지는 경우에는 그대로 계산해주었고
4. start가 end랑 같아지는 시점에는 배열을 정렬해놓고 남은 n에 대해서만 --를 수행해주었다.

이거 풀고나서 솔직히 좀 뿌듯해서 풀이를 찾아봤는데 절망적이었다.

다른 사람의 풀이는 정렬해놓고 최대값에서 --해줌을 반복했던 것이다.

내가 알기로는 Arrays.sort는 퀵정렬을 사용해서 이미 정렬된 데이터에 대해서는 시간복잡도가 O(n2)인데다가 문제 조건상 최악의 경우 --연산을 백만번을 수행하기때문에 효율성에서 당연히 걸릴 줄 알고 효율성 걱정없는 이분탐색을 애초에 선택했던 것인데 내가 멍청한 것이었다...

음.. 그래도 이분탐색 구현력을 좀 늘렸다는 것에 만족하자!

코드

import java.util.*;
class Solution {
    public long binary_search(int[] works, long start, long end, int n) {
        long mid = 0;
        long answer = 0;
        while(start < end) {
            mid = (start + end) / 2;
            long sum = 0;
            for(int i = 0; i < works.length; i++) {
                if(works[i] > mid)
                {
                    sum += (works[i] - mid);
                }
            }
            if(sum < n)
            {
                for(int i = 0; i < works.length; i++)
                    if(works[i] > mid)
                        works[i] = (int) mid;
                n -= sum;
                end = mid;
            }
            else if(sum > n)
            {
                start = mid + 1;
            }
            else {
                for(int i = 0; i < works.length; i++) {
                    if(works[i] > mid)
                        works[i] = (int) mid;
                    answer += works[i] * works[i];
                }
                return answer;
            }
        }
        Arrays.sort(works);
        for(int i = works.length - 1; i >= 0 && n > 0; ) {
            works[i]--;
            n--;
            if(works[i] < works[i - 1]) i--;
        }
        for(int i = 0; i < works.length; i++)
            answer += works[i] * works[i];
        return answer;
    }
    public long solution(int n, int[] works) {
        long answer = 0;
        long sum = 0;
        for(int i = 0; i < works.length; i++)
            sum += works[i];
        if(sum > n)
            answer = binary_search(works, 1, sum, n);
        return answer;
    }
}