링크

문제 링크

문제 설명

Finn은 편의점에서 야간 아르바이트를 하고 있습니다. 야간에 손님이 너무 없어 심심한 Finn은 손님들께 거스름돈을 n 원을 줄 때 방법의 경우의 수를 구하기로 하였습니다.

예를 들어서 손님께 5원을 거슬러 줘야 하고 1원, 2원, 5원이 있다면 다음과 같이 4가지 방법으로 5원을 거슬러 줄 수 있습니다.

• 1원을 5개 사용해서 거슬러 준다.
• 1원을 3개 사용하고, 2원을 1개 사용해서 거슬러 준다.
• 1원을 1개 사용하고, 2원을 2개 사용해서 거슬러 준다.
• 5원을 1개 사용해서 거슬러 준다.

거슬러 줘야 하는 금액 n과 Finn이 현재 보유하고 있는 돈의 종류 money가 매개변수로 주어질 때, Finn이 n 원을 거슬러 줄 방법의 수를 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• n은 100,000 이하의 자연수입니다.
• 화폐 단위는 100종류 이하입니다.
• 모든 화폐는 무한하게 있다고 가정합니다.
• 정답이 커질 수 있으니, 1,000,000,007로 나눈 나머지를 return 해주세요.

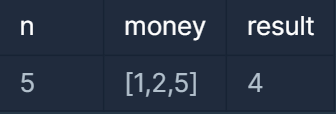
입출력 예

입출력 예 설명

입출력 예 #1
문제의 예시와 같습니다.

풀이

1. 조합으로 풀려했는데 리턴값이 100000007이 넘을 수 있다는 말을 보고 DP를 떠올리자!
2. DP 2차원 배열을 선언해서 행은 동전, 열은 n으로, 행까지의 동전으로 n을 만들 수 있는 경우의 수를 DP[i][j]로 정하자

이 문제를 처음에는 조합으로 풀려했다.

동전의 개수를 올려서 sum이 n이랑 같아질 때, answer++해주면서 일일이 개수를 셀려했는데 문제 제한사항에 1000000007로 나눈 나머지를 리턴하라고 하는것을 보고 좀 찝찝했다.

(근데 생각해보니 1000000007로 안나누고 리턴했는데 통과함..)

그래서 풀이법은 DP밖에 없다는 생각이 떠올랐다.

완탐이나 백트래킹으로 저 숫자를 넘길려면 무조건 시간초과였기 때문이다!

근데 DP로 풀려고 2차원배열을 선언해놓고 나니까 점화식을 어떻게 세워야할 지 모르겠더라,,

그래서 연습장에다가 2차원 배열의 DP를 처음에 손으로 풀어보고 점화식을 찾으려고 했다.

(고생의 흔적)

그렇게 보다보니 1원,2원으로 5원을 만들기 위해서는 1원으로 5원을 만들 수 있는 경우의 수 + dp[5 - (2원)]을 하니까 되는 것을 찾았다.

이는 1원,2원,5원을 가지고 n을 만들때도 동일한 규칙을 찾을 수 있었고 결국 이를 점화식으로 나타냈다.

코드

class Solution {
    static int [][] dp;
    public int solution(int n, int[] money) {
        int answer = 0;
        dp = new int[money.length][n + 1];
        for(int i = 0; i <= n; i++) {
            dp[0][i] = i % money[0] == 0 ? 1 : 0;
        }
        for(int i = 0; i < dp.length; i++)
            dp[i][0] = 1;
        for(int i = 1; i < dp.length; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j] = dp[i - 1][j];
                if(j >= money[i]) dp[i][j] += dp[i][j - money[i]];
            }
        }
        return dp[dp.length - 1][dp[0].length - 1];
    }
}