1.문제
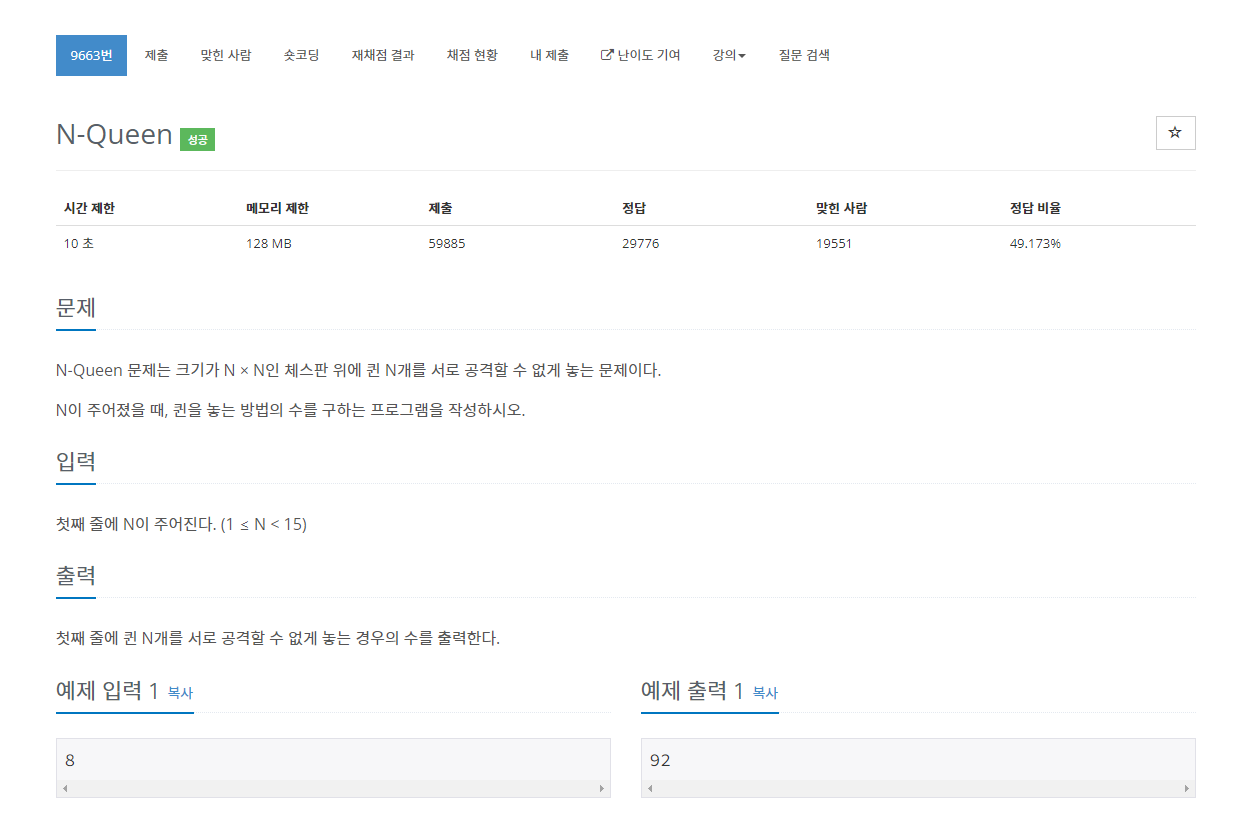
2.풀이
처음 문제를 풀때는 N * N만큼의 체스판을 2차원 배열로 선언하고 반복문을 돌면서 각각의 가로 세로 대각선을 검사하는 코드를 짜려고 했으나 대각선 코드를 짜는게 힘들기도 했고 메모리 문제로 좀 더 효율적인 접근을 하는 방법을 모색해야 했다.
그래서 검색을 한 결과 2차원 배열이 아닌 1차원 배열로 체스판을 구현하고 문제를 푸는 방법을 알게되어 이를 활용해 문제를 풀었다.
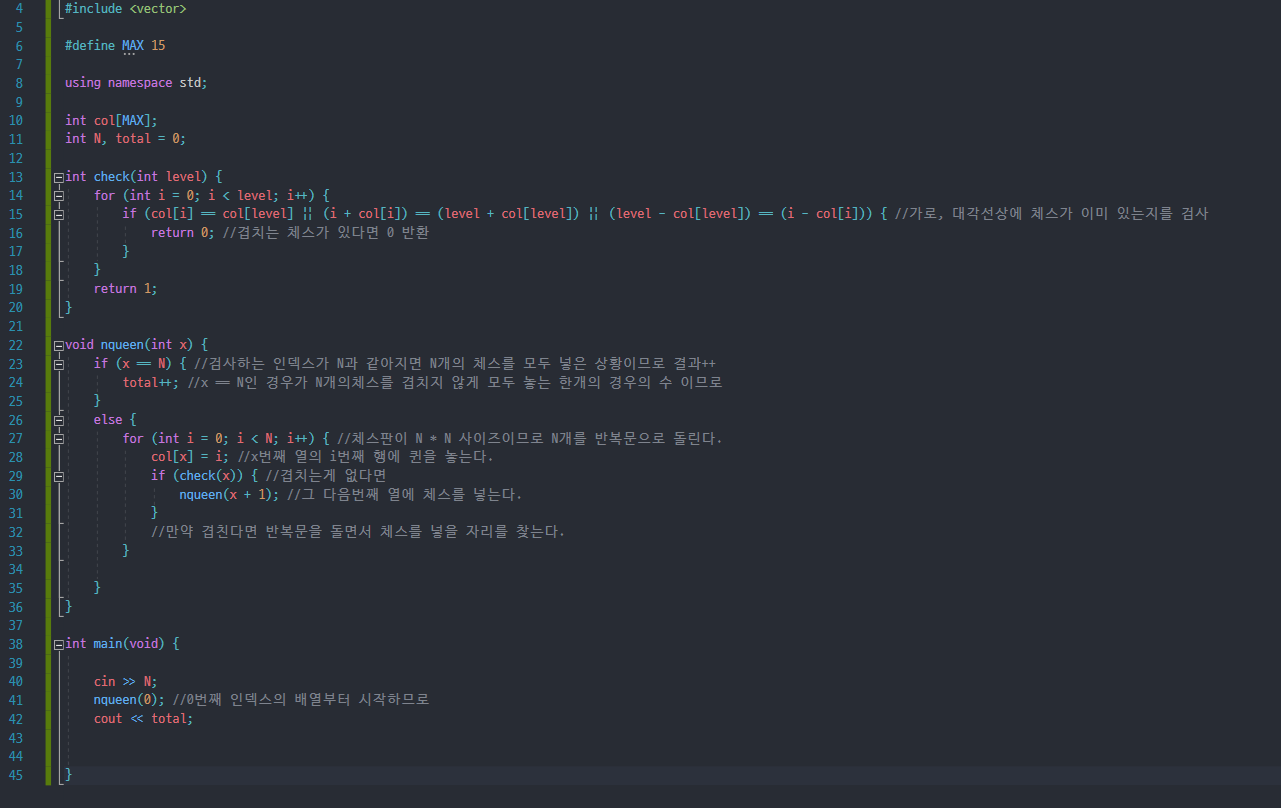
풀이 흐름도
- n개의 1차원 배열을 선언한다.
- 0번째 배열부터 시작하므로 nqueen에 0을 넣어 함수를 실행시킨다
- 만약 nqueen의 매개변수 x가 N과 같아지는 경우 모든 체스를 나열한 경우이므로 total++해준다.
- 0~N-1까지 for문을 돌면서 퀸을 두고 겹치는게 있는지 check를 통해 검사한다.
- 만약 check에서 true가 나온다면 겹치는 체스가 없다는 의미이므로 다음행으로 이동하기위해 nqueen(x + 1)을 실행해준다.
- total을 출력시킨다.
3.배운점
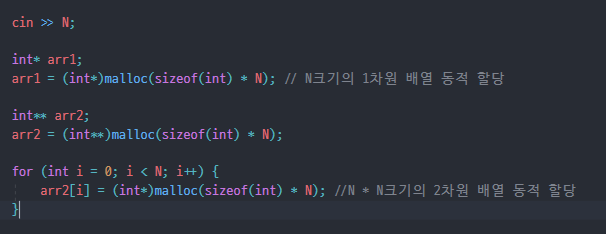
처음에 2차원 배열을 만드는 과정에서 2차원배열의 동적 할당에 대해 배우게 되었다.
동적 1차원, 2차원 배열 만드는 방법
대각선 법칙 1
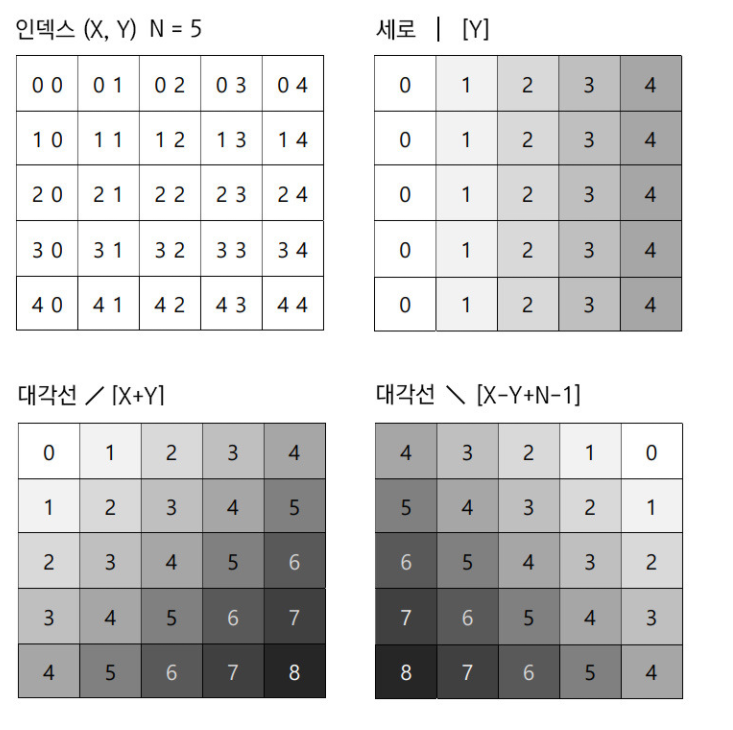
대각선 법칙 2
(X, Y)의 대각선에 위치한 좌표 (A, B)에서 반드시 X-A = Y-B를 만족한다.
예를 들어 (0 , 1)을 기준으로 했을때, 대각선에 있는 점들 (1, 2) (2, 3) 은 반드시
(0 - 1) = (1 - 2) = -1, (0 - 2) = (1 - 3) = -2를 만족한다는 것이다.
