백준문제

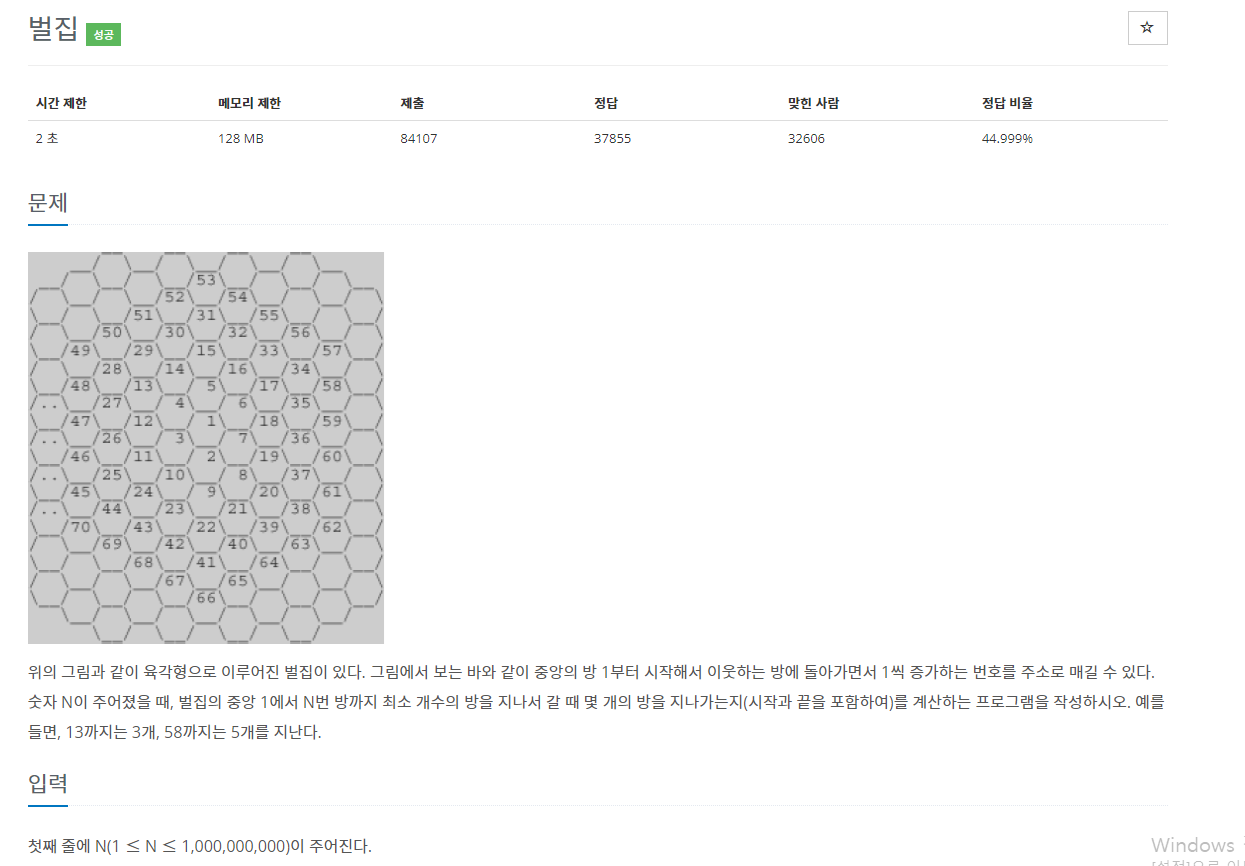
육각형의 테두리가 한칸씩 늘어날 때 마다 거쳐야하는 횟수도 한개씩 증가한다는 점에 착안해서 문제를 풀었다.예를 들어 두번째 테두리인 2~7은 두번 세번째 테두리인 8~19는 세번 거쳐야 찾을수 있다.이때, 각 테두리의 시작숫자는 이전 테두리 시작숫자에서 6, 12 18

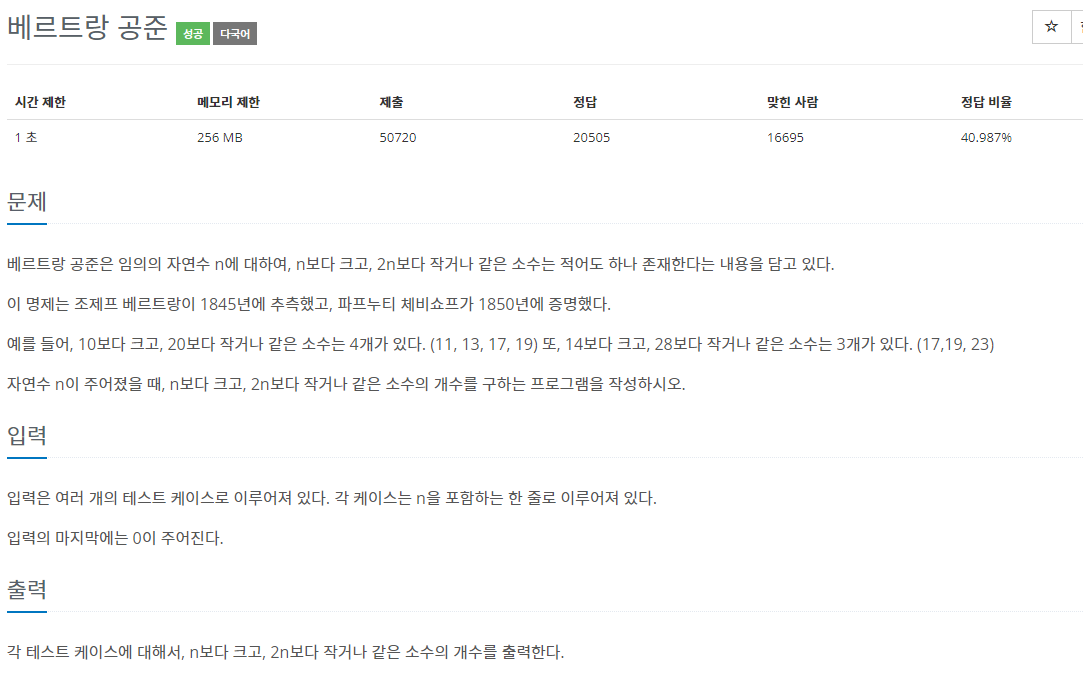
에라토스테네스 체를 이용해서 문제를 풀었다. 에라토스네테스의 체는 소수를 구하는 알고리즘으로 이중포문을돌려 특정 숫자를 해당 숫자 이하의 모든숫자로 나누는(좀더 시간을 줄이려면 제곱근 이하의 숫자로 나누면됨) 경우보다 훨씬 적은 시간에 소수들을 찾아 낼 수 있다.원리는

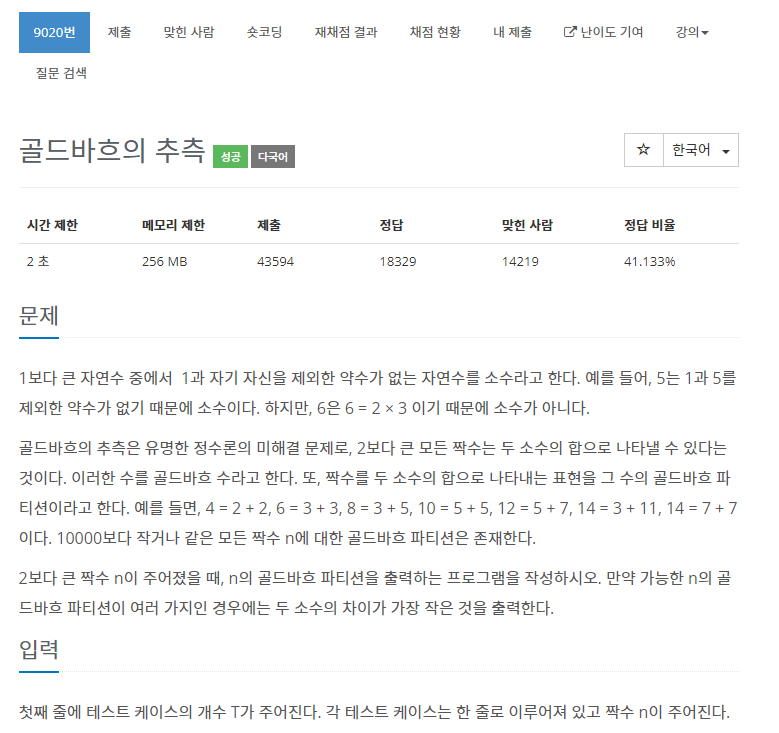
처음 문제를 풀었을때는 에라토스테네스의 체를 통해 소수를 구하는 과정을 while문 안에 넣어 테스트 케이스마다 반복되게 코드를 짜서 시간초과오류를 받았고, 그래서 밖으로 뺏지만 그래도 여전히 오류가 났다.그래서 시간을 줄이기 위해 생각해보니 이중포문에서 시간을 많이

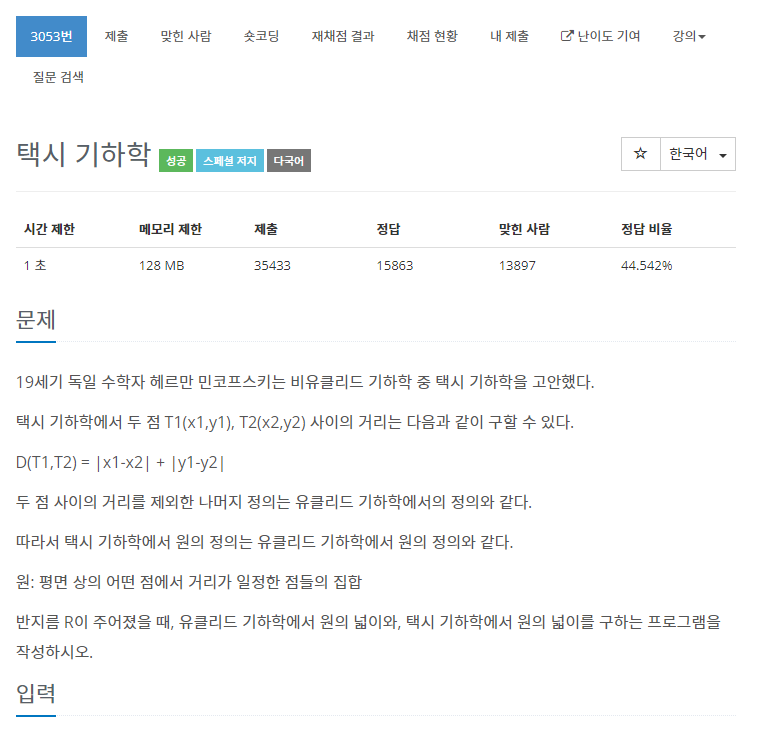
우리가 흔히 하는 유클리드 기하학에서 원이라 함은 한점에서부터 다른한점까지의 거리가 모두 일정한 선들의 집합을 뜻한다. 여기서 한점과 다른 한 점 사이의 거리는 다음과같다. 즉 첫번째 사진의 초록색 선을 유클리드기하학에서 구한 두점사이의 거리이다.택시기하학의 경우 이동

정렬 알고리즘 중 삽입정렬을 활용해 문제를 풀었다.삽입정렬은 우리가 무작위의 카드를 다시 정렬하는 방법과 같다.1번인덱스가 0번 인덱스보다 작다면 왼쪽 아니면 그대로2번인덱스가 1번인덱스보다작다면 왼쪽 아니면 그대로2.1 2번인덱스가 1번인덱스보다 작고 0번보다 작다면

처음에는 map을 활용하여 문제를 풀었고, 풀이는 다음과 같다n개의 숫자를 받아 tmp배열과 map에 각각 따로 저장한다.map은 자동 정렬이 되므로 map의 처음과 끝을 돌며 앞에 몇개의 숫자가 있는지 index 변수로 세어주고 각 key값의 value쌍으로 넣어준

1.문제 2.풀이 처음 문제를 풀때는 N * N만큼의 체스판을 2차원 배열로 선언하고 반복문을 돌면서 각각의 가로 세로 대각선을 검사하는 코드를 짜려고 했으나 대각선 코드를 짜는게 힘들기도 했고 메모리 문제로 좀 더 효율적인 접근을 하는 방법을 모색해야 했다. 그래

빈칸(0)에만 숫자를 넣고 유효성 검사를 해야하므로 빈칸의 인덱스를 배열에 기록해둔다.1-1.이를 위해 좌표쌍을 가진 point라는 int형 pair를 선언, points라는 배열에 넣어준다.cnt변수에 0의 갯수를 기록해둔뒤, 재귀함수를 돌때마다 size변수의 크기를