[자료구조] 트리의 개념과 이진트리(Binary Tree)

아는벌·2023년 2월 8일
자료구조
0

자료구조

목록 보기
5/8
post-thumbnail

트리

배열이나 연결리스트의 단점

1) 데이터를 일렬로 저장하기 때문에 탐색 연산이 순차적으로 수행되어야 함
2) 배열은 미리 정렬해놓으면 이진탐색을 통해 효율적인 탐색이 가능하지만 삽입이나 삭제 후에도 정렬 상태를 유지해야 하므로 삽입이나 삭제하는데 O(N) 시간 소요
이러한 문제점을 보완한 계층적 자료구조 => 트리

트리의 개념

실제 트리를 거꾸로 세워 놓은 형태의 자료구조
하나 이상의 노드로 이루어진 유한집합

트리는 empty이거나, empty가 아니면 루트노드 R과 트리의 집합으로 구성되는데 각 트리의 루트노드는 R의 자식 노드이다. 단, 트리의 집합은 공집합일 수도 있다.

응용

(1) HTML, xml의 문서 트리
(2) 자바 클래스 계층구조
(3) 운영체제의 파일시스템
(4) 탐색트리(Search Tree), 힙(Heap) 자료구조, 컴파일러의 수식을 위한 구문트리(Syntax Tree) 등의 기본이 되는 자료구조

용어

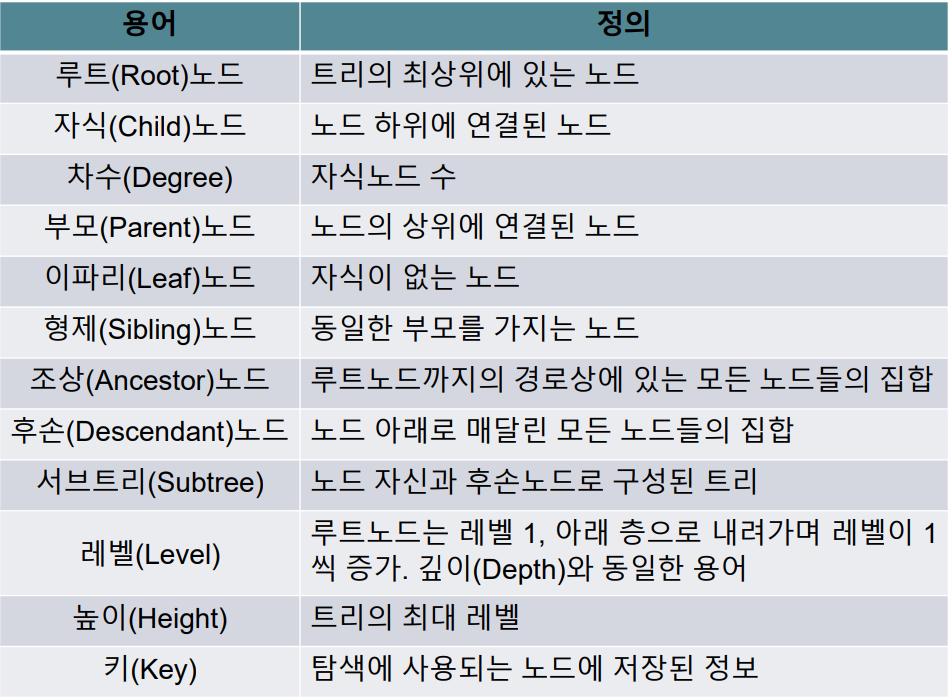
1) 하나의 루트 노드
2) 나머지 노드들은 n(>=0)의 분리 집합 T_1, T_2, ... , T_n으로 분할(T_i : 루트의 서브트리)
3) node: 한 정도 아이템 + 다른 노드로 뻗어진 가지
4) 노드의 차수(degree) : 노드의 서브트리 수
5) 트리의 차수 = max(노드의 차수)
6) 단말(Termianl) 노드 / 외부(External) 노드 : leaf node의 다른 말
7) 비단말(Non-Terminal) 노드 / 내부(Internal) 노드 : 이파리가 아닌 노드
8) 일반적인 트리를 메모리에 저장하려면 각 노드에 키와 자식 수만큼의 레퍼런스 저장 필요

예제

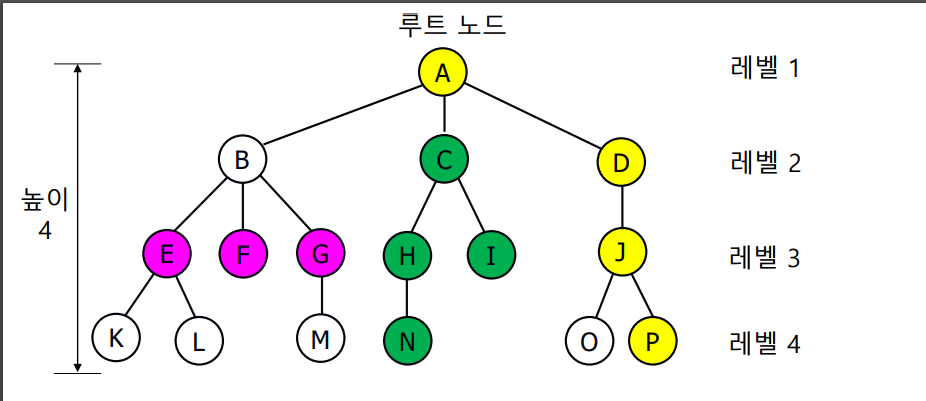
  • 트리 height: 4
  • A : 트리의 루트 노드
  • B, C, D : 각각 A의 child 노드
  • A의 차수 : 3
  • B, C, D의 부모 노드 : A
  • C의 descendent : {H, I, N}
  • K, L, F, M, N, I, O, P : leaf nodes
  • E, F, G는 서로 형제 노드
  • P의 조상 노드 : {J, D, A}

특성

  • N개의 노드가 있는 최대 차수가 k인 트리
    - null 레퍼런스 수 = Nk - (N-1) = N(k-1)+1
    • Nk = 총 레퍼런스의 수
    • (N-1) = 트리에서 부모-자식을 연결하는 레퍼런스 수
  • K 가 클수록 메모리 낭비가 심해짐
  • -> 트리 탐색 과정에서 null 레퍼런스를 확인해야 하므로 시간적으로 비효율적

왼쪽자식-오른쪽형제 표현

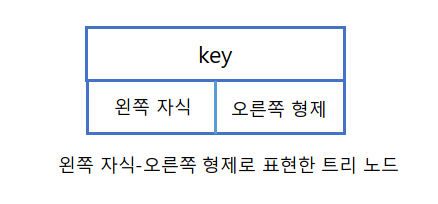
왼쪽자식-오른쪽형제(Left Child-Right Sibling) 표현은 이러한 단점을 보안해주는 자료구조로 노드의 왼쪽 자식과 왼쪽 자식의 오른쪽 형제노드를 가리키는 2개의 레퍼런스만을 사용한다.

이진트리

개념

이진트리(Binary Tree) - 각 노드의 자식 수가 2 이하인 트리

이진트리는 empty이거나 empty가 아니면, 루트노드와 2개의 이진트리인 왼쪽 서브트리와 오른쪽 서브트리로 구성됨

컴퓨터 분야에서 널리 활용되는 기본적인 자료구조

  • 이진트리가 데이터의 구조적인 관계를 잘 반영하고, 효율적인 삽입과 탐색을 가능하게 하며, 이진트리의 서브트리를 다른 이진트리의 서브트리와 교환하는 것이 용이함

이진트리의 예


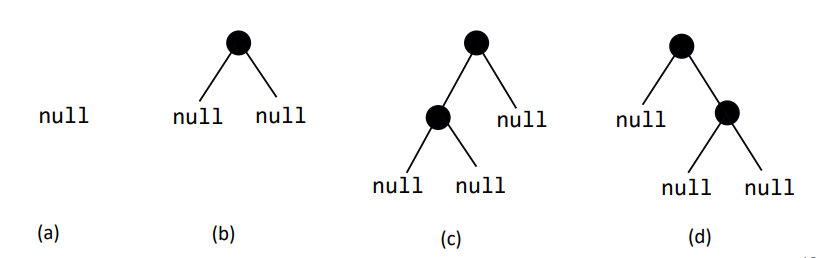
(a) - empty인 트리
(b) - 루트노드만 있는 이진트리
(c) - 루트노드의 오른쪽 서브트리가 없는(empty) 이진트리
(d) - 루트노드의 왼쪽 서브트리가 없는 이진트리

특별한 형태의 이진트리

1) 포화이진트리(Full Binary Tree)
: 모든 이파리노드의 깊이가 같고 각 내부노드가 2개의 자식노드를 가지는 트리

2) 완전이진트리(Complete Binary Tree)
: 마지막 레벨을 제외한 각 레벨이 노드들로 꽉 차있고, 마지막 레벨어는 노드들이 왼쪽부터 채워진 트리, 포화이진트리는 완전이진트리이다.

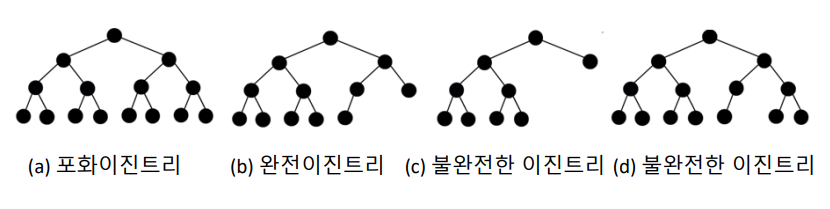
(a) - 포화이진트리
(b) - 완전이진트리
(c) - 레벨 3에 노드들이 채워져 있지 않다
(d) - 마지막 레벨에 노드들이 왼쪽부터 꽉 채워져 있지 않다

특징

  • 레벨 k에 있는 최대 노드 수 = 2^(k-1) (단, k=1,2,3...)
  • 높이가 h인 포화이진트리에 있는 노드 수 = 2^h - 1
  • N개의 노드를 가진 완전이진트리의 높이 = [ log_2(N+1) ]

구현

배열을 이용한 이진 트리

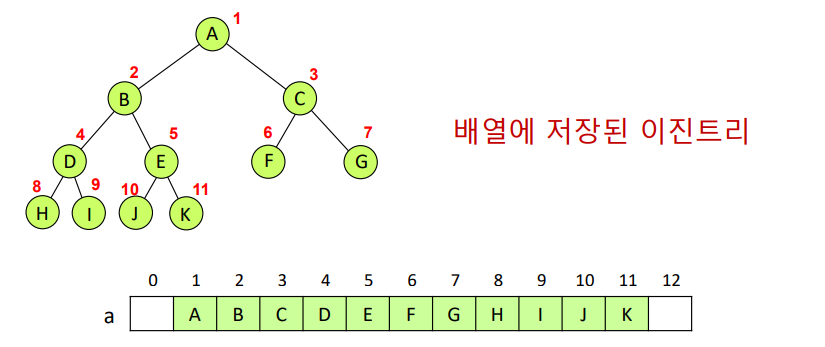
  • a[i]의 부모노드는 a[i/2]에 있다 (단, i > 1)
  • a[i]의 왼쪽 자식노드는 [2i]에 있다 (단, 2i <= N)
  • a[i]의 오른쪽 자식노드는 a[2i+1]에 있다 (단, 2i+1 <= N)

편향 이진 트리


완전이진트리를 배열을 사용해 저장하는 경우, 레퍼런스를 저장할 메모리 공간이 필요가 없어 매우 효율적이다. 하지만 편향(Skewed) 이진트리를 배열에 저장하는 경우, 트리의 높이가 커질 수록 메모리 낭비가 심하다.

재귀 구조를 이용한 트리

이진트리의 노드는 키와 left, right를 가지는 이진트리의 노드로 구현

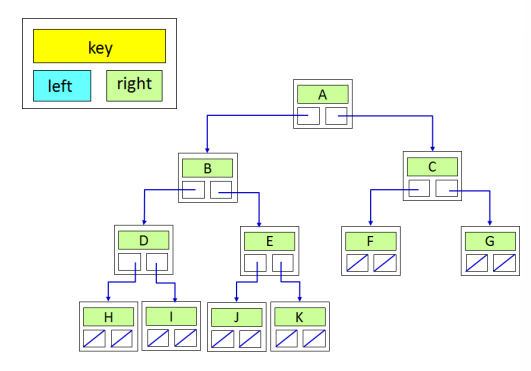
node 클래스

public class Node  <Key extends Comparable<Key>>{
    private Key item;
    private Node<Key> left;
    private Node<Key> right;
    public Node(Key newItem, Node lf, Node rt){
        item = newItem;
        left = lf;
        right = rt;
    }
    // get, set 메소드
 }

Binary Tree 클래스

public class BinaryTree <Key extends Comparable<Key>> {
    private Node root;
    public BinaryTree() { root=null; }
    public Node getRoot() { return root; }
    public void setRoot(Node root) { this.root = root; }
    public boolean isEmpty() { return root==null;}
    // 순회 연산 메소드
    // size(), height(), isEqual() 메소드
}

이진트리의 연산

이진트리에서 수행되는 기본 연산들은 트리를 순회하며 진행

전위순회 (Preorder Traversal)

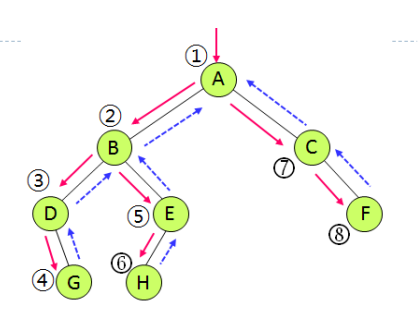
  • 노드 x에 도착했을 때 x를 먼전 방문
  • x의 왼쪽 자식노드로 순회를 계속
  • 왼쪽 서브트리의 모든 노드 방문 후에 오른쪽 서브트리의 모든 후손 노드들을 방문
  • NLR / VLR 순서
    public void preorder(Node node){
        if(node != null) {
            System.out.println(node.getKey()+" ");  // node 방문
            preorder(node.getLeft());
            preorder(node.getRight());
        }
    }

중위순회 (Inorder Traversal)

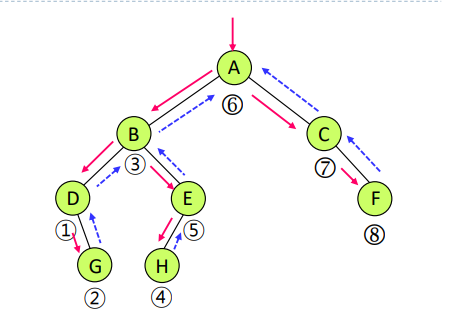
  • 노드 x에 도착하면 x의 방문을 보류하고 x의 왼쪽 서브트리로 순회를 먼저 진행
  • 왼쪽 서브트리의 모든 노드들을 방문한 후에 x 방문
  • x를 방문한 후에 x의 오른쪽 서브트리를 같은 방식으로 방문
  • LNR / LVR 순서
    public void inorder(Node node){
        if(node != null){
            inorder(node.getLeft());
            System.out.println(node.getKey()+" ");
            inorder(node.getRight());
        }
    }

후위순회 (Postorder Traversal)

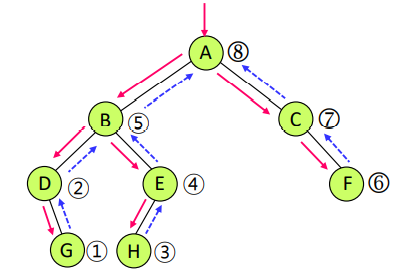
  • 노드 x에 도착하면 x의 방문을 보류하고 x의 왼쪽서브트리로 순회를 먼저 진행
  • x의 왼쪽 서브트리 모두 방문 후에 x의 오른쪽 서브트리를 방문
  • 마지막으로 노드 x 방문
  • LRN / LRV 순서
    public void postorder(Node node){
        if(node != null){
            postorder(node.getLeft());
            postorder(node.getRight());
            System.out.println(node.getKey()+" ");
        }
    }

레벨순회 (Level order Traversal)

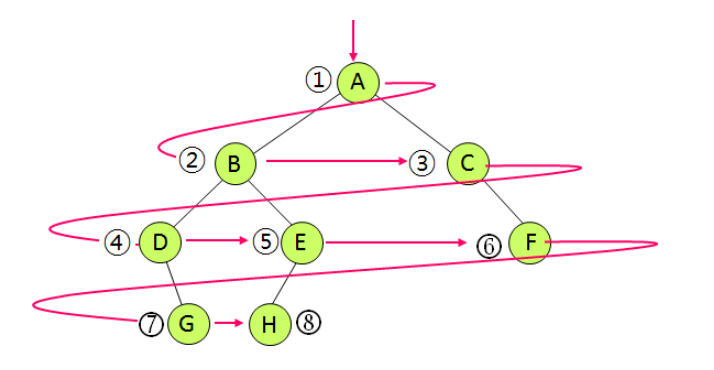
  • 루트노드가 있는 최상위 레벨부터 시작하여 각 레벨마다 좌 -> 우로 노드들을 방문
    public void levelorder(Node root){
        Queue<Node> q = new LinkedList<Node>(); // 큐 자료구조 이용
        Node t;
        q.add(root);    // 루트 노드 큐 삽입
        while(!q.isEmpty()){
            t = q.remove(); // 큐에서 가장 앞에 있는 노드 제거
            System.out.println(t.getKey()+" "); // 제거된 노드 출력(방문)
            if(t.getLeft()!=null)
                q.add(t.getLeft()); // 큐에 왼쪽 자식 삽입
            if(t.getRight()!=null)
                q.add(t.getRight());    // 큐에 오른쪽 자식 삽입
        }
    }

트리의 노드 수

트리의 노드 수
= 1 + (루트노드의 왼쪽 서브트리에 있는 노드 수) + (루트노드의 오른쪽 서브트리에 있는 노드 수)

   public int size(Node n){    // n을 루트로하는 (서브)트리에 있는 노드의 수
        if(n == null)
            return  0;
        else
            return (1 + size(n.getLeft()) + size(n.getRight()));
    }

트리의 높이

트리의 높이
= 1 + max(루트의 왼쪽 서브트리의 높이, 루트의 오른쪽 서브트리의 높이)

    public int height(Node n){    // n을 루트로하는 (서브)트리의 높이
        if(n == null)
            return  0;
        else
            return (1 + Math.max(height(n.getLeft()),height(n.getRight())));
    }

이진트리 비교

  • 전위순회 과정에서 다른 점이 발견되는 순간 false 리턴
    public static boolean isEqual(Node n , Node m) {    // 두 트리의 동일성 검사
        if(n == null || m == null)
            return n == m;
        if(n.getKey().compareTo(m.getKey()) != 0)   // 둘 다 null이 아니면 item 비교
            return false;
        return (isEqual(n.getLeft(),m.getRight()) &&    // item이 같으면 왼쪽/오른쪽 자식으로 재귀호출
                isEqual(n.getRight(),m.getLeft()));
    }

수행시간

  • 위 연산들은 트리의 각 노드를 한 번씩만 방문하므로 O(N) 시간 소요됨
profile
아는벌
이전 포스트

[자료구조] 큐(Queue)의 기본 개념과 구현

다음 포스트

[자료구조] 트리 Union-Find 연산

0개의 댓글