[자료구조] 트리 Union-Find 연산

아는벌·2023년 2월 12일

자료구조

목록 보기

6/8

상호배타적 집합을 위한 트리 연산

집합에 관련된 연산
1) union 연산 - 2개의 집합을 하나의 집합으로 만드는 연산
2) find 연산 - 주어진 원소에 대해 어느 집합에 속해 있는지 계산하는 연산, 루트를 찾는 연산
상호배타적 집합(Disjoint Set) - 어느 두 집합도 중복된 원소를 갖지 않는 집합들
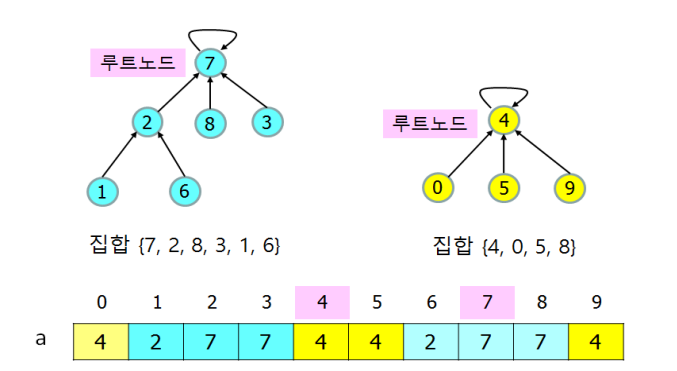
상호배타적 집합들을 메모리에 저장하기 위해 1차원 배열 사용
원소들을 0, 1, 2, ... ,N-1로 놓으면 이를 배열의 인덱스로 활용
집합에 속한 원소들 사이에 특정한 순서가 없고, 또 중복된 원소도 없음

Union 연산

rank에 기반하여(union-by-rank) rank가 높은 루트가 union 후에도 승자(합쳐진 트리의 루트)가 되도록 함
-> 두 트리가 하나로 합쳐진 후에 트리의 높이가 커지는 것을 방지하기 위해

ex) union(7, 4) 수행

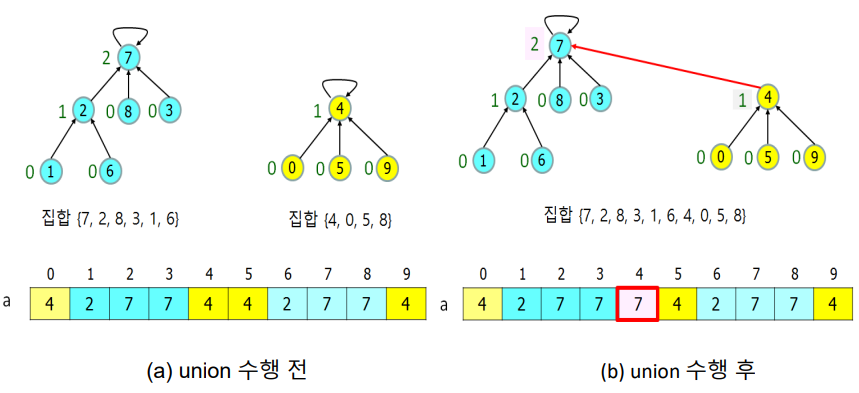
a[7] = 7로 갱신되어있고 트리도 하나로 합쳐짐

Find 연산

루트노드까지 올라가는 경로 상의 각 노드의 부모노드를 루트로 갱신한다 => 경로압축(Path Compression)

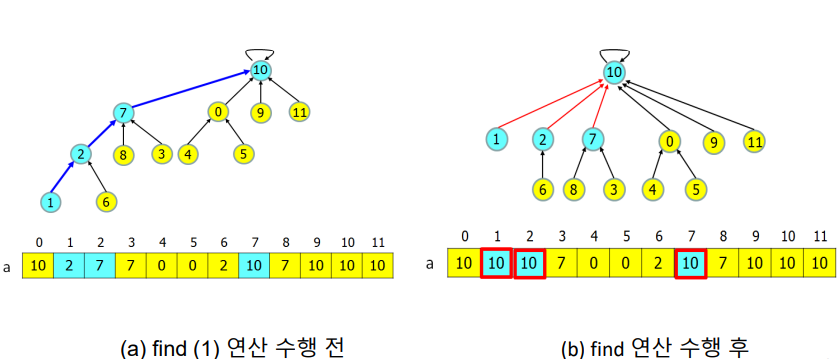
(a) find(1)을 수행하면 루트인 10까지 올라가는 경로 상의 모즌 노드 1, 2, 7의 부모노드를 10으로 갱신하여 (b)와 같은 트리를 만든다.
경로압축은 당장의 find(1) 연산의 수행시간을 줄이지는 않으나, 추후의 find(1), find(2) 연산의 수행시간을 단축함
경로압축으로 인해 루트의 rank는 트리의 높이와 달라질 수 있음

구현

상호배타적 집합을 위한 Node 클래스

public class Node {
    int parent;
    int rank;
    // 생성자
    public Node(int newParent, int newRank){
        parent = newParent;
        rank = newRank;
    }
    // get, set
}

UnionFind 클래스

public class UnionFind {
    protected Node[] a;
    // 생성자
    public UnionFind(Node[] iarray){
        // Node 객체를 원소로 하는 1차원 배열을 가짐
        a = iarray;
    }
    // find()
    // union()

// 경로압축
// i가 속한 트리의 루트 노드를 재귀적으로 찾고 최종적으로 경로상의 각 원소의 부모를 루트노드로 만듦
    protected int find(int i){
        if(i!=a[i].getParent())
            // 리턴하며 경로상의 각 노드의 부모가 루트가 되도록 만듦
            a[i].setParent(find(a[i].getParent()));
        return a[i].getParent();
    }

i가 속한 트리의 루트를 리턴하는 동시에 노드 i에서 루트까지의 경로상의 모든 노드들에 대한 부모노드를 루트로 갱신하는 경로압축 수행한다.
find(a[i].getParent())의 값이 재귀적으로 호출되며 계속 루트노드로 리턴되어 경로 상의 각 노드 i의 parent가 동일한 루트로 갱신된다.

  // union 연산
    public void union(int i, int j){
        // i가 속한 트리와 j가 속한 트리의 루트 찾기
        int iroot = find(i);
        int jroot = find(j);
        // 두 루트노드가 동일하다면 union 수행없이 그대로 리턴
        if(iroot == jroot) return;

        //rank 비교 (rank가 높은 루트가 작은 rank를 가진 루트의 부모노드로 대체)
        if(a[iroot].getRank() > a[jroot].getRank())
            a[jroot].setParent(iroot);
        else if(a[iroot].getRank() < a[jroot].getRank())
            a[iroot].setParent(jroot);
        else{   // 두 루트의 rank가 같은 경우
            a[jroot].setParent(iroot);  // 둘 중 하나를 임의로 승자로
            int t = a[iroot].getRank() + 1;
            a[iroot].setRank(t);    // rank +1 증가
        }
    }

i가 속한 트리와 j가 속한 트리의 루트를 find 연산을 통해 찾고 각각의 루트노드를 iroot, jroot라고 한다. 두 루트노드가 동일하다면 union 연산을 수행하지 않고 그대로 리턴한다. 두 루트노드가 다르다면 두 트리의 rank를 비교한다. 비교 결과, 더 큰 rnak를 가지는 트리가 더 작은 rank를 가진 트리의 루트 노드의 부모 노드로 대체된다. 이 때 rank는 승자의 rnak를 그대로 가진다. 만일 두 루트가 같은 rank를 가진다면 둘 중 하나를 임의로 승자로 결정하여 한 루트가 다른 루트의 부모노드로 대체되고 rank는 1이 증가된다.

수행시간

union 연산 : 두 루트노드들을 각각 찾는 find 연산 수행 후 rank를 비교하여 승자가 합쳐진 트리의 노트를 담음, find() 연산을 제외한 순수 union 연산의 수행시간은 O(1) 시간
find 연산 : 최대 트리의 높이만큼 올라가야하므로 트리의 높이에 비례, find 연산을 수행하며 경로압축을 하므로 경로상의 노드에 대해 추후에 수행되는 find 연산의 수행시간은 트리의 높이보다는 적게 소요된다.
상각분석: O(N)번의 find와 union 연산들을 수행하여 걸린 총 시간을 연산 횟수로 나누어 1회의 연산 수행시간을 계산하면 1회의 find 연산의 수행시간은 O(logN)이다.