GAN

눈문링크: 링크텍스트

코드링크: 링크텍스트

Preview

1. 확률 분포

• 정의: 확률 변수가 특정한 값을 가질 확률을 나타내는 함수

1-1. 이산확률분포

• 정의: 확률 변수 X의 개수를 정확히 셀 수 있는 것.

1-2. 연속확률분포

• 정의: 확률 변수 x의 개수를 정확히 셀 수 없는 것(확률 밀도 함수로 표현)

• 예시: 정규분포(실제 세계에서 많은 데이터표현)

1-3. 이미지 데이터에 대한 확률 분포

• 이미지는 다차원 특징 공간의 한 점

  • 이미지의 분포를 근사하는 모델 학습 가능

• 통계적인 평균치가 존재

  • 모델은 이를 수치적 표현 가능

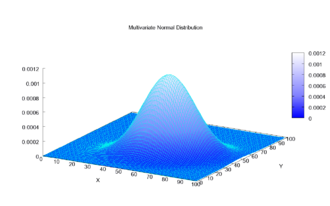
• 이미지에서의 다양한 특징들이 각각의 확률 변수가 되는 분포

  • 다변수 확률 분포

  

2. 생성모델(Generatinve Models)

• 정의: 실존하지 않지만 있을 법한 이미지 생성가능한 모델

• 특징:

  • 통계적 모델이다

  • 새로운 데이터의 인스턴스를 형성하기 위한 아키텍처이다

• 목표

  • 이미지 데이터의 분포를 근사하는 모델 G만든다

  • 모델 G가 작동을 잘한다는 것은 원래 이미지들의 분포 모델링 잘함

모델G

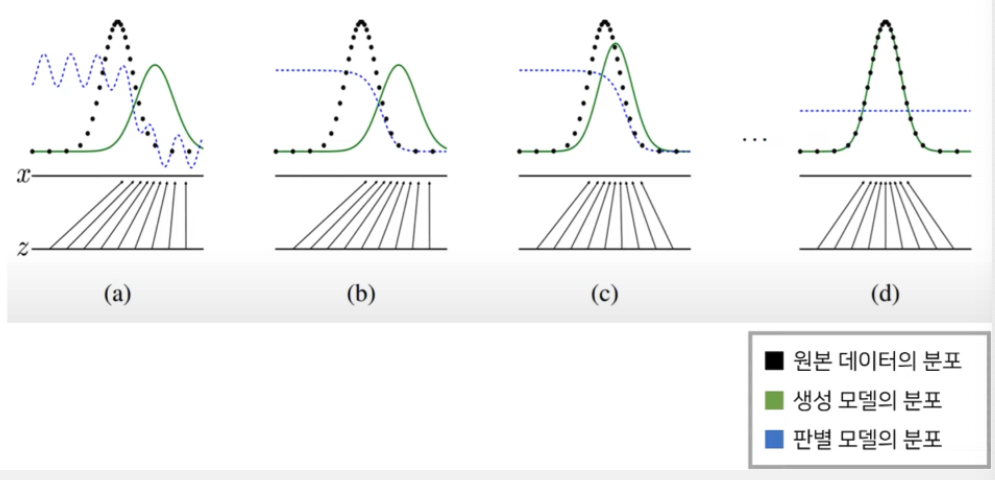
• 원래 데이터의 분포 근사 능력 학습

• 시간이 지나면서 원본 데이터의 분포를 학습

  • 학습이 잘 되었다면 통계적으로 평균 특징 가진 데이터 생성

GAN

• 특징

  • 생성자와 판별자 두 개의 네트워크 활용
  • 목적함수를 통해 생성자는 이미지 분포 학습

- Generator -- G(z): New data instance
 
- Discriminator --D(x)= Proability(Real:1 ~ Fake:0)

• 기댓값 계산 방법

  : 모든 데이터를 하나씩 확인하여 식에 대입한 후 평균 계산

  • Ex~pdata(x)[logD(x)]

    : 원본 데이터 분포에서 샘플 x를 뽑아 logD(x)의 기댓값 게산
    

  • Ez~pz(z)[log(1-D(G(z)))]

    : 노이즈 분포에서 샘플 z를 뽑아서 log(1-D(G(z)))의 기댓값 계산

• 기댓값 공식

  : 모든 사건에 대해 확률을 곱한 후 더해서 계산

  • x: 사건
  • f(x): 사건에 따른 확률
    *이산확률변수

  

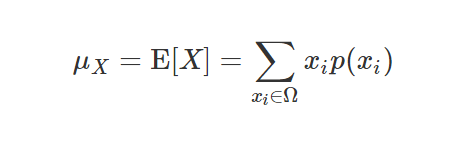
  *연속확률 변수 공식

  

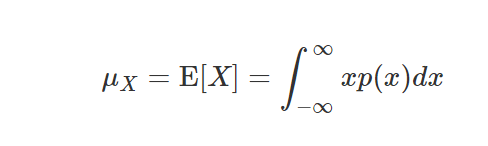
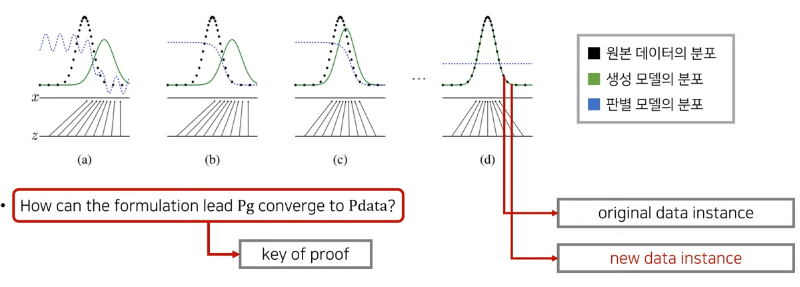
• GAN 수렴 과정

  • 공식 목표

    : Pg->Pdata, D(G(z)) -> 1/2

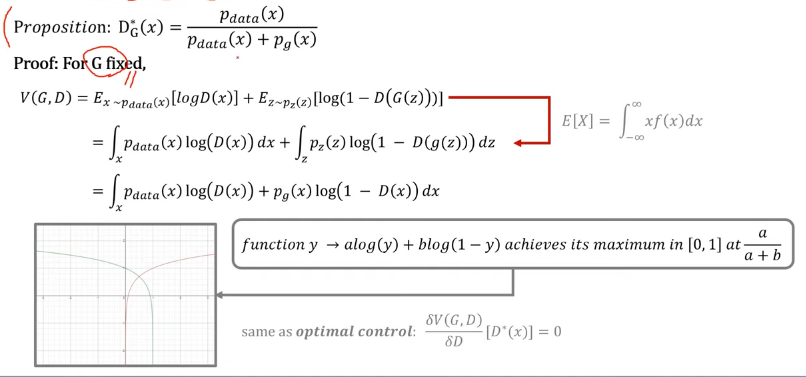
• 증명

  • Global Optimality

  

  

• GAN 알고리즘

  • for the number of training iterations do

    • for k steps do

      • Sample minibatch of m noise samples from noise prior pg(z).

      • Sample minibatch of m examples from data generating distribution p data(x).

      • Update the discriminator by ascending its stochastic gradient

      

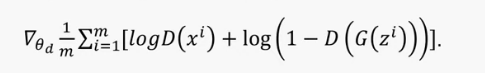
    • end for

      • Sample minibatch of m noise samples from noise prior pg(z)
      • Update the generator by descending its stochastic gradient

      

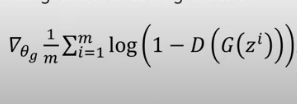
    • end for

      • The gradient-based updates can use any strandard gradient-based learning rule. They used momentum

Visualization of Experiment

• Not cherry- picked

• Not memorized the training set

• Competitive with the better generative models

• Images represent sharp