목적
How to calculate analytic gradient by 임의의 복잡한 함수.
Computatioal graph 프레임 워크 사용
-특징
:같은 종류의 그래프를 이용해서 아무 함수나 표현이 가능하다
: 그리고 그래프의 각 노드는 연산 단계를 말한다.
:backpropagation사용 가능
-역전파이다.
-gradient를 얻기 위해 chain rule을 재귀적으로 사용.
EX1 - (input:x,W인 선형 classifier)
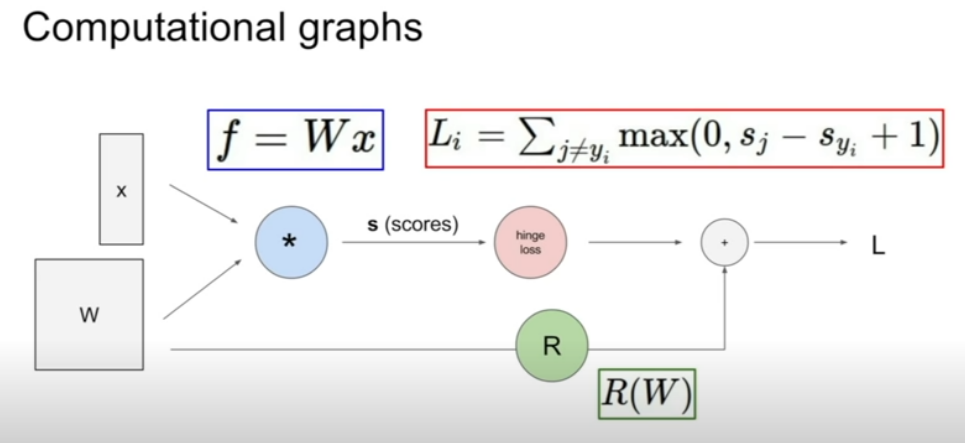
-score vector = W*x
-hingle loss = 데이터항 Li계산
-R : regularization항 계산
-L (최종 loss): regularization항 과 데이터 항의 합.
EX2 - Convolutional network(AlexNet)
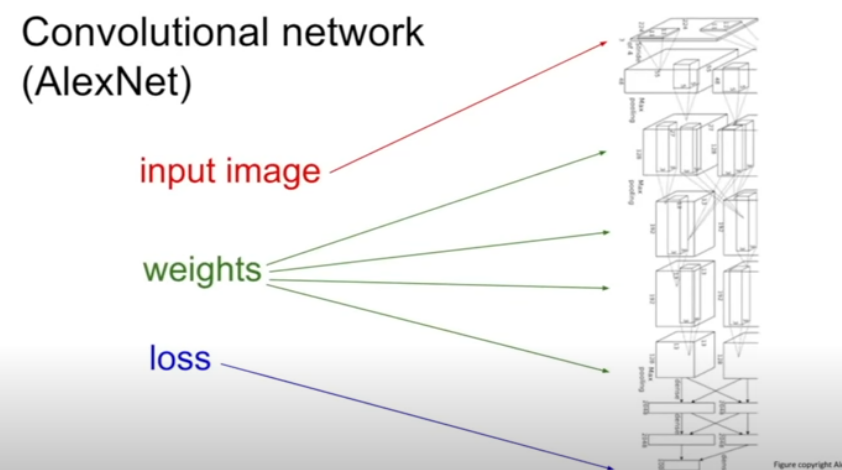
:입력이미지(top) -> loss(bottom)
이때, 무수히 많은 layer를 거쳐서 간다
EX3 - Neural Turing Machine
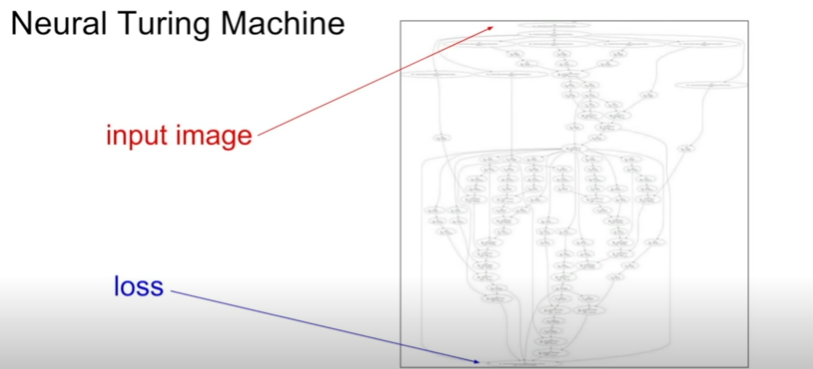
Backpropagation
스칼라의 경우
:많은 수학적 지식과 각 노드에서 단순한 gradient를 얻고 싶어하는 사이에서 간단한 그래프를 그릴 수 있고 그로 인해 복잡한 computaional graph
-목표: function f의 출력에 대해 어떤 변수 gradient 찾기 원함
-단순한 예시
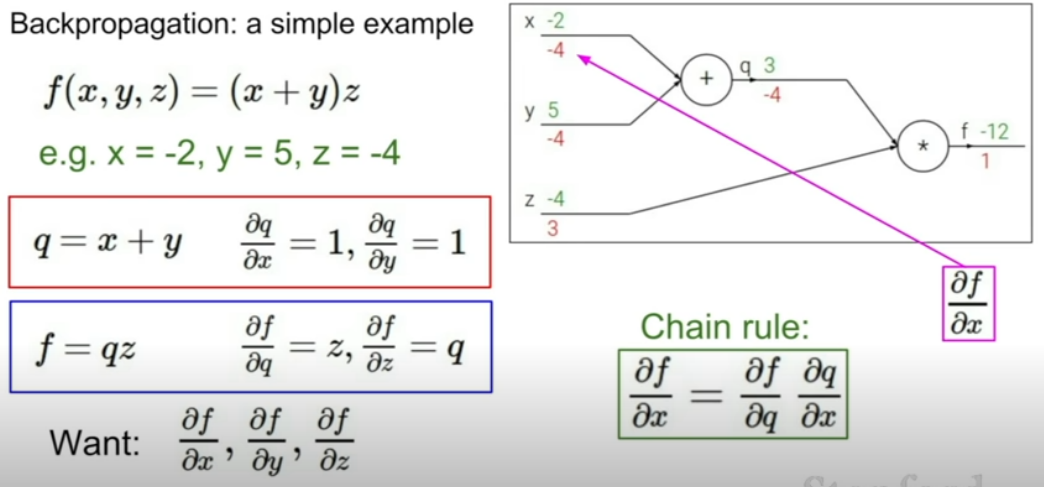
-조금 더 복잡한 예시

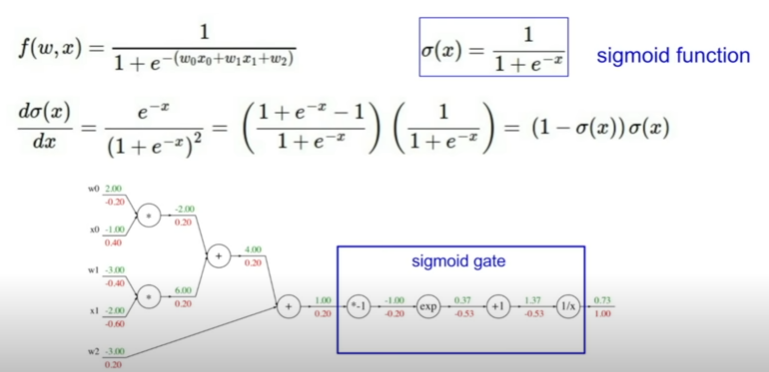
-sigmoid함수 예시
:local gradient를 통해 더 복잡한 노드 그룹 만들 수 있다.
: trade -off관계
-flow
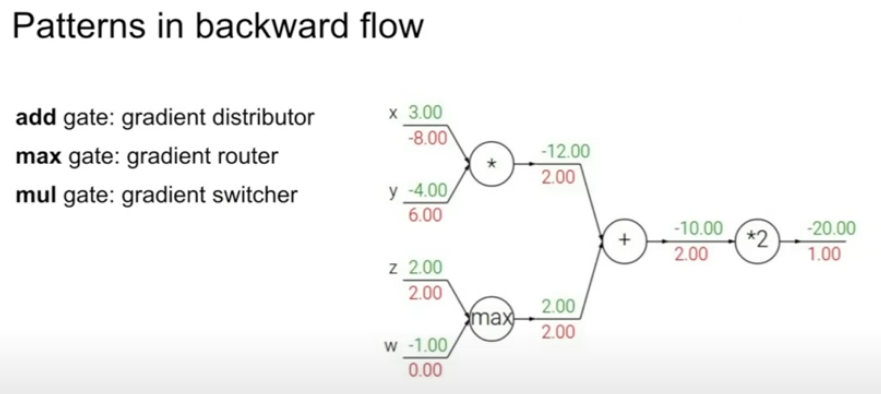
+add gate: gradient를 나눠준다
+max gate: 최댓값인 부분에는 gradient가 가고 그렇지 않은 부분은 0으로 되므로 gradient의 통로이다. 최댓값인 부분은 함수 계산에 실제로 영향을 주므로 어디를 조정하고 계산의 해당지점을 통해 흐르게 해야하는 곳
+mul gate: upstream gradient를 받아 다른 브랜치의 값으로 스켈링하는 gradient 스위처입니다.
-함수가 변수를 찾는 과정.(복잡한 함수에 대해 gradient 찾기)
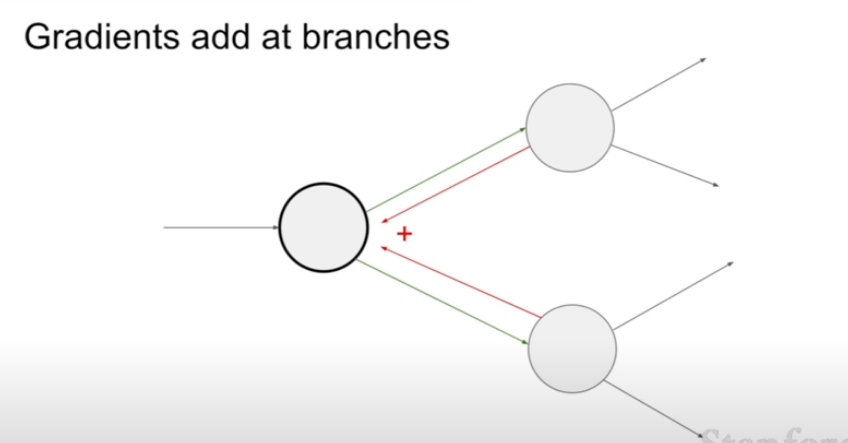
: 여러 노드와 연결되어있는 하나의 노드에서 upstream gradient값을 취하고 합함으로 다변수 chain rule에 대해서 알 수 있고 조금 변경을 시킨다면
forward pass를 할 때 노드들에게 영향을 미칩니다.
: backpropagation일 때, 두 개의 gradient가 하나의 노드에 영향을 미침
벡터의 경우
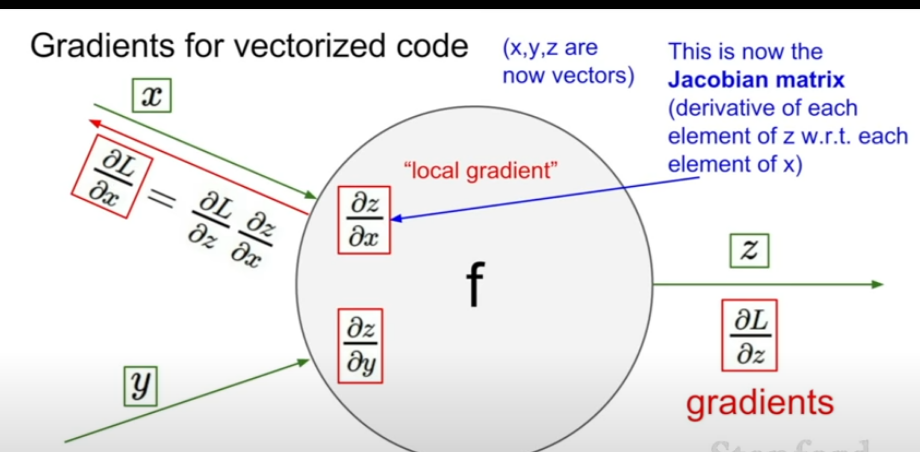
:흐름은 스칼라와 차이가 없지만 gradient가 Jacobian행렬이 된다
이로 인해 각 원소는 각 요소의 미분을 포함하는 행렬이 된다.
- 예시(Vectorized operations)
:CNN에서 볼 수 있고 이 노드는 각 요소별 최대값을 취함(x)
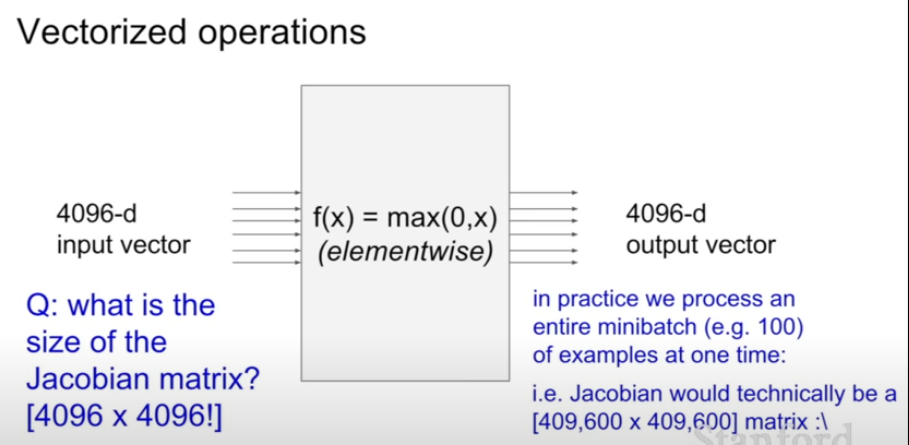
-Jacobian행렬 생성이유
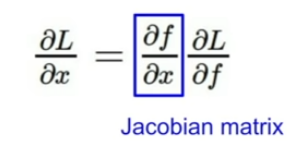
:요소별 최댓값을 갖게 되어서 일어나느 일을 생각하여 편미분한다.
그로 인해 입력의 각 요소, 첫번 째 차원은 출력의 해당 요소에만 영향을 주는 대각행렬을 나타낸다.
:즉, 출력에 대한 x의 영향을 알아보기 위해 쓴다.
+)예시
목표: q의 각각의 요소가 f의 최종값에 어떤 영향을 끼치나(by gradient의 요소를 정량화한다.)

+)예시 2

-backward pass: gradient계산
-forward : 노드의 출력을 계산하는 함수
Neural Networks
신경망: 함수들의 집합으로 비선형의 복잡한 함수를 만들기 위해서
간단한 함수들을 계층적으로 여러 개를 쌓았습니다.
W2는 가중치들의 합이지 최댓값은 아니다

