주성분 분석(PCA)

들어가기

PCA를 이해하기 위해 필요한 개념을 먼저 톺아보도록 합니다

*주성분
여기서 주성분이라 함은 데이터들의 분산(데이터가 흩어진 정도)이 가장 큰 방향벡터입니다.

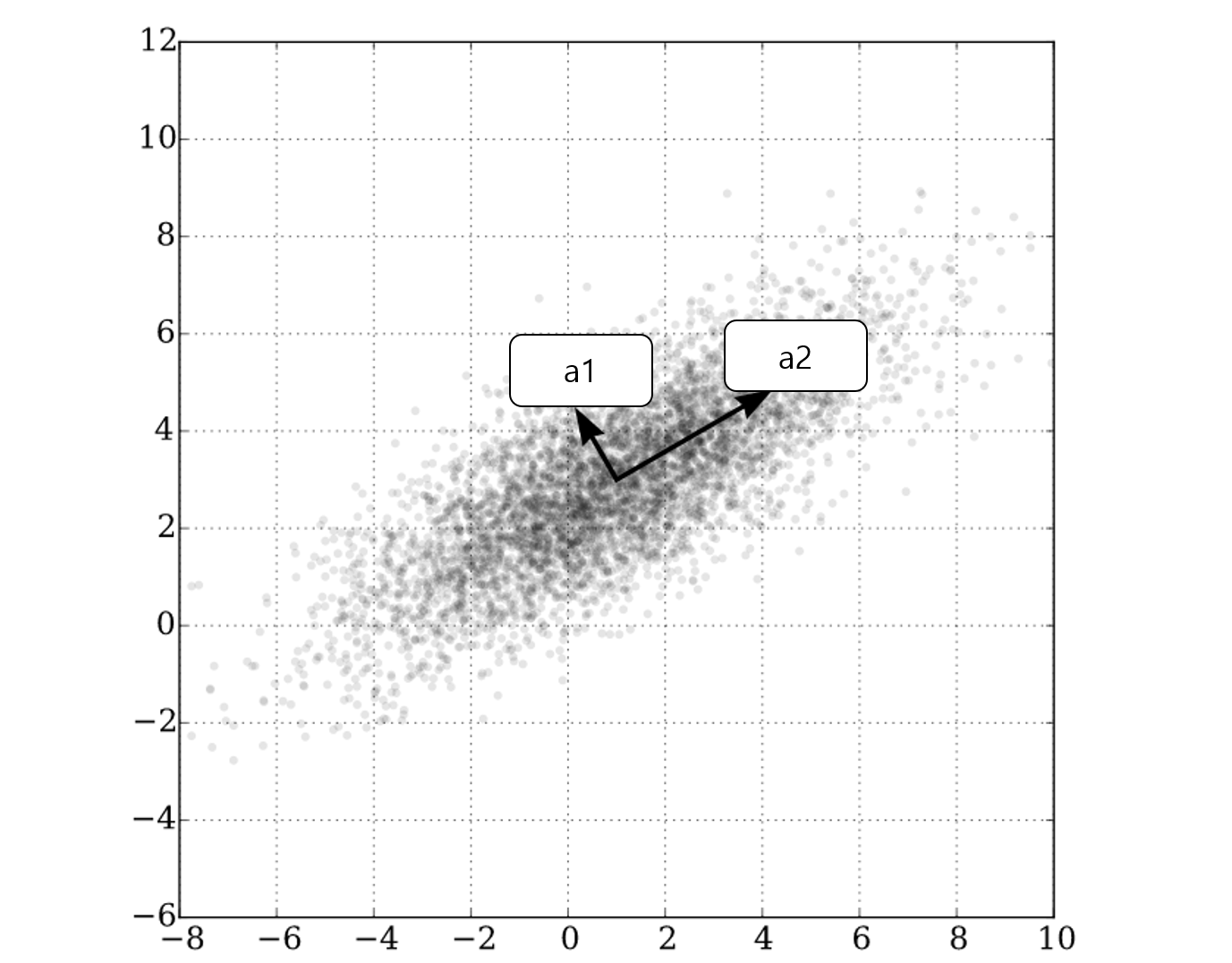
위의 그림에서 주성분은 무엇일까요?

a1과 a2 중에 어느 것이 더 데이터들이 흩어져 있나요? a2

그러므로 주성분은 a2입니다. (대강 감을 잡으셨길 바랍니다)

*공분산 행렬

• 공분산(Covariance): 둘 이상의 값이 연관성을 가지며 분포하는 모양을 전체적으로 나타낸 분산입니다.

• 상관관계(correlation): 공분산 값이 항상 일정하지 않기에, 표준화 하기 위해 공분산에 표준편차로 나눠주면 값이 [-1, 1] 사이에 놓이게 되는 것을 말합니다.

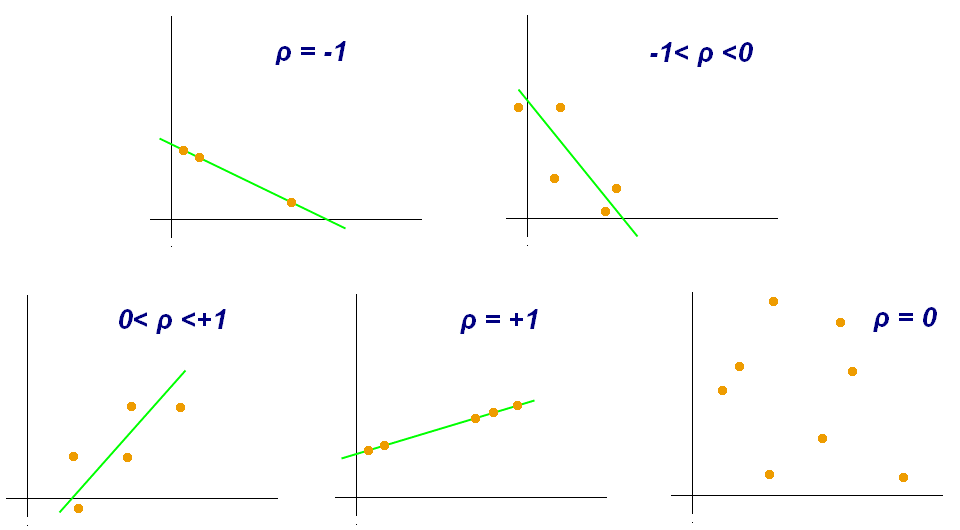
• 공분산 행렬(Covariance matrix)

*정의

X_1의 분산( Var[X_1] )은 x들이 평균을 중심으로 얼마나 흩어져 있는지를 나타내고,
X_1와 X_2의 공분산( Cov[X_1, X_2] )은 X_1, X_2 의 흩어진 정도가 얼마나 서로 상관관계를 가지고 흩어졌는지를 나타냅니다.

*특징

• 각 feature들의 퍼져있는지에 관한 유사도

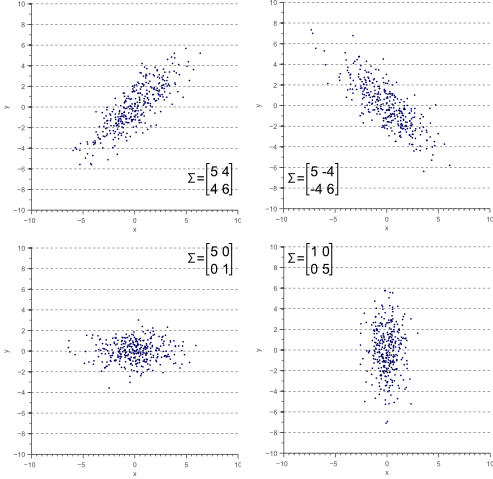
이미지 출처: 링크텍스트

• 데이터를 어떻게 linear transform.

이미지 출처: 링크텍스트

---

PCA

*정의

PCA는 분포된 데이터들의 주성분(Principal Component)를 찾아주는 방법으로 데이터 하나씩에 대한 성분 분석이 아니라, 여러 데이터들이 모여 하나의 분포를 이룰 때 이 분포의 주 성분을 분석해 주는 방법이다.

*벡터 반환

PCA는 n차원 데이터 집합에서 PCA수행 시 n개의 서로 수직인 주성분 벡터를 반환합니다.

*활용

영상인식, 통계 데이터 분석(주성분 찾기), 데이터 압축(차원감소), 노이즈 제거 기타 등등