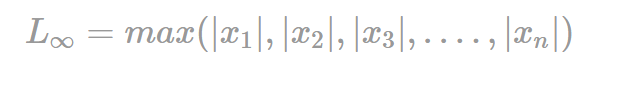L1-L2 Norm

Norm

• 정의: 벡터의 길이 혹은 크기를 측정하는 함수로 측정한 벡터의 크기는 원점~벡터 좌표의 거리, 구성요소의 크기(magnitude)표현

• 조건

  • Absolutely homogeneous
  • Triangle inequality
  • Positive definite

• 특징: 각 요소별로 요소의 절댒값의 p번 곱한 후의 값의 합에 전체 p제곱근한 값

• 수식

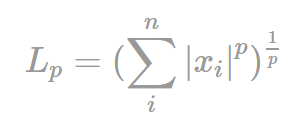
• p는 노름의 차수를 의미합니다.

• n은 대상 벡터의 요소 수

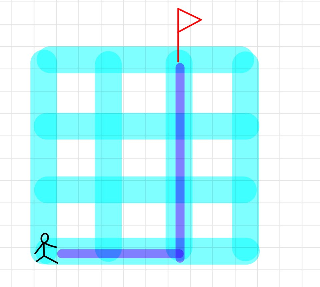
L1 Norm(맨허튼 노름)

• 정의: p가 1인 노름이다.

• 수식

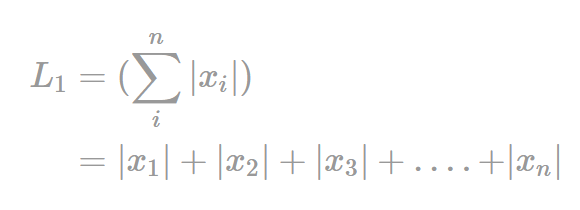
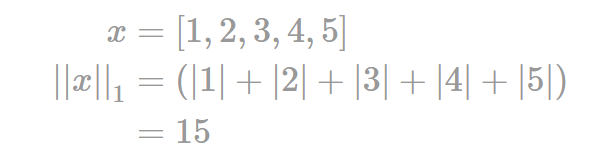
• 특징:

  • 벡터의 요소의 절댓값의 합이기에 요소의 값 변화 파악이 정확하게 가능합니다.

  • Lasso 회귀에서 loss값을 규제할 때 이용

  • 이상치의 영향을 받지 않는다.

• 영역: L1 Regularization, Computer Vision

• Code

import numpy as np
u = np.array([3, -4])
print(np.abs(u).sum()) 

• 사진으로 이해하기

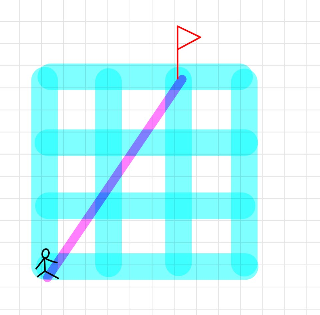
L2 Norm(유큘리드 노름)

• 정의: p가 2인 노름이다.

• 수식

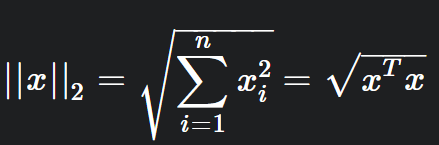
• 특징:

  • n차원 좌표평면에서 벡터의 크기 계산, 피타고라스 정리에서 최단거리 계산할 때 이용

  • 라플라스 근사와 Ridge 회귀 방법에 주로 사용이된다.

  • 이상치에 민감한 방식이다.

• 영역: L2 Regularization, KNN, K-Mean

• Code:

import numpy as np
u = np.array([3,-4])
print(np.linalg.norm(u)) #5.0

• 사진으로 이해하기

Maxium Norm

• p값을 무한대로 보냈을 때의 노름으로 벡터 성분의 최대값을 구합니다.