다중회귀모형
다중회귀모형은 두 개 이상의 독립변수로 종속변수 Y를 설명하고자 하는 모형입니다.
-
k개의 독립변수가 있는 경우(인덱스 i는 관측번호)
- 독립변수 X1, X2, 그리고 Xk 까지를 이용해서 Y를 설명
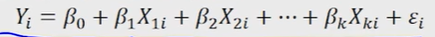
- 입실론(epsilon)_ i는 단순회귀모형과 동일하게 오차항을 나타내며 평균 0, 그리고 분산 시그마(sigma)제곱을 갖는 서로 독립인 정규분포로 가정
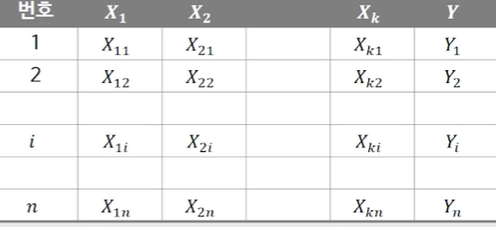
우리가 관측번호 1부터 n까지에 대해서 독립변수 X1에 대해서 관측치가 있고, X2에 대해서 관측치가 있고, 이와 같이 k번째 독립변수 X_k에 대한 관측치가 있고, 그 다음에 종속변수인 Y에 대한 관측치가 있는 이런 데이터 상에서 모형화하고자 하는 것입니다.
-
추정 필요 파라미터(parameter)
- 절편이 하나
- 기울기는 독립변수가 여러 개 있기 때문에 기울기 또한 여러 개가 있겠습니다.
- 오차항의 분산
모형의 추정
회귀계수의 추정
-
최소자승법(least squares method)을 사용
-
다음의 목적함수를 최소화시키는 모형의 기울기들과 절편을 추정
- 목적함수:종속변수의 관측된 값과 모형에 의한 예측된 값(직선식 상의 값) 사이의 오차의 제곱합

- 목적식 최소화 방안
여기도 목적함수 Q를 이와 같이 오차의 제곱합으로 표현하고, 이 Q를 우리가 베타(beta)0, 베타(beta)1, …, 베타(beta)k로 각각 편미분한 것을 0으로 놓고, 전체가 절편을 포함해 총 k+1개의 미지수가 생기는데 이를 k+1개의 연립방정식으로 풀어야합니다.
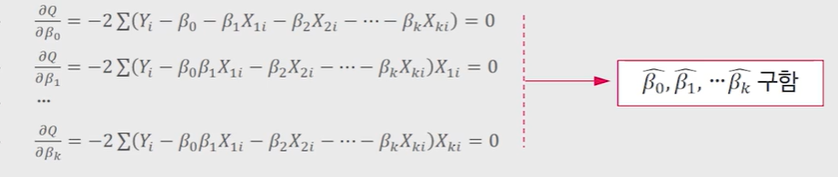
오차항의 분산의 추정
-
오차항은 관측될 수 없으므로 잔차의 표본 분산으로 추정
-
잔차: Y의 실제값과 모형 추정치와의 차
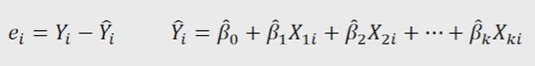
-
잔차(오차)제곱합(residual/error sum of squraes;SSE)
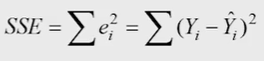
-
분산을 잔차의 표본 분산으로 추정
-
잔차 표본분산은 잔차제곱합을 자유도로 나눈 값
-
이를 잔차평균제곱(mean squared error:MSE)
-
여기서 자유도는 n-k-1
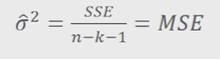
예시
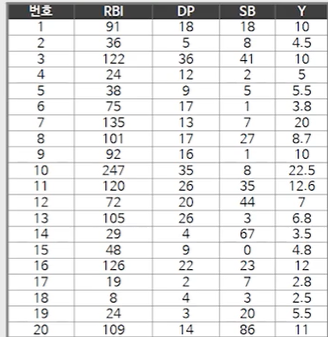
여기서는 야구선수 연봉에 영향을 미치는 요인을 파악하고자 단순히 몇 가지 데이터를 수집한 예입니다.
타점 RBI, 병살 DP, 도루 SB 이런 것에 대해 20명의 선수에 대해 RBI, DP, SB를 조사하고 각 선수의 연봉을 조사했습니다.
그러면 이에 대한 다중회귀모형은 이런 식으로 쓸 수 있게 되겠습니다.
여기서 회귀계수를 추정한 절편은 2.2484로 계산이 되고, RBI에 대한 기울기는, 즉 베타(beta)1_hat은 0.1196, 베타(beta)2는 이렇게 베타(beta)3는 이렇게 되어 결국 추정식은 이렇게 나오는 것을 알 수 있습니다.
그리고 오차분산은 4.06으로 추정되고 있습니다.
이 추정식이 의미하는 바를 살펴보면, RBI에 대한 기울기는 플러스(+)이고, 나머지 DP와 SB는 마이너스(-)입니다.
그래서 플러스(+)라고 하는 것은 연봉을 올리는 요인이 된다고 볼 수 있고 마이너스(-) 계수는 연봉을 내리는 요인이 된다고 볼 수 있겠습니다.
즉, RBI가 1점 증가하면 연봉이 약 0.12 증가한다.
만약 단위가 천만원이라고 하면, “120만원이 증가한다”라고 볼 수 있고, 그 때 우리가 조심해야 할 것은 DP와 SB는 그대로 있고, RBI만 증가하면 그렇게 된다는 것이죠.
그리고 DP는 한점 DP가 더 많아지면, 즉 병살이 한점 많아지면 “연봉이 0.224 감소한다” 이렇게 해석할 수 있겠습니다.
