회귀모형의 진단
모형의 가정
-
오차항 입실론i는 정규분포를 따른다
-
평균은 0:E[입실론i] = 0
-
분산은 관측번호와 관계없이 시그마제곱으로 일정(등분사성): Var[입실론i] = 시그마 제곱
-
오차항은 서로 독립:Cov[입실론i, 입실론j] =0, i /=j
-
모형의 진단
-
잔차 또는 표준 잔차(studentized residual)을 산출하여 가정이 부합하는지 점검
-
주로 잔차 그래프를 통한 시각적 진단
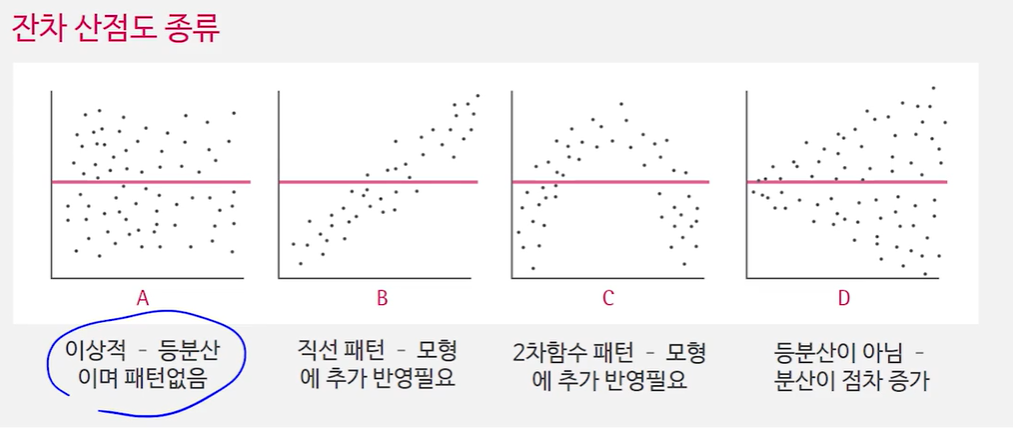
- Y추정치 VS 잔차 산점도: 산포가 일정한지, 어떤 패턴이 없는지 점검
- 잔차에 대한 정규확률분포도: 잔차를 순서로 나열하고 순위에 대항하는 누적확률을 추정하여 그래프로 나태낸 후 직선식에 가깝게 찍히면 정규 분포를 따른다고 할 수 있음
예제 BMI와 GMP관계
-
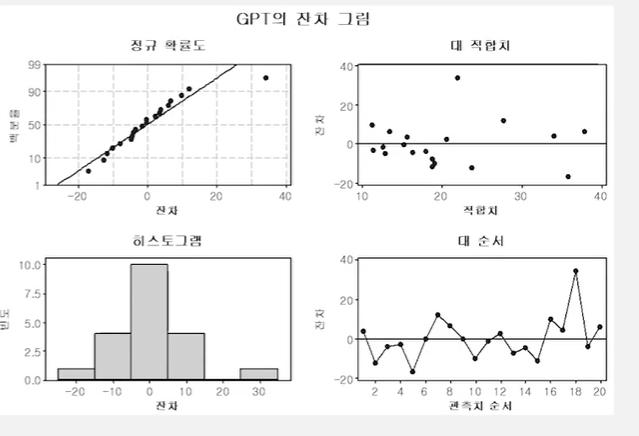
모형을 추정한 후 잔차 그래프 그린 것.
-
모형을 진단하기에는 관측수가 20으로 비교적 작다
-
잔차의 정규확률도 및 히스토그램을 볼 때 정규분포를 크게 벗어나지 않음
-
잔차들이 등부산성을 벗어나거나 특정 패턴을 나타내진 않음
반응치의 예측
Y의 추정식을 바탕으로 새로운 X값에 대한 Y값 평균치(평균 반응치) 추정
- 추정식

- 새로운 X값 x0에서 Y값 평균치 추정
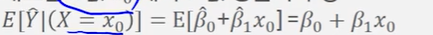
- X= x0에서의 평균 반응치 추정값
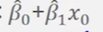
평균 반응치의 신뢰구간
-
평균 반응치 추정값과 미래반응치 예측값은 동일
-
평균방응치 신뢰구간과 미래 반응치 예측 구간은 다름
-
예측 구간은 새로운 측정오차가 추가되어 신뢰구간보다 넓다
-
새로운 X값에서 반응치를 반복측정하는 경우에는 신뢰구간을, 한번만 측정하는 경우 예측 구간을 사용함
-
평균 반응치 추정값의 분산
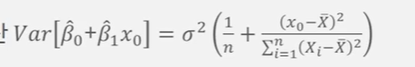
- 100(1-알파)% 신뢰구간
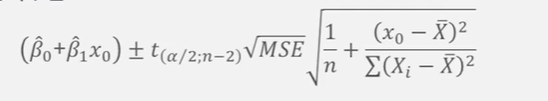
예제 BMI 와 GPT 관계
-
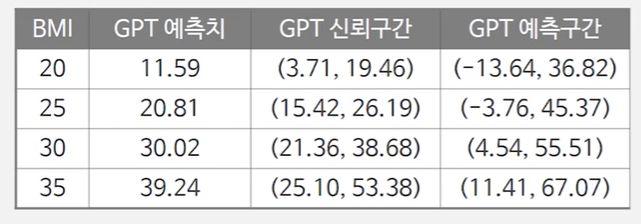
추정식:GPT = -25.28 + 1.8435 BMI
-
BMI가 20,25,30,35일 때 GPT를 예측하면 예측치, 평균 반응치 95% 신뢰구간, 미래반응치 95% 예측구간
-
BMI = 30, GPT의 신뢰구간을 알려고한다면(21.36, 38.68)
-
BMI = 30, 어느 특정인의 GPT 예측구간을 알고자 하면(4.54, 55.51)
