목차

1. 신경망

2. 활성함수와 손실함수

3. 경사하강법

4. 오차역전파법

5. Step by Step

6. 추론과정 구현 및 정확도 계산

7. 전체 학습

신경망

-인공신경망: 생물학적 뉴런의 네트워크에서 영감받은 머신러닝 모델로 딥러닝의 핵심이다 그 이유는 강력하고 확정이 좋기 때문이다.

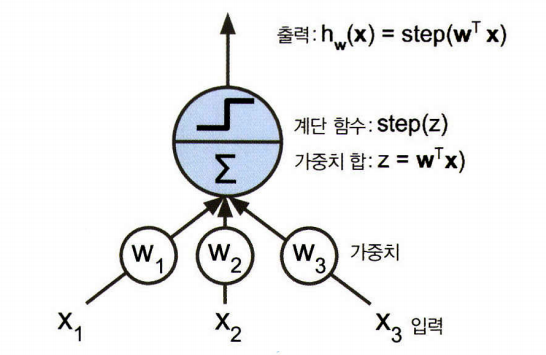
-퍼셉트론: 인간의 뇌 속의 신경망 구조에서 착안된 것으로 가장 간단한 인공 신경망 중 하나이다. 그리고 입출력이 어떤 숫자이고 각각의 가중치와연관

-인공 뉴런

+)TLU :간단한 선형 이진 분류 문제에 사용 가능.
입력의 조합이 임곗값을 넘으면 양성 클래스 출력,그렇지 않으면 음성 클래스

최적의 가중치를 찾는다.

+) LTU

-계단함수(Step function)

:TLU는 입력의 가중치 합을 계산한 뒤 계단함수를 통해 결과 출력

:step(z)

:출력을 0,1로 이진값만 반환하고 나머지는 무시한다.

-다중 퍼셉트론(MLP)

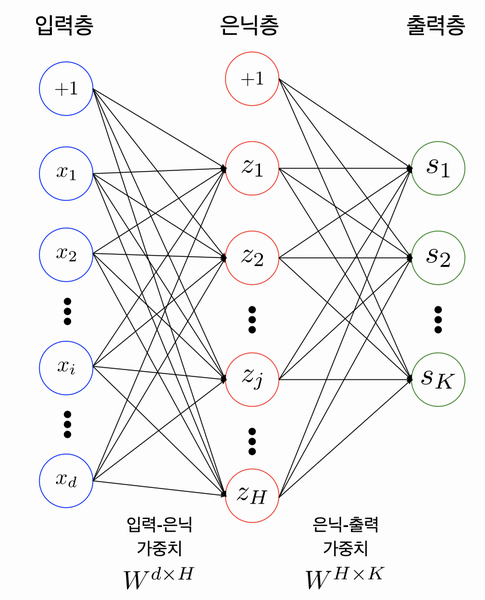
-구성
+) +1: bias term : 입력값 출력값 모두 0이 되는 경우를 방지.

+)입력층: 입력 뉴런 + 편향뉴런(항상 1을 출력)으로 구성. 행단위

+)은닉층: 편향 뉴런 있음, 랜덤하게 가중치 초기화.

+)출력층: 출력 뉴런있음

+)인공 뉴런층 계산(완전 연결층일 경우)

+)FNN: 신호가 입->출로 한 방양만으로 흐른다

+)DNN:은닉층을 여러 개 쌓아 올린 인공 신경망

-케라스API:인공 신경망을 간결하고 다양하게 구현하게 해주는 API.

-MNIST :숫자 이미지 데이터셋으로 학습용으로 많이 사용있다.

• 데이터 셋의 딕셔너리 구조
  

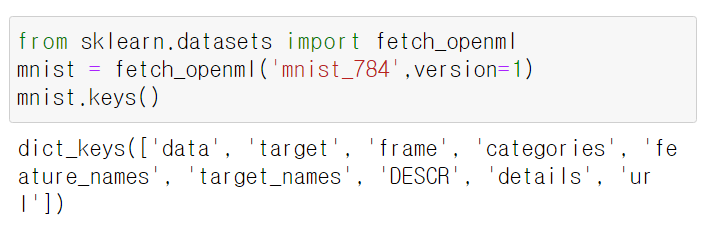
  +)데이터셋을 설명하는 DESCR키
  +)data키: 샘플-행 / 특성- 열 로 구성된 배열
  +)레이블 배열을 담은 target키
  

• 숫자 나타내기

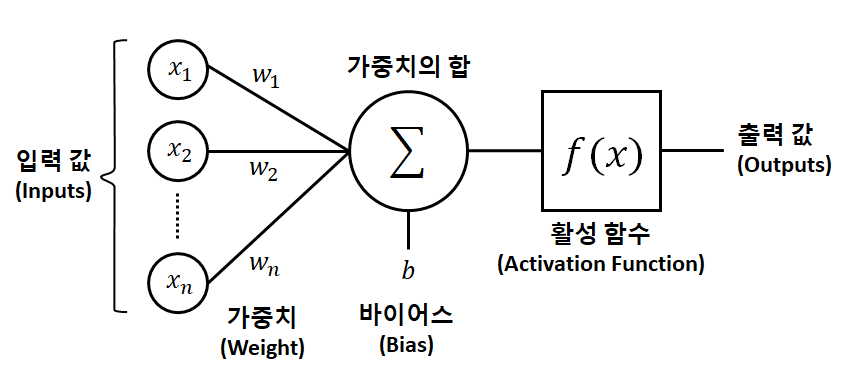
-Parameter/Weights

:입~은 / 은~출 사이에 있는 것으로 인접한 레이어 관계를 나타냄

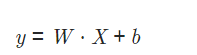
활성화 함수와 손실함수

활성화함수(Activation Functions0

0.정의 및 특성

-비선형 함수를 이용함으로 표현력이 좋아진다.

-이전 레이어에 대한 가중 합의 크기에 따라 활성 여부가 달라짐

-목적에 따라 레이어의 역할에 따라 선택적 적용.

-비선형 추가를 통해서 복잡한 문제를 풀기 위함이다

1.Sigmoid(로지스틱)함수

• 특징

  :계단함수의 발전형(수평선 함수라 gradient가 없다.)

  :0~1사이의 함수이고 0~1사이값 반환

  :연속형 데이터

  :이상치가 들어와도 0 or 1로 수렴하므로 이상치가 들어와도 상관없음

• 장점

:출력값의 범위가 작기 때문에 경사 하강법 시행 시, 기울기가 급격하게 변하는 기울기 폭주(Gradient Exploding)가 발생하지 않는다

:0과 1에 가까운 값을 통해 이진 분류

• 단점

  :exp함수(e함수) 사용 시 비용이 크다

  :출력 값의 범위가 너무 좁아서 경사하강법 수행시 0에 수렴하는 기울기 손실(gradient vanishing)이 발생한다.

  --> 출력의 가중치 합이 입력의 가중치 합보다 크게 되어 편향이동 발생.
  이로 인해 gradient = 0. 역전파 진행시 Layer에 신호 전달 안됨

  :학습 속도 저하

-> 출력값이 모두 양수이기 때문에 기울기가 무조건 양수 or 음수이다..
-> 기울기 업데이트가 일정하지 않아 학습 효율성이 떨어진다.

:시그모이드 함수 예시

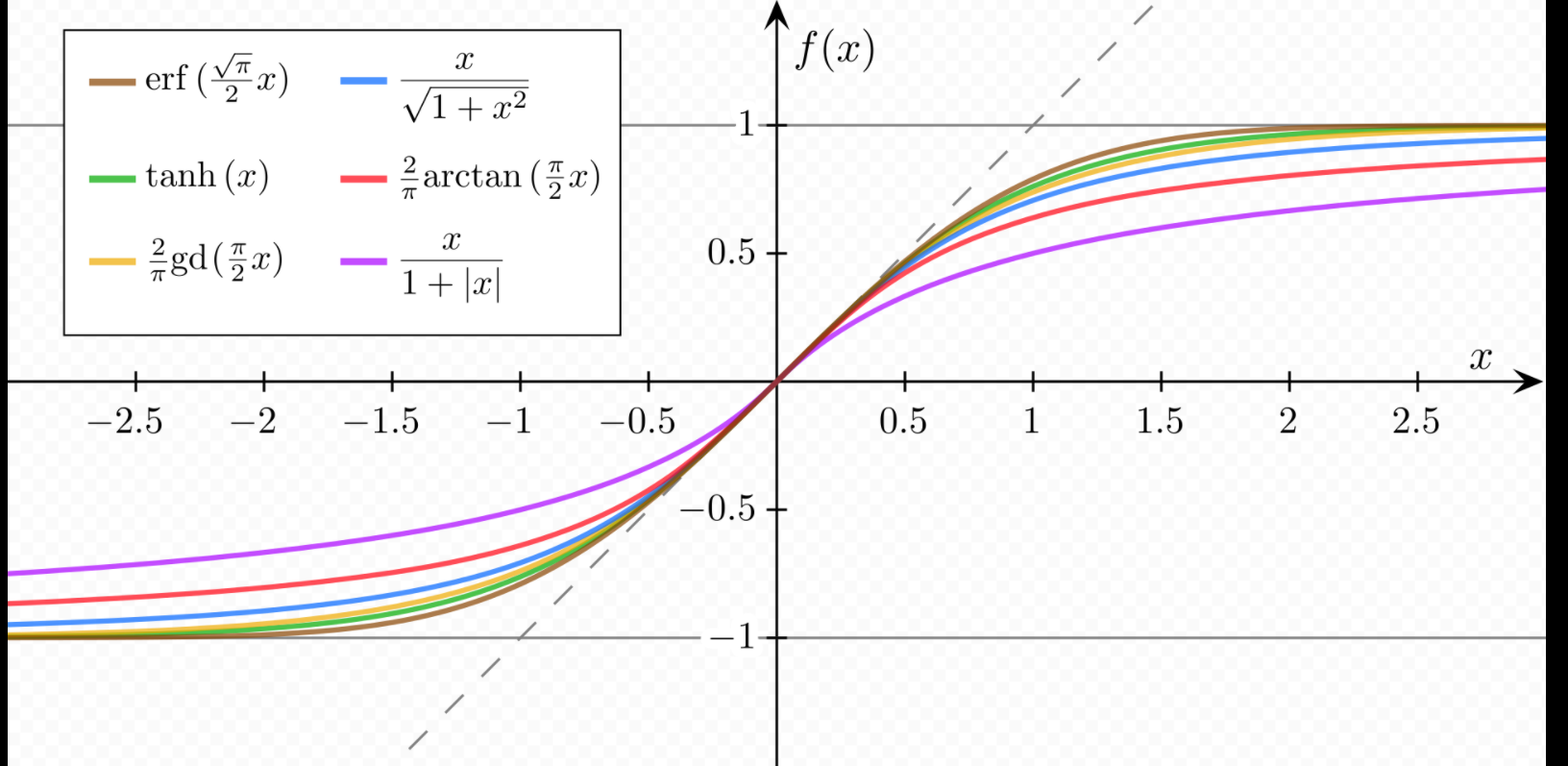
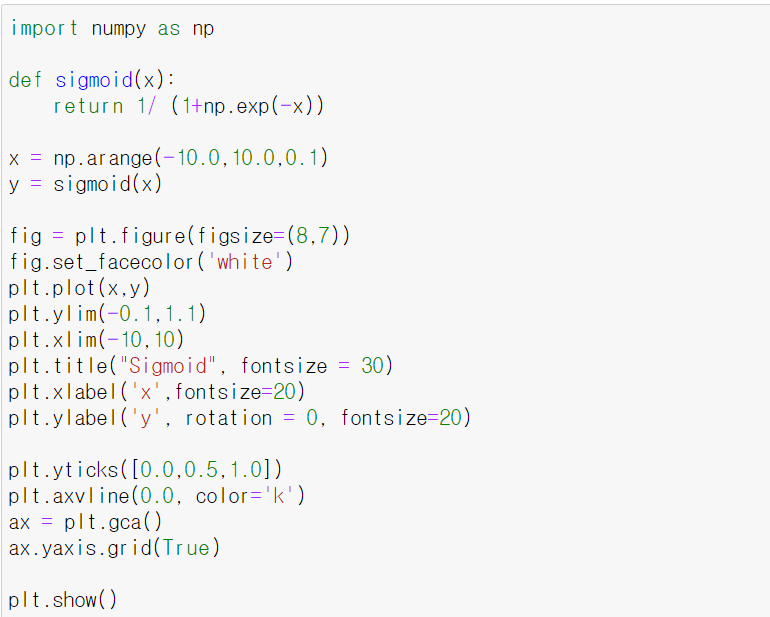
:시그모이드 함수를 코드로 구현

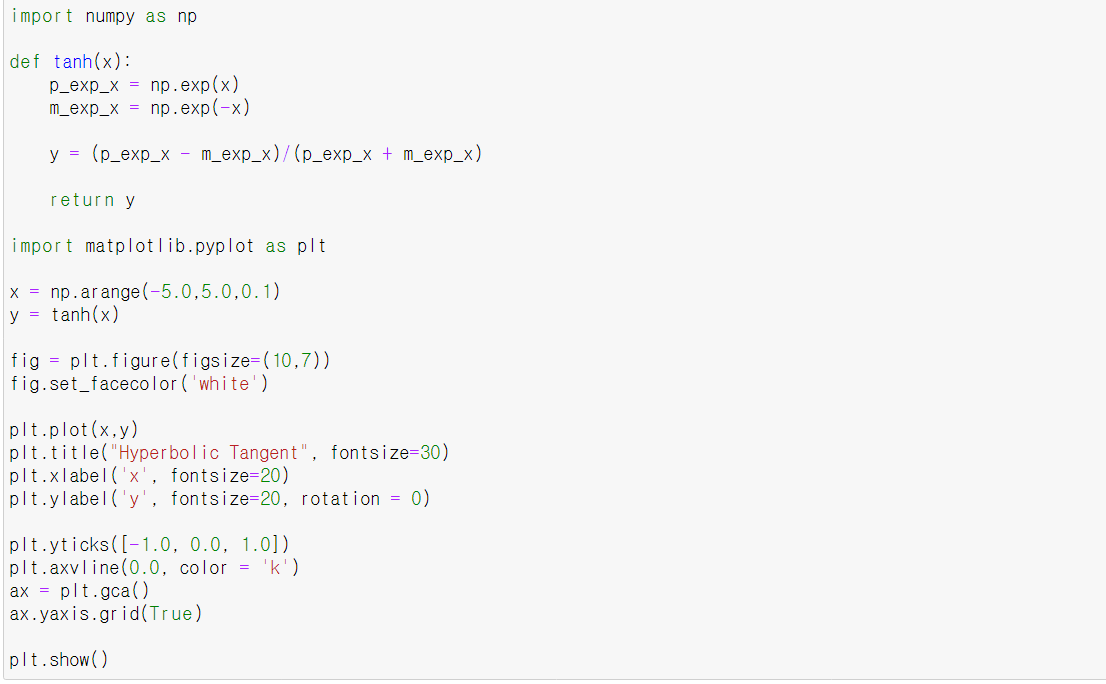
2.Tanh(하이퍼볼릭 탄젠트 함수 [쌍곡 탄젠트 함수])

0.정의 및 특징

:쌍곡선 함수로, 표준 쌍곡선을 매개변수로 한다.

:S자 모양이고 미분이 가능하다

:출력 범위는 -1 ~ 1 사이이다. -> 기울기 양수 음수 가능, 범위가 넓어서
기울기 손실 증상이 적은 편.

:중앙값 - 0 --> 편향이동 발생하지 않음

: 훈련 초기에 각 층의 출력을 원점 근처로 모아 수렴 빠르게 함

:은닉층에서 시그모이드 함수 같은 레이러를 쌓을 때 좋음

• 코드로 하이퍼볼릭 탄젠트 구현

  

3.ReLU함수

:함수는 연속적이지만 z = 0에서 미분 불가!

:z < 0일 경우 도함수는 0이다.

:실제로 잘 작동하고 계산 속도가 빠르다.

:출력에 최댓값이 없어 경사 하강법에 일부 문제 완환.

:은닉층에서 다층 신경망을 쌓음.

: +신호는 그대로 / -신호는 차단하는 함수

: 양수면 자기 자신 반환 / 음수면 0 반환

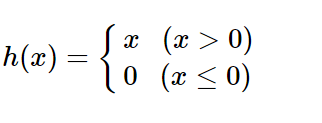
• 장점

  :기울기 손실이 발생하지 않음

  -> 출력값의 범위가 넓고 양수일 때 음수 일 때 특성이 각각 있어서 특정 값에 수렴하지 않기 때문이다.

  :속도가 매우 빠름

• 단점

  :음수 값이 들어오는 경우 모두 0으로 반환

  : 기울기가 0이 되어 가중치 업데이트 안됨

  :죽은 뉴런 상태.

  :은닉층에서만 쓰임

  : 출력값이 0 또는 양수이므로 시그모이드처럼 지그재그 현상 발생.

  :0에서 미분이 불가능

• 코드로 함수 짜기

  

  손실함수(Loss Functions)

  :우리가 원하는 정답과 전달된 신호 정보들 사이의 차이를 계산하고 줄이기 위해 파라미터를 조절하는 함수라고 한다.

  -종류

  +)평균제곱오차(MSE:Mean Square Error)

  

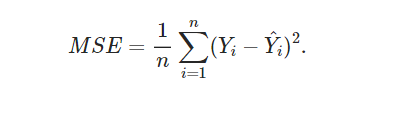
  • 코드로 구현

    

    +)교차 엔트로피( Cross Entropy)

  • 코드로 구현
    

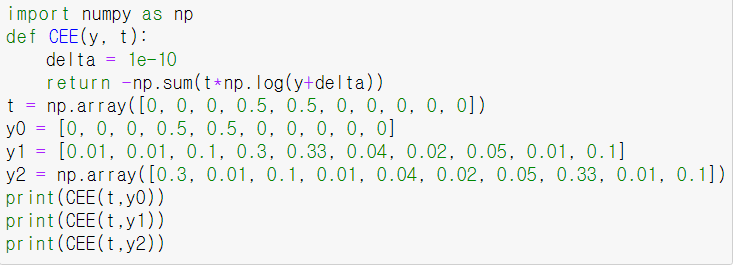
    : 두 확률 분포 사이의 유사도가 클수록 작아짐
    

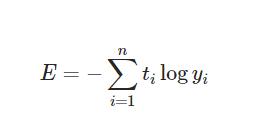
경사하강법(GD:gradient descent)

0.정의 및 특징

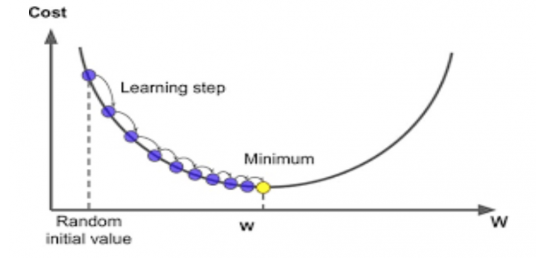
: 최적의 해법을 찾을 수 있는 최적화 알고리즘

: 손실함수를 최소화 하기 위해서 여러번 파라미터 조정함.

:gradient가 감소하는 방향으로 진행하다가 0이되면 최솟값

:파라미터 벡터를 임의값으로 한 후 무작위 초기화를 통해 손실함수가 감소되는 방향으로 진행하여 최솟값에 수렴할 때까지 점진적으로 향상시킨다.

: 최솟값으로 갈 수록 스텝의 크기가 줄어든다

1.학습률(learning rate)

:하이퍼파라미터인 학습률로 스텝의 크기 조절.

: 학습 시간과 관련이 있음

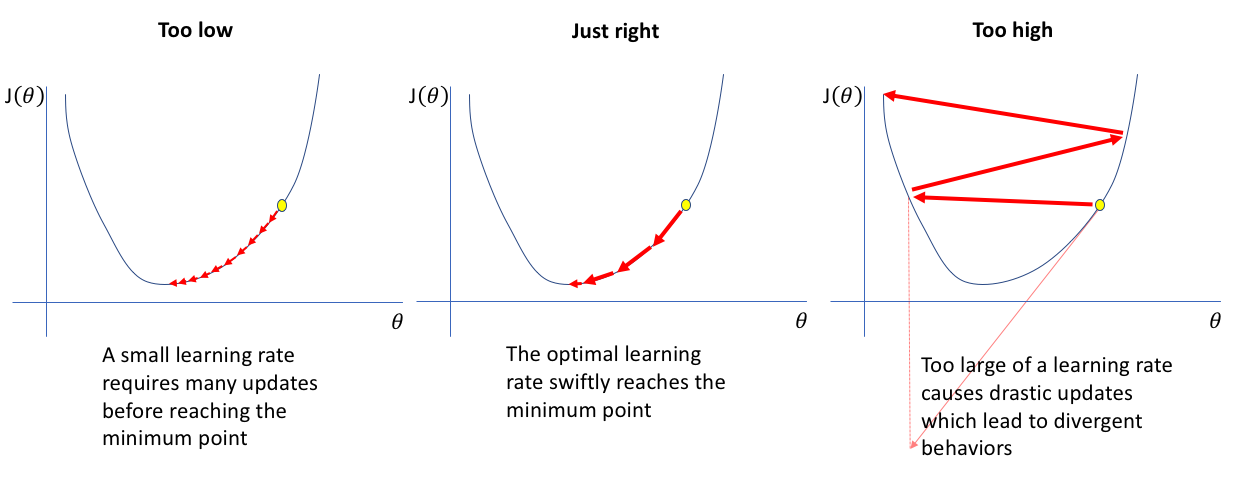
:학습률이 너무 작으면 시간이 오래 걸리고

:학습률이 너무 크면 발산하여 위로 올라간다.

2.가중치 초기화(Weight Initialization)

• 초기 가중치 설정

  1)초기값을 모두 0으로 설정한 경우

  뉴런들이 같은 값을 같고 역전파 과정에서 update가 동일하게 이뤄짐

  2)활성화 함수로 sigmoid사용 시 정규 분포 사용

  : 미분값이 소실되는 문제를 막는다

3)2의 case에서 표준편차 줄였을 때

:중간값 0.5에 몰린다

• 가중치 초기화

  : 더 나은 학습을 하기 위함이다

1. LeCun Initialization

   :역전파를 위해 수행한다.

• 정규분포

  

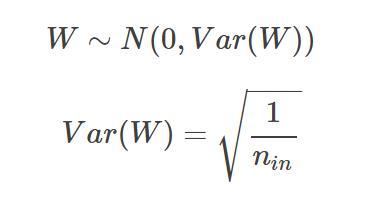
• 균등분포

  

2. Xavier Initialization
   :이전 노드와 다음 노드의 개수에 의존한다.

• Normal

  

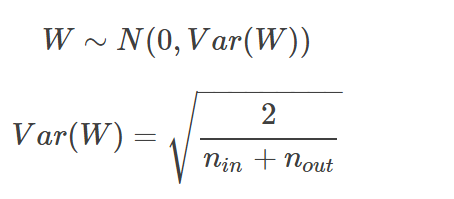
• Uniform

  

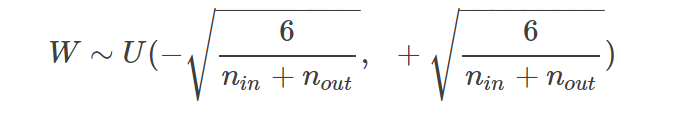
3. He Initialization

   :초기값 설정이 너무 비효율적인 결과를 보였을 때 사용한다.

• Normal

  

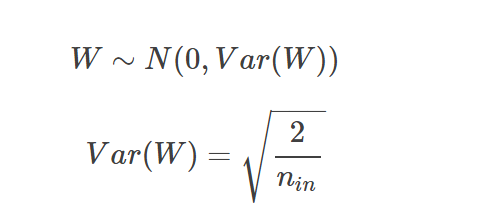
• Uniform

  

  오차역전파(Backpropagation)

  0.정의

  :네트워크를 정방향 한 번, 역방향 한 번씩 통과만으로도 모든 모델 파라미터에 네트워크 오차의 gradient를 계산한다

  :출력층의 결과와 내가 뽑고자 하는 target값의 차이를 구한 후 오차값을 각 레이어들을 지나며 역전파를 한 후 노드를 가지고 변수 갱신.

  :오차를 감소시키기 위해서 각 연결 가중치와 편향값이 어떻게 바뀌어야 하는지 알게된다

  :기울기를 입력층까지 전달하며 파라미터 조정한다.

  :MLP를 학습시키기 위한 일반적인 알고리즘으로 SGD에서 자주 쓰임