벡터공간II

부분공간

*벡터 공간

같은 수의 성분을 가진 벡터가 두 개 이상 있을 때, 이 벡터들이 만드는 공간을 의미합니다.

*부분 공간

두 개 이상의 벡터로 인해 만들어진 공간에 속해있는 것들을 말합니다.

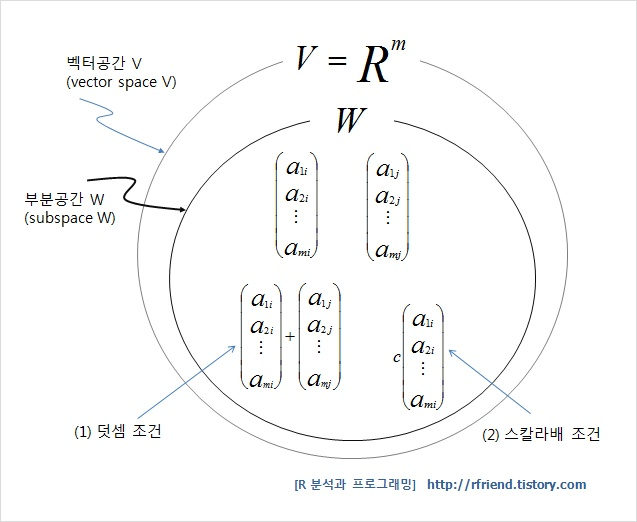
*특징

1. 벡터의 덧셈 법칙 성립

2. 스칼라 곱셈 법칙 성립

3. 영벡터 포함

*생성공간(span)

벡터공간 V의 공집합이 아닌 부분집합 S가 있을 때, S의 생성공간읜 S의 벡터를 사용하고, 이렇게 만들어진 일차결합의 집합을 의미합니다.

---

일차결합과 연립일차 방정식

*일차 결합

n차원 벡터들의 집합이 존재한, 아래의 이미지와 같이 집합 S의 벡터들의 일차결합이라 한다. .벡터v는 v1₁, v2, v3의 일차결합이다.

*연립방정식

• 방식

  • 두 방정식의 위치 바꾸기
  • 방정식에 0이 아닌 상수 곱하기
  • 상수배하여 얻은 방정식을 다른 방정식에 더하기

• 성질

  • 각 방정식에 처음 등장하는 0이 아닌 계수는 1이다.
  • 다른 행에서 미지수에 붙은 계수는 0이다.
  • 처음 등장하는 미주의 첨자는 다음 행으로 내려갈 때마다 반드시 증가