벡터공간(Vector Spaces)

개론

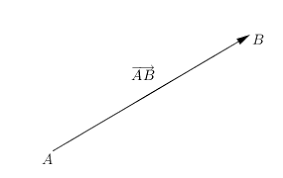
• 벡터: 크기와 방향을 모두 가진 물리량으로 보통 화살표로 표현합니다.

• 벡터의 크기: 화살표의 길이

• 벡터의 방향: 화살표의 방향

• 크기와 방향이 같다면 같은 벡터입니다.

• 합: 두 물리량이 결합될 때 나타나는 효과는 두 벡터를 결합시켜 얻은 합성벡터입니다.

• 평생사변형 법칙: 두 벡터를 결합시키는 규칙

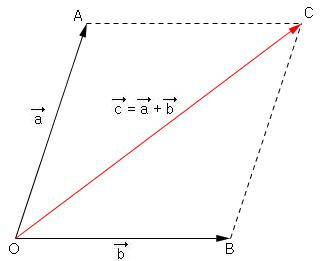
시점이 O로 일치하는 두 벡터 a,b의 합은 점 O에서 시작하는 벡터이고, a와b를 이웃한 변으로 하는 평행사변형의 대각선으로 나타나게 됩니다.

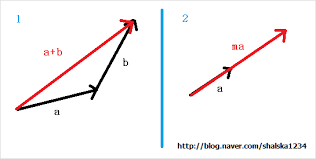
벡터의 합과 벡터의 스칼라 곱

• 벡터의 스칼라 곱은 벡터의 크기에 실수를 곱하면 확대하거나 축소가 가능합니다.
• 벡터의 평행: 두 벡터의 방향이 같거나 180도 반대인 벡터들을 말합니다.

• 벡터의 대수적 성질

*훗날, 직선의 방정식과 평면의 방정식을 나타내는 데 사용이 됩니다.

*벡터공간 혹은 선형공간에서 일어납니다.

• 모든 벡터 x,y에 대하여 x + y = y + x이다(교환법칙 성립)
• 모든 벡터 x,y,z에 대하여 (x+y) +z = x + (y+x)이다. (결합법칙 성립)
• 모든 벡터 x에 대하여 x+ 0 = x를 만족하는 벡터 0이 존재한다.
• 각 벡터 x마다 x+y=0을 만족하는 벡터 y가 존재한다.
• 모든 벡터 x에 대하여 1x=x이다.
• 모든 실수 a,b와 모든 벡터 x에 대하여 (ab)x = a(bx)이다.
• 모든 실수 a와 모든 벡터 x,y에 대하여 a(x+y) = ax +ay이다.
• 모든 실수 a,b와 모든 벡터 x에 대하여 (a+b)x = ax+bx이다.

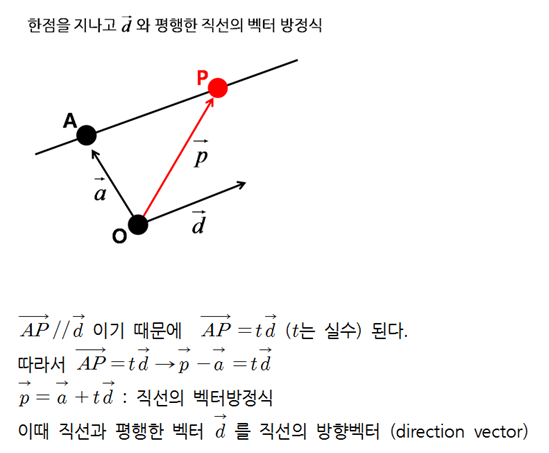
• 직선의 방정식

https://j1w2k3.tistory.com/628

P(x,y) 와 A(x1,y1)라고 할 때, x의 값은 어떻게 구할 수 있을까요?

우리는 벡터의 합과 벡터 스칼라의 곱을 이용하면 구할 수 있습니다.

점 P의 좌표는 점A 보다 크면서 벡터 d가 움직인 거리만큼 더한 것입니다.

고로, x = x1 + td입니다. P(x1+td, y1+td)가 되는 것입니다.

직선의 벡터 방정식은 OP는 어떻게 구할까요? (벡터의 합 이용)

위의 그림처럼, 벡터p는 벡터 a 와 벡터 td의 합입니다. 여기서, 왜 벡터 d에다가 실수 t를 곱한 것일까요?

길이를 맞춰주기 위해서입니다. 지금 그림에선 필요가 없을 수 있지만, 방향벡터 d가 벡터p보다 얼마나 크고 작은지를 모르기 때문입니다.