Intro
회귀분석의 개념에 대해 이해하고, 최소자승법에 의한 회귀계수 추정 및 오차항 분산 추정에 대한 이해를 중점으로 블로그를 작성했습니다.
회귀 분석(Regression Analysis)
*정의
관심있는 하나의 변수를 설명하는데 있어 이에 영향을 주는 다른 변수들간의 통계적 인과관계를 분석
*독립변수(independent variable): 원인의 역할을 하는 변수
*종속변수(dependent variable): 결과를 관측 하는 변수
회귀 모형

단순 회귀 모형

하나의 독립변수로 종속변수를 설명되는 것으로 Y의 변동이 X에 따라서 선형 관계를 갖는 모형을 의미하기에 직선 식을 중심으로 X가 변함에 따라 Y가 어떻게 변하는 지를 직선 모형을 사용하여 설명
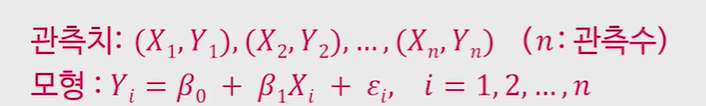
-
X의 값은 주어지므로 확률변수가 아니다
-
추정필요 파라미터
- 베타1: 직선식의 기울기
- 베타제로: 직선식의 절편
- 입실론 제곱: 오차항의 분산
모형의 추정
절편 베타제로와 기울기 베타1의 추정
-
최소자승법(least squares method)사용
-
다음의 목적함수를 최소화 시키는 직선식의 기울기와 절편 추정
-
목적함수란: 종속변수의 관측된 값과 모형에의해 예측된 값(직선식 상의 값) 사이의 오차의 제곱합
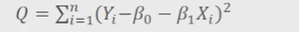
-
-
목적식 최소화 방안
- (X,Y)값은 관측된 값이므로 Q를 베타제로와 베타1의 함수로 간주
- Q를 베타제로와 베타1으로 각각 편미분하여 0으로 놓고 연립방정식으로 풀기
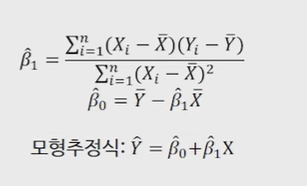
오차항의 분산의 추정
-
오차항은 관측될 수 없으므로, 잔차의 표본 분산으로 추정
- 잔차(residual):Y의 실제값과 모형 추정치와의 차
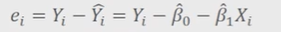
- 잔차(오차)제곱합(residual/error sum of squares:SSE)

-
오차항의 분산을 잔차의 표본 분산으로 추정
- 잔차 표본분산으 잔차제곱합을 자유도(n-2)으로 나눈 값
- 2는 베타제로와 베타1을 뺀 값
- 이를 잔차평균제곱(mean squared error:MSE)
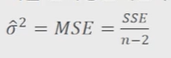
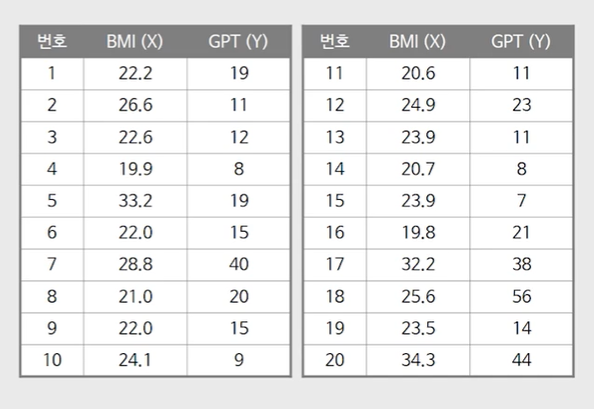
예제: 체질량지수인 BMI가 간기능수치인 GPT에 어떤 영향을 주는지 알아보고자 20명에 대하여 BMI와 GPT측정
*데이터
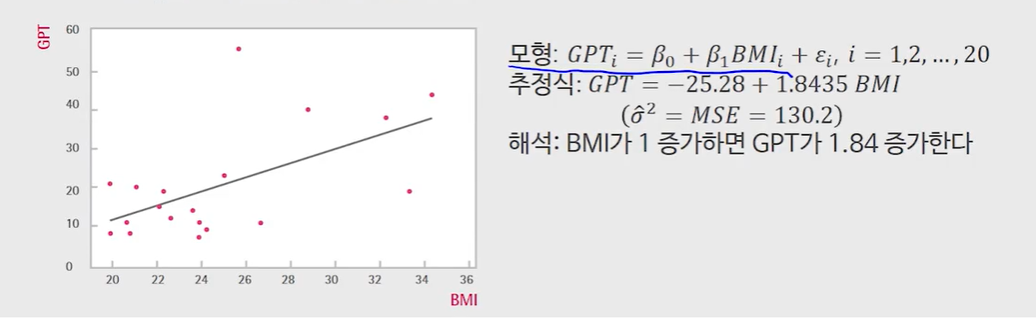
*그래프 해석
다중 회귀 모형: 여러 독립변수로 종속변수 설명
