회계계수 추정량의 분포
회귀계수의 신뢰구간 유도나 검증을 위해서는 추정량의 분포가 필요
-
Y가 관측되기 전에는 확률변수이므로 기울기의 추정량도 확률 변수이다
-
베타1은 정규 분포를 따른다
-
절편 추정량도 유사한 성질을 가진다
-
오차분산 추정량 성질

- 기울기
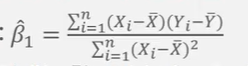
모형의 검정
회귀계수 베타 제로와 베타1에 대한 검정으로 특히 기울기 베타1에 대한 검정이 필요
-
(X,Y)에 대한 관측치가 있으면 회귀계수가 추정이 되지만 통계적 의미를 갖는지는 파익이 필요
-
기울기 베타1이 통계적으로 0이면 X가 Y를 설명할 수 없다.
기울기 베타1에 대한 t-검정
-
H0(귀무가설): 베타1 = 0 vs H1(대립가설):베타1 /= 0
-
검정 통계량
- 분모는 분자의 표준오차(Standard error)

- 판정: p-값이 유의수준 알파보다 작으면 귀무가설이 기각
t-값과 p-값
-
p-값은 t-값이 T일 때 아래의 색깔 부분의 면적에 해당하는 확률
-
p-값은 알파보다 작거나 같을 때 유의수준 알파에서 기무가설이 기각
단순회귀모형에서 회귀계수 추론결과

예제 BMI와 GPT의 관계

-
추정식:GPT = -25.28 + 1.8435 BMI
-
BMI기울기는 1.8435로 추정이되고 t-값이 3.08이고 p-값이 0.006으로유의수준을 1%로 고려하여야 통계적으로 유의하므로 이 뜻은 곳 귀무가설을 기각하기에 BMI가 통계적으로 유의미하게 GPT에 영향을 준다고 할 수 있습니다.
*모형의 적합도와 결정계수(R^2)
-
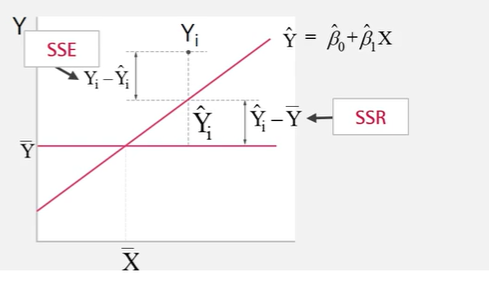
회귀모형은 Y값의 변동을 설명하는데 독립변수 X를 도입하는 것으로 볼 수 있다
-
Y값의 변동은 관측치가 주어지면 어떤 독립변수를 대입하건 일정하게 진행되고 이를 전체제곱합(total sum of squares:SST)라고 합니다.
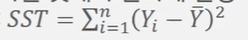
- SST = SSE +SSR
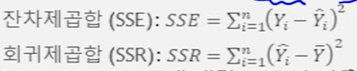
-
R-square:SST에 대한 SSR의 비율
- R^2 = SSR/SST = 1- (SSE/SST)
- 모형이 SST를 얼마나 설명하는지를 나타내는 척도
- O<= R^2 <=1
F-검정
F검정의 아이디어
-
시그마제곱의 두 가지 추정량 고려
- MSE는 항상 시그마제곱의 불편 추정량
- MSR은 귀무가설이 옳을 때 시그마제곱이 불편추정량으로 사용 가능
- 따라서 MSR/MSE비율을 산출하면 귀무가설이 옳을 때 1에 가까운 값
- 그러나 위의 비율이 1보다 매우 큰 값을 가지는 귀무가설이 엃지 않다고 판정
회귀 모형에 대한 유의성 검정
-
다중 회귀모형을 염두에 둔 검정
-
도입된 독립변수들 중 적어도 하나 이상이 Y값을 유의하게 설명하는지를 파악할 필요 있음
-
단순 회귀모형에서는 독립변수가 하나이므로 t-검정으로 동일
F-검정 과정
-
귀무가설: 베타1=0 VS 대립가설: 베타1 /=0
-
검정 통계량(귀무 가설이 옳을 경우)
F0 = (SSR/1)/ (SSE/(n-2)) = MSR/MSE ~ F1,n-2(자유도가 1, n-2인 F-분포)
- 판정:p-값 P{F1,n-2 >=F0}이 유의수준 알파보다 작으면 귀무가설 기각
단순회귀모형의 분산분석(ANONVA)

*예제: BMI와 GPT관계)

-
결정계수 R^2 = SSR/SST = 1235.5 / 3578.9 =34.5%(GPT의 변동을 BMI가 34.5%라고 설명)
-
F-검정에서 유의수준 1%에서도 유의하므로 모형이 의미있다고 판정
