경사하강법.
머신러닝, 딥러닝을 공부하기 시작하면 자주 마주하게 되는 단어다.
글로 정리하기 전 chatgpt에게 물어봤다.
우리말로 요약하자면 경사하강법이란,
- loss function을 최적화하기 위한 알고리즘.
- 손실 함수 기울기 계산 후steepest descent 방향으로 매개변수를 업데이트
- learning rate로 step size 조정
- criterion 만족 시 중단
내가 굳이 해야할 필요가 있나라는 생각이 들 정도로 잘 답변해준다.
그래도 나만의 답으로 정리해본다.
간단하고 이해하기 쉽게.
경사 하강법, 용어를 풀어보면
경사는 함수의 기울기를 뜻하고,
하강법은 말 그대로 하강(떨어짐), 즉 감소를 뜻한다.
정리하면 '함수의 기울기를 감소하는 방법' 이라고 할 수 있겠다.
식으로 표현하면 다음과 같다. (다변수 함수 일 때)
이 때 는 Learning rate(step size)이다.
질문 1. 경사하강법을 왜 사용할까?
-> 모델을 학습시킬 때 우리는 정답값(GT)과 예측값의 차이인
손실 함수(Loss Function)의 크기를 최소화 시키는 Parameter를 찾는 것이 목표이다.
함수 값을 증가시키고 싶다면 미분값을 더하고, 감소시키고 싶으면 미분 값을 빼야한다.
우리는 최소값(극소값)을 찾기를 원하기 때문에
미분값을 빼는 경사하강법을 사용한다.
+) 최대값(극대값) 찾을 때는 경사상승법(Gradient Ascent)
질문 2. 경사하강법의 단점(한계점)은?
-> 대표적으로 두 가지 문제점이 있다.
1. Local Minimum
2. Saddle Point
이미지로 보자면 다음과 같다.
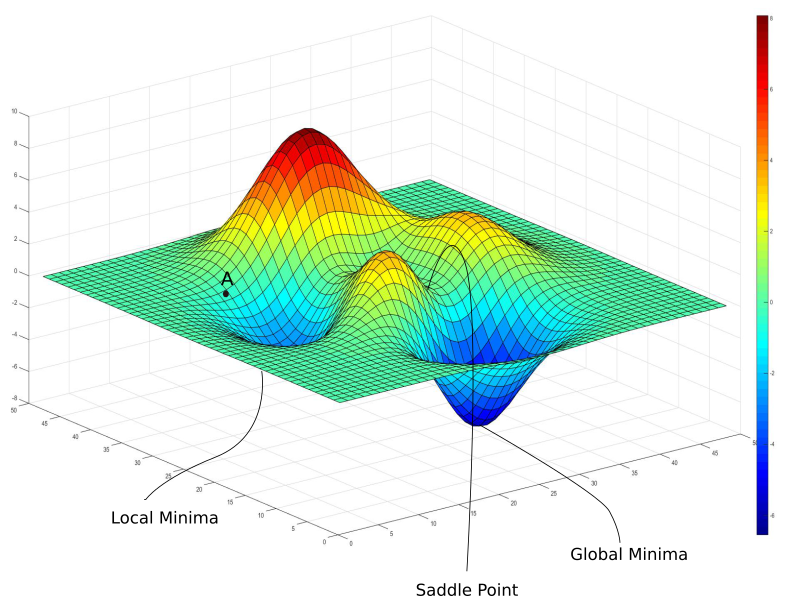
볼록 함수(Convex function)의 경우 어떤 점에서 시작해도
적절한 학습률(Learninig Rate)와 학습횟수를 사용하면 항상 최소값으로 수렴할 수 있지만
우리가 문제해결 시 마주하는 대부분의 함수는 비볼록 함수(non-Convex function)이기 때문에 문제가 생긴다.
A에서 경사하강법을 시작하게 되면 Global Minimmum에 도달하기 전에
Local Minimum으로 수렴하고 그 후엔 해당 위치의 기울기가 0이기 때문에 빠져나올 수 없다.
또한 안장점은 기울기 값이 0이지만 극값은 아닌 지점인데
이 역시 목표가 아닌 곳에서 빠져나올 수 없으므로 문제가 된다.
이런 문제점을 해결하기 위해 다양한 기법이 사용된다.
ex. Momentum, Adam, AdaGrad 등.
질문 3. Learning rate는 어떤 역할을 할까?
Learning rate는 step size라고 하기도 하는데
말 그대로 경사하강법 사용 시 얼만큼 움직이는지 정해주는 역할이라고 보면 된다.
Learning rate를 적절한 크기로 설정하는 것이 중요한데 그 이유는,
너무 크면 최솟값을 찾지 못하고 발산해버리고
너무 작으면 학습시간이 지나치게 길어지고 수렴을 못할 수 있기 때문이다.
작성에 도움이 된 사이트 및 자료 👍


