review
지난 포스트에서는 MOSFET의 특징과 BJT의 차이점에 관해서 공부했다. 이번 포스트에서는 그것을 기반으로 MOSFET, 특히 pMOS와 nMOS의 특징과 소자를 이용하여 회로를 구성해 논리게이트(NOT, 2NAND, 2NOR)를 만들어 볼 것이다.
nMOS와 pMOS, 넓이(Width)-길이(Length)
nMOS와 pMOS의 차이는 Source부와 Drain부의 N형-N형, P형-P형 반도체가 다름도 들 수 있지만, 중요한 차이가 하나 더 존재한다. 바로 hole과 electron의 drift 속도가 다르기에 나타나는 현상이다. 따라서 지난 포스트에서 언급했던 MOSFET의 수치에서, 같은 Width과 length를 설정한 pMOS, nMOS라 할지라도 운반자의 속도 차이 때문에 오류(베타값과 다름)를 출력하게 된다.
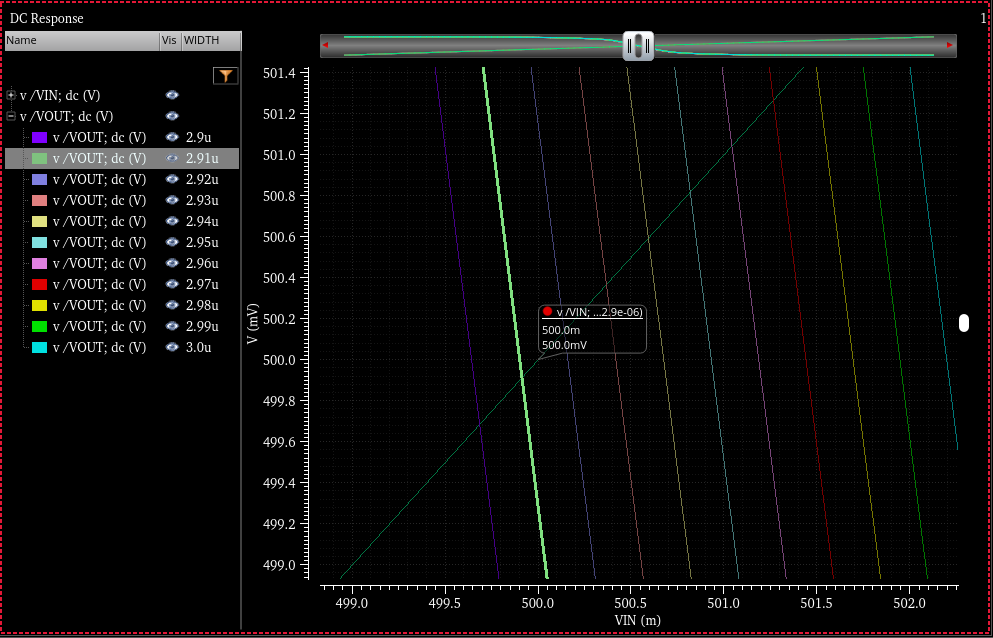
따라서 적절한 베타값을 찾기 위해 시뮬레이션을 통해 소숫점 둘째 자리까지 내려가면서 WIDTH값을 계산하여 적확한 값을 발견하여 pMOS의 값을 선정한다.
Simulation
다음은 시뮬레이션을 통한 pMOS의 Width값을 찾는 과정이다.
Schematic을 먼저 구성한 후, 1µm~10µm로, 1µm씩 변경해가면서 계산한 후, 스케일을 0.1로 변경하여 2번 더 시행한다. 이를 통해 0.01µm의 정확도로 pMOS의 Width를 발견할 수 있다.
NOT 심볼
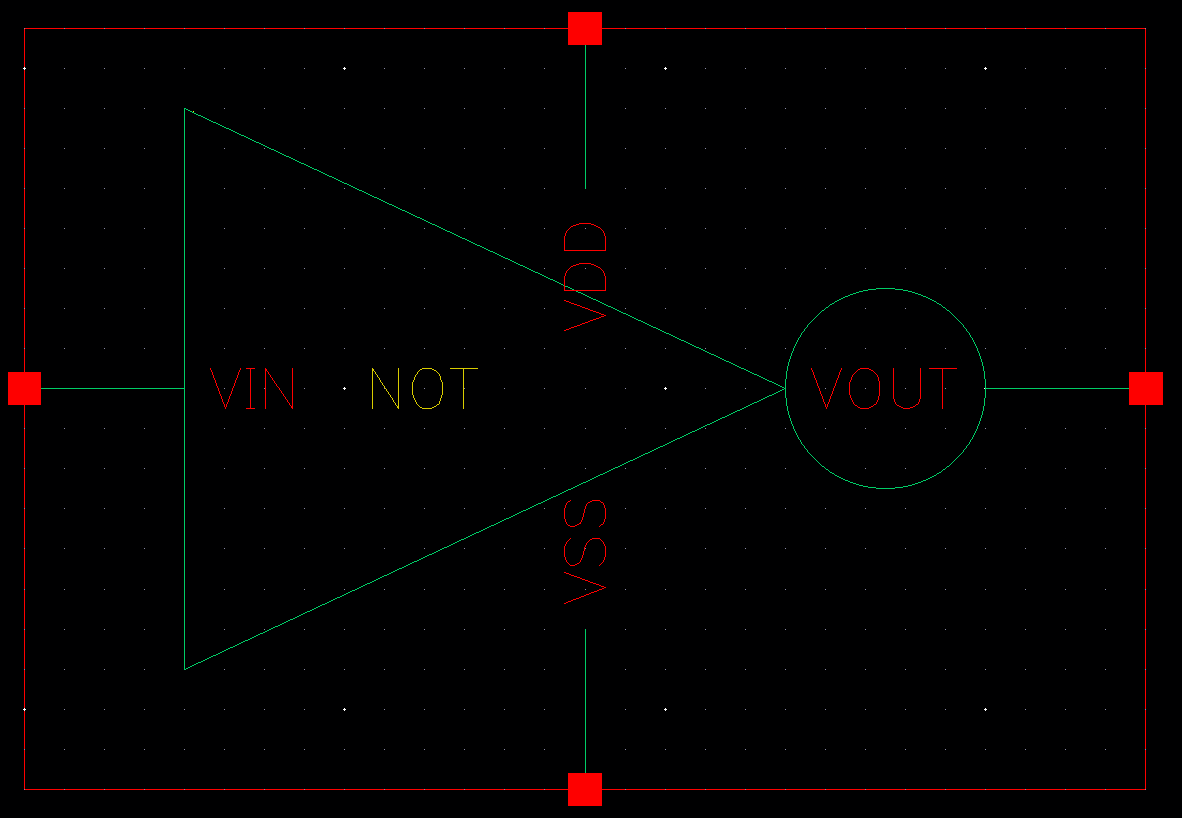
NOT 내부 회로
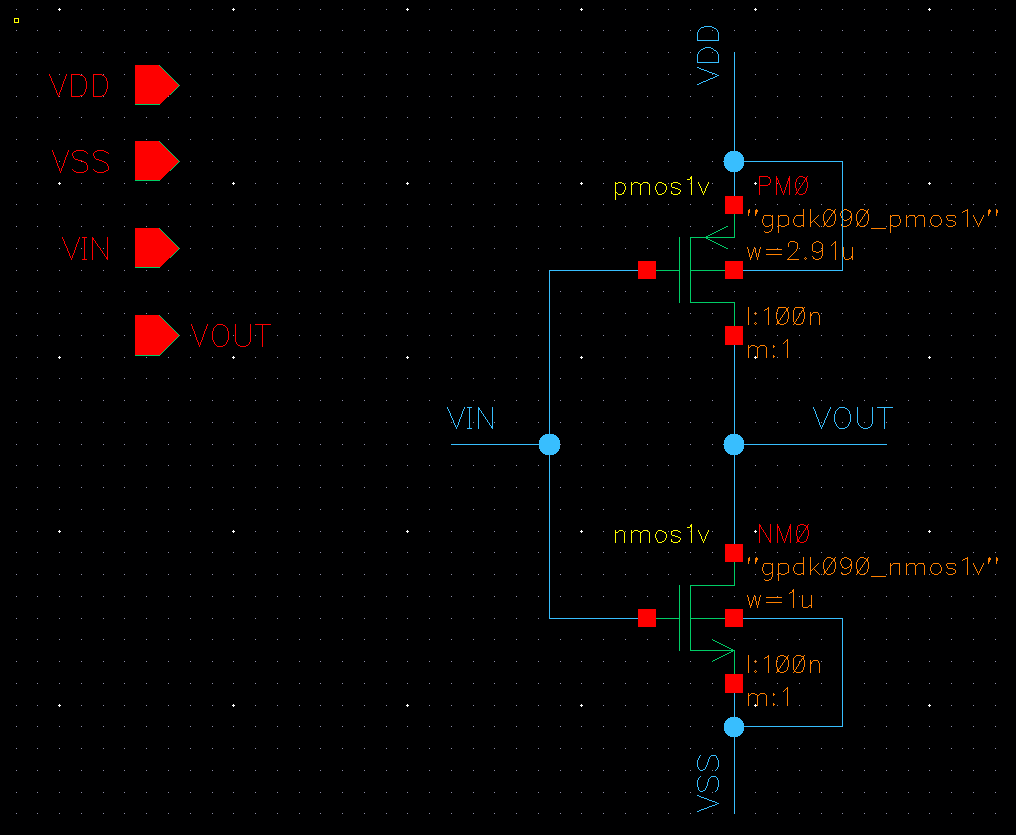
NOT NMOS-PMOS 베타값
2NAND 심볼
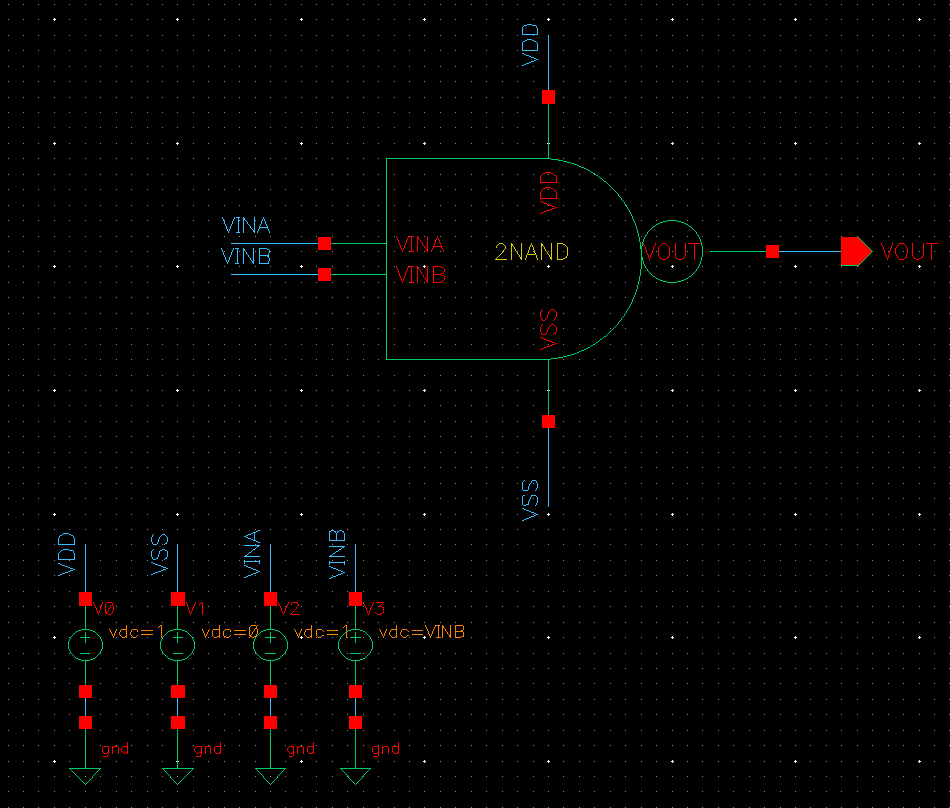
2NAND 내부 회로
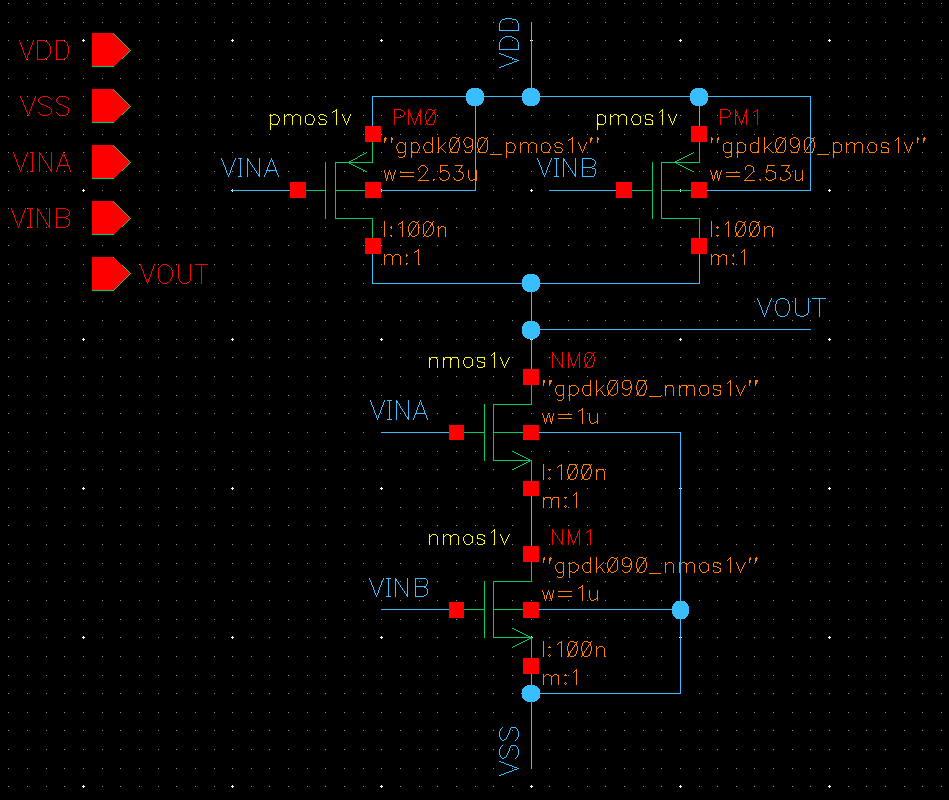
2NAND NMOS-PMOS 베타값
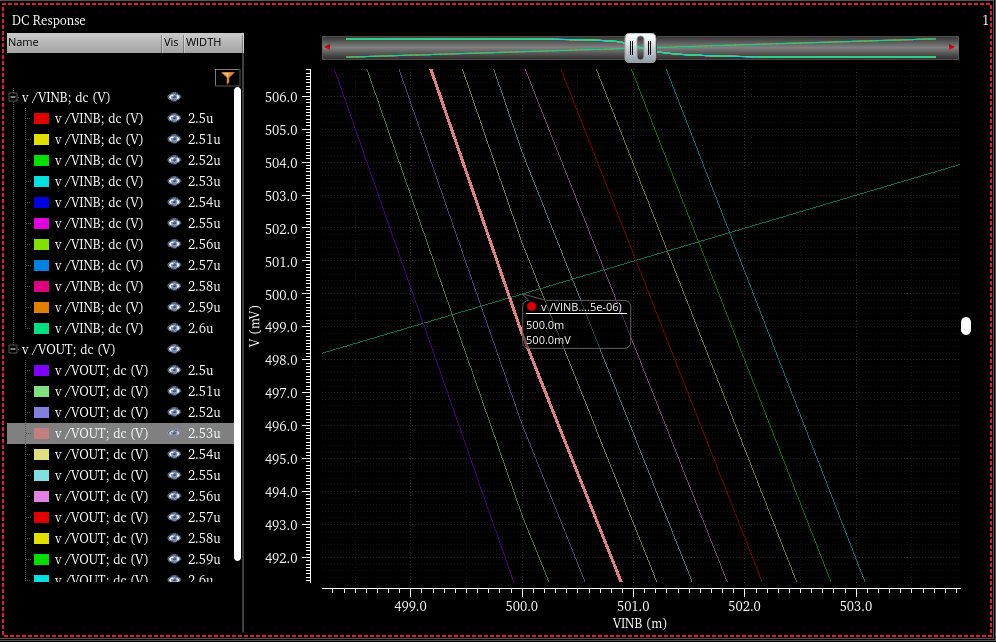
2NOR 심볼
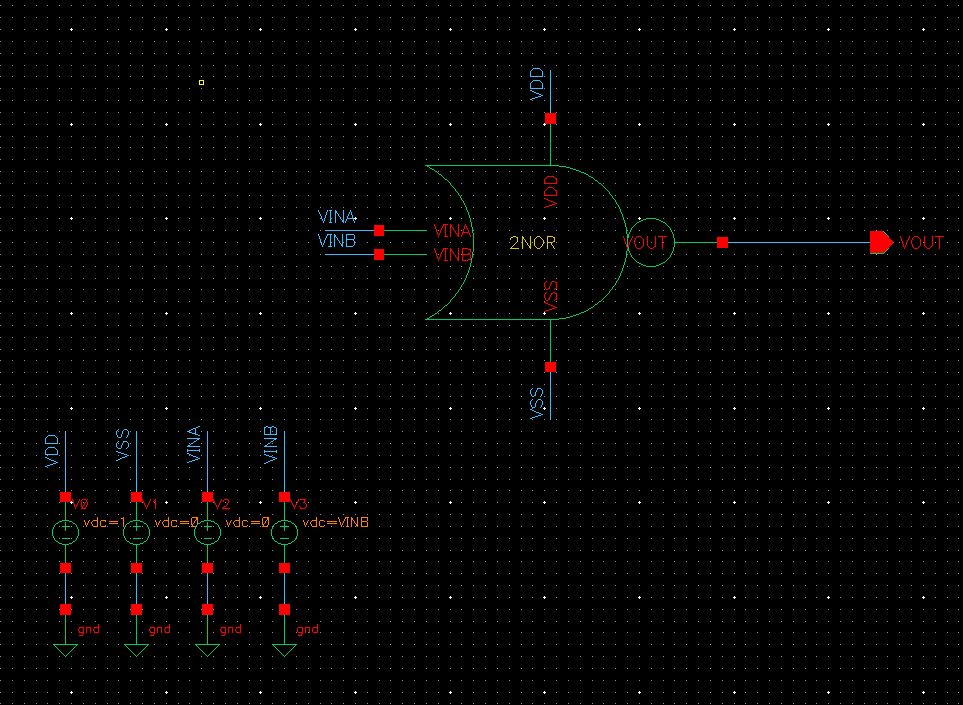
2NOR 내부 회로
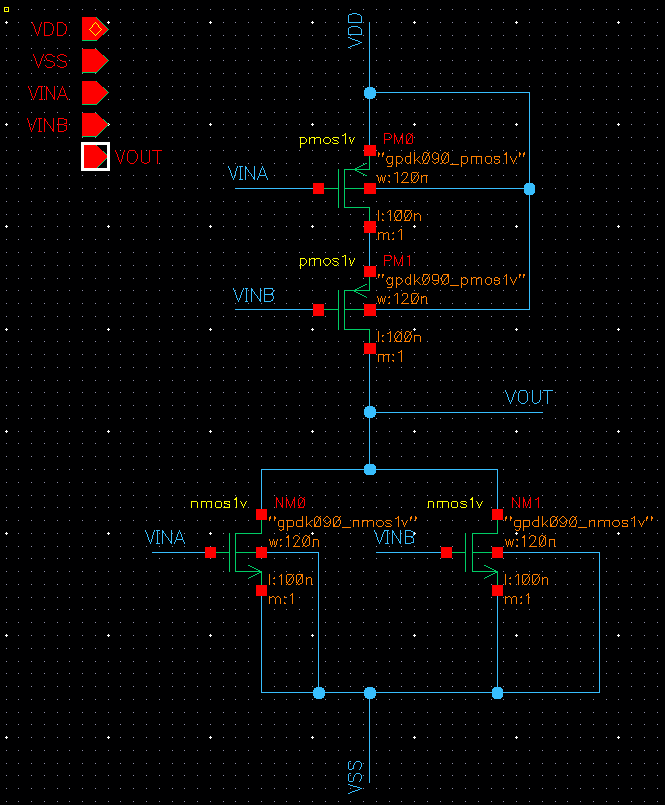
2NOR NMOS-PMOS 베타값
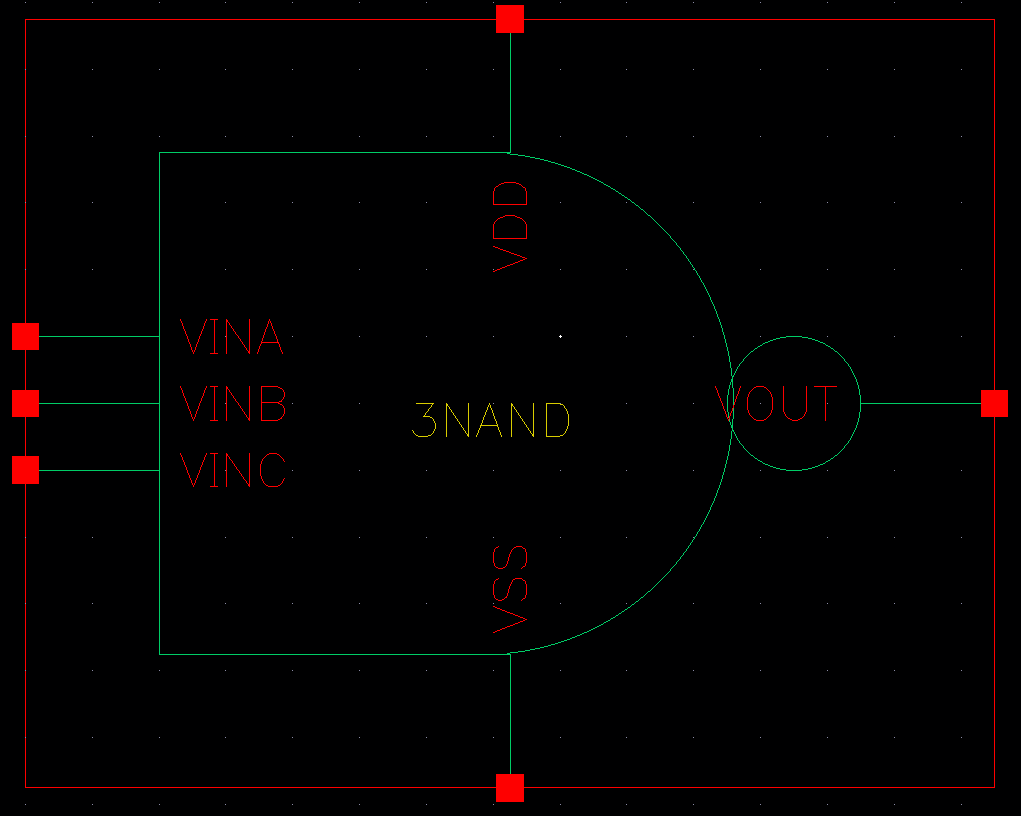
3NAND 심볼
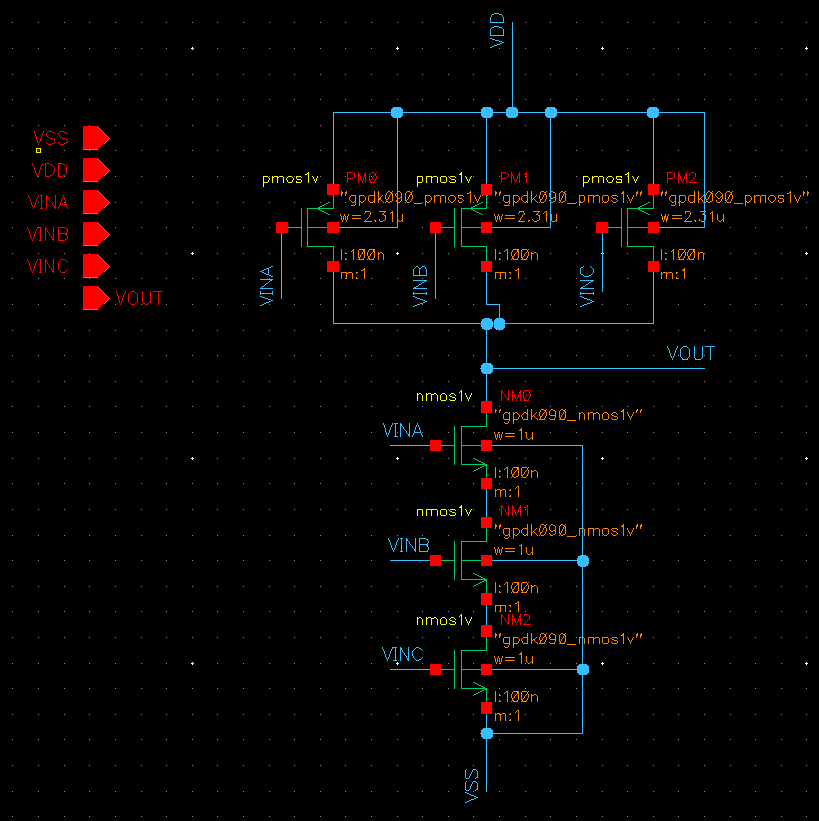
3NAND 내부 회로
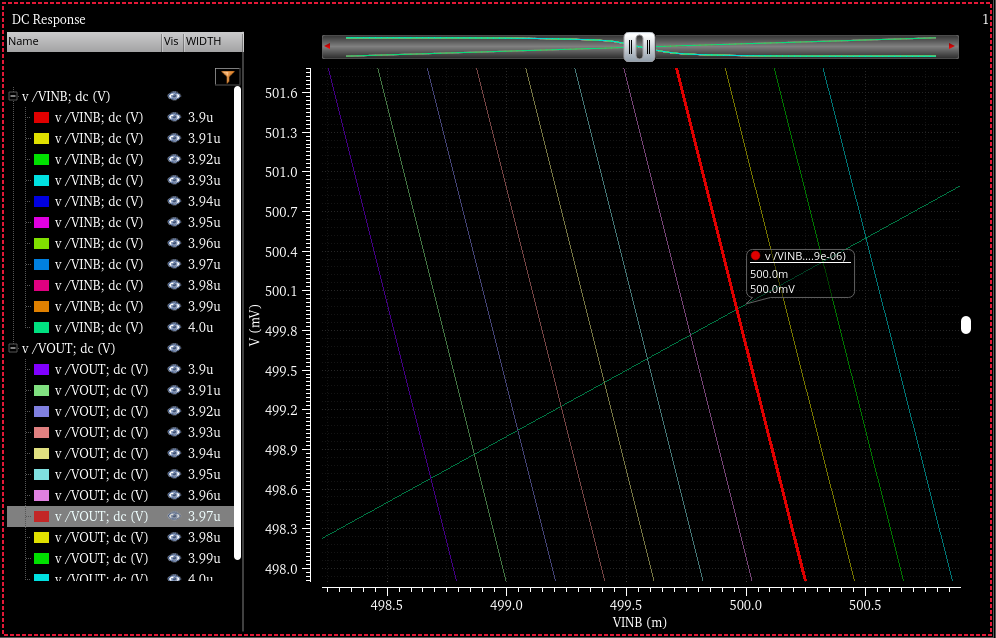
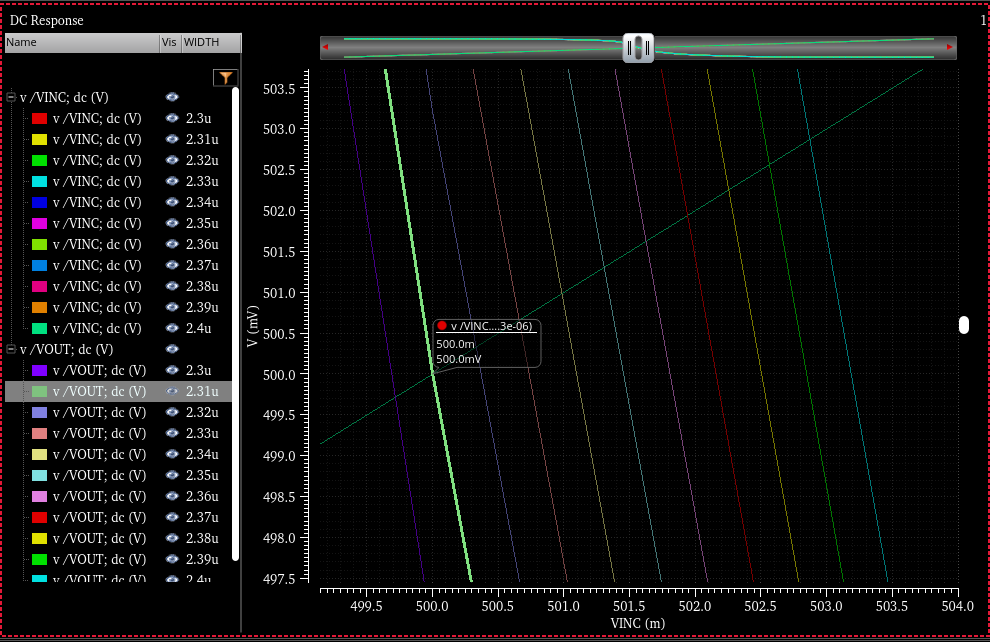
3NAND NMOS-PMOS 베타값
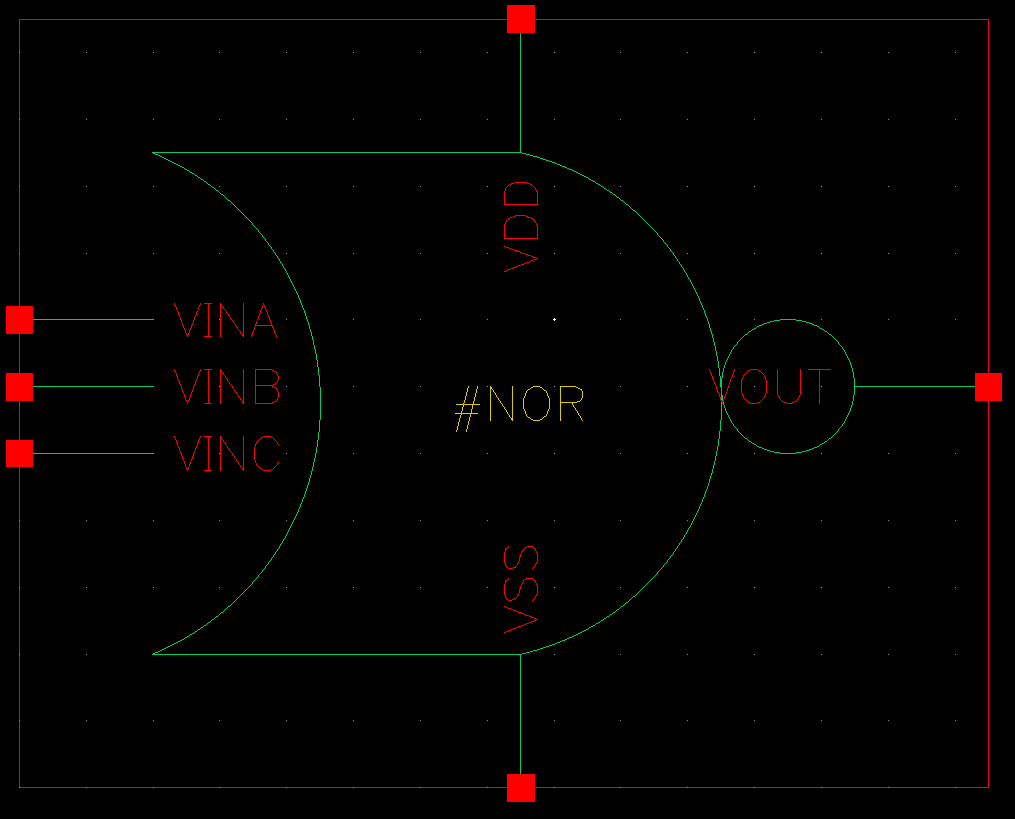
3NOR 심볼
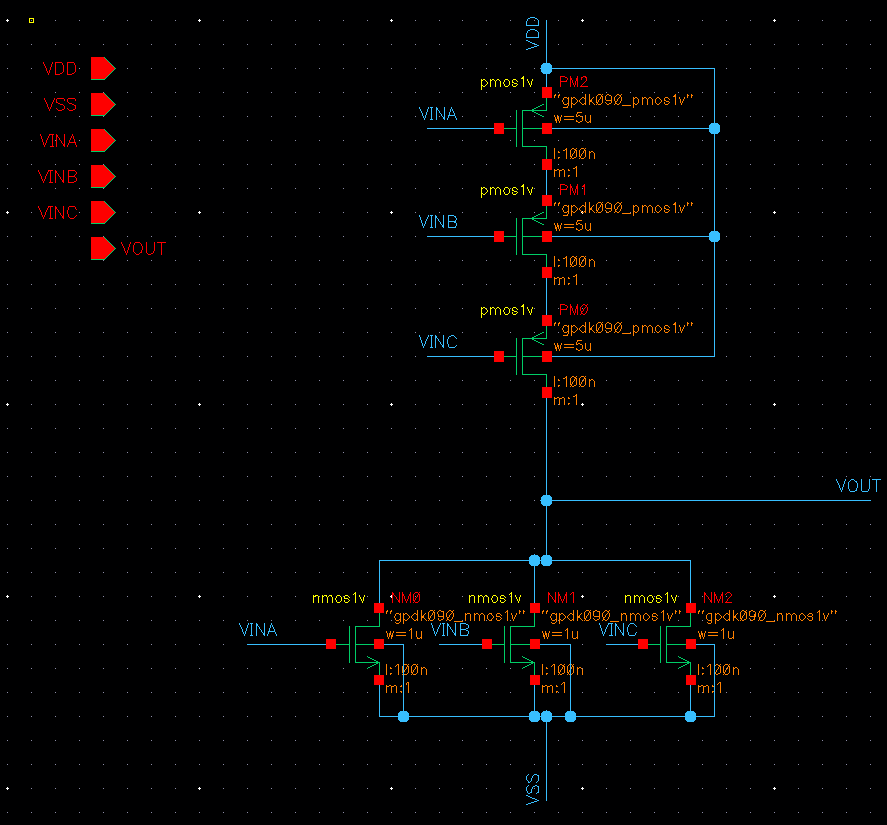
3NOR 내부 회로
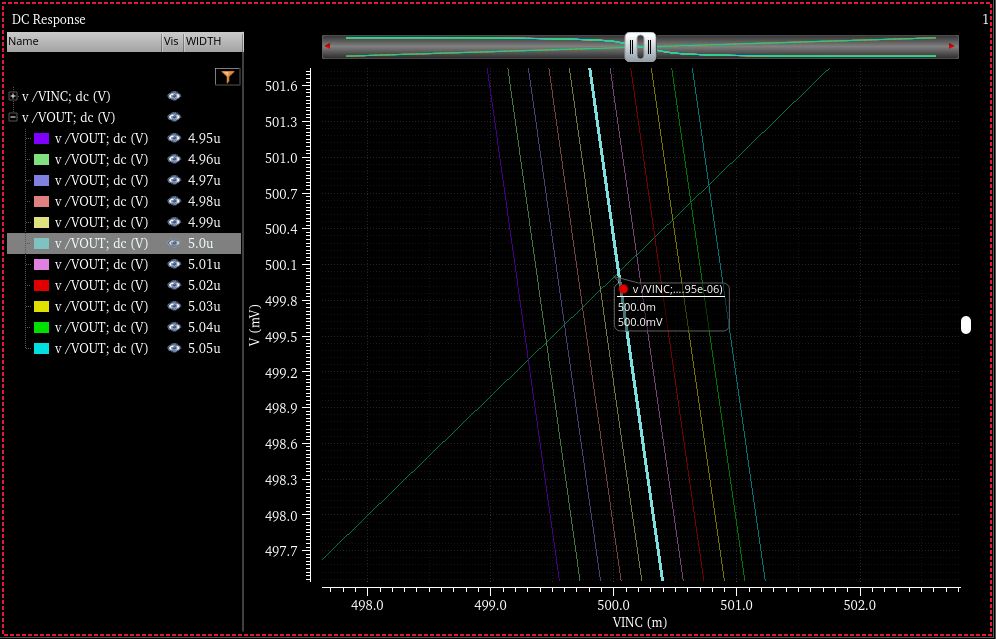
3NOR NMOS-PMOS 베타값
| 논리 게이트 | NOT | 2NAND | 2NOR | 3NAND | 3NOR |
|---|---|---|---|---|---|
| FET 개수 | 2 | 4 | 4 | 6 | 6 |
| 베타값 | 2.91µm | 2.53µm | 3.97µm | 2.31µm | 5.00µm |
표에서, 논리게이트들 종류마다 Width가 모두 다르다. NAND의 pMOS들은 병렬 개수가 증가할 때마다 Width 값이 줄어들고, NOR의 pMOS들은 직렬 개수가 증가할 때마다 Width가 증가함을 알 수 있다.
논리 게이트에서 nMOS와 pMOS 각 파트 두 종류가 모두 같은 저항을 가지고 있어야 한다.
NAND 게이트의 경우, 어떤 입력 하나라도 ON 되어있다면, 출력이 ON 되기에 pMOS 중에 하나만 저항을 충족시키면 되므로 전체의 저항이 하나와 같지만, nMOS는 직렬로 연결되었기 때문에 개수만큼 나눠서 저항을 분담한다. 예를 들어, 3NAND의 경우엔, nMOS 3개가 저항을 3분할하기 때문에 하나의 nMOS에 전체 저항의 3분의 1이 걸리지만, pMOS의 경우, 전체 저항과 pMOS 하나의 저항이 같게 나타난다.
NOR의 경우, NAND게이트와 반대로 pMOS가 직렬로 연결되어 모든 입력이 off되어야 출력에서 on 되므로 저항을 모두 나눠 갖는다. 따라서 직렬 연결이 증대될수록 pMOS 파트의 총 저항이 증가하게 되므로, W를 증가시켜서 베타값을 찾게 된다.
꽤나 복잡한 글이 되었지만, nMOS의 운반자 electron이 pMOS의 운반자보다 빠르다는 것만 기억하면, 순차적으로 이해할 수 있다는 점이 이번 포스트의 포인트라고 생각한다.
