카운터의 추가 확장
지난 포스트에서는 4비트 가산기의 차이점과 그 연산 방식, 그리고 시간과 사용 자원에 대해 비교해봤다. 이번 포스트에서는 4비트 가산기를 확장하여 16비트 가산기를 제작하고, 한가지 연산 방식을 추가하여 3가지 고속연산 방식을 비교해보려고 한다.
RCA16
지난 번에 사용한 RCA4를 직렬 연결하여 carry들을 연속으로 받아 연산하는 4개의 조합회로의 묶음이다. 총 16bit를 연산한다.
module RCA_16bit (a, b, cin, s, cout);
input [15:0] a, b;
input cin;
output [15:0] s;
output cout;
wire [4:0] tc;
assign tc[0] = cin;
RCA_4bit U0 (a[3:0], b[3:0], tc[0], s[3:0], tc[1]);
RCA_4bit U1 (a[7:4], b[7:4], tc[1], s[7:4], tc[2]);
RCA_4bit U2 (a[11:8], b[11:8], tc[2], s[11:8], tc[3]);
RCA_4bit U3 (a[15:12], b[15:12], tc[3], s[15:12], tc[4]);
assign cout = tc[4];
endmoduleTest Bench
`timescale 1ns / 1ps
module TB_RCA_16bit;
reg [15:0] a, b;
reg cin, clk;
wire [15:0] s;
wire cout;
RCA_16bit_FF U0 (a, b, cin, clk, s, cout);
always #5 clk = ~clk;
initial begin
clk = 0 ;
a = $urandom(); b = $urandom(); cin = $urandom(); #100;
a = $urandom(); b = $urandom(); cin = $urandom(); #100;
a = $urandom(); b = $urandom(); cin = $urandom(); #100;
end
endmoduleSchematic(RSC16_bit)
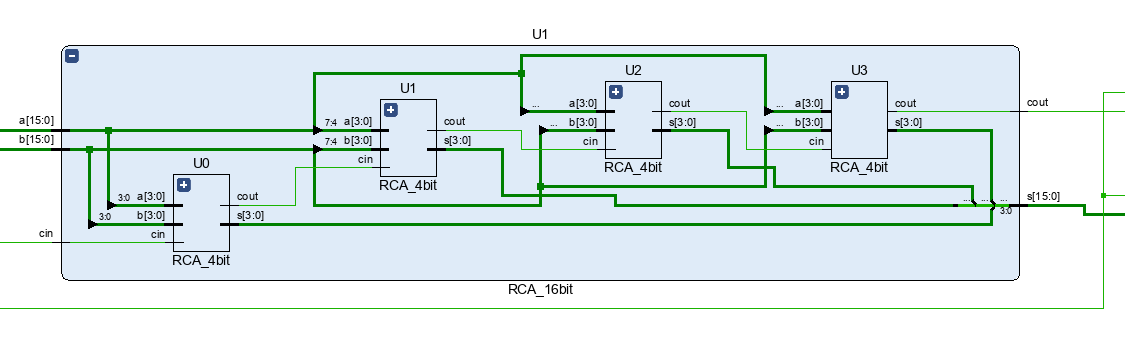
결과

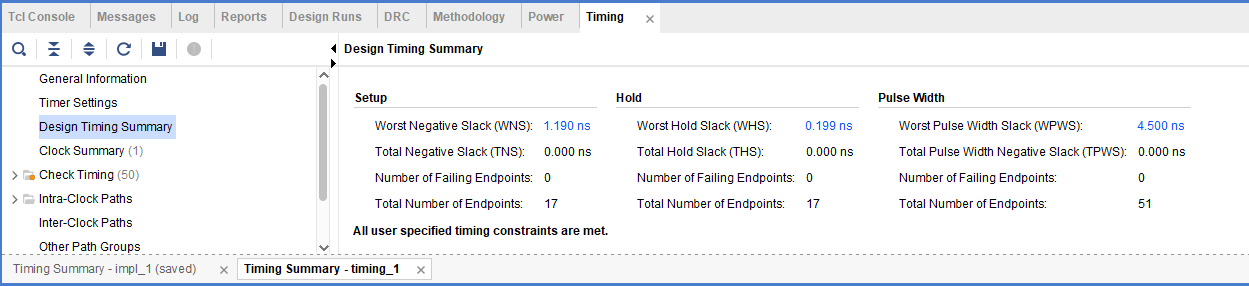
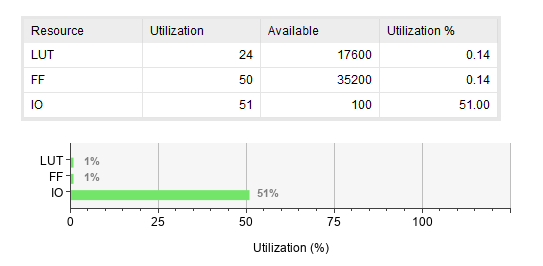
GCLA16
모든 입력을 동시에 연산하다 보면, 회사에서 제공하는 논리 게이트의 라이브러리에 일정 이상의 입력을 받을 수 있는 논리 게이트가 존재하지 않고, layout에서 그 논리 게이트는 너무나도 커지게 된다. 따라서 CLA를 4개 연결하여, 그륩화한 Sum과 cout을 사용하면 각 4bit 단위의 연산을 빠르게 진행할 수 있다. 그러나, 추가적인 모듈과 CLA 특유의 많은 면적과 전력을 사용하는 단점이 있다.
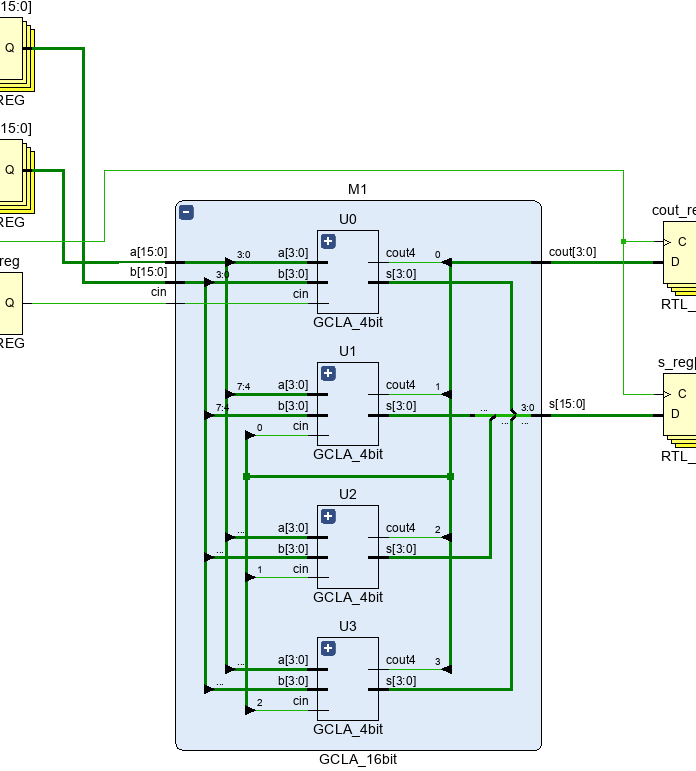
module GCLA_16bit (a, b, cin, cout, s);
input [15:0] a, b;
input cin;
output [3:0] cout;
output [15:0] s;
wire [3:0] tc;
wire [15:0] st;
GCLA_4bit U0(.a(a[3:0]), .b(b[3:0]), .cin(cin), .cout4(tc[0]), .s(st[3:0]));
GCLA_4bit U1(.a(a[7:4]), .b(b[7:4]), .cin(tc[0]), .cout4(tc[1]), .s(st[7:4]));
GCLA_4bit U2(.a(a[11:8]), .b(b[11:8]), .cin(tc[1]), .cout4(tc[2]), .s(st[11:8]));
GCLA_4bit U3(.a(a[15:12]), .b(b[15:12]), .cin(tc[2]), .cout4(tc[3]), .s(st[15:12]));
assign cout = tc;
assign s = st;
endmodule 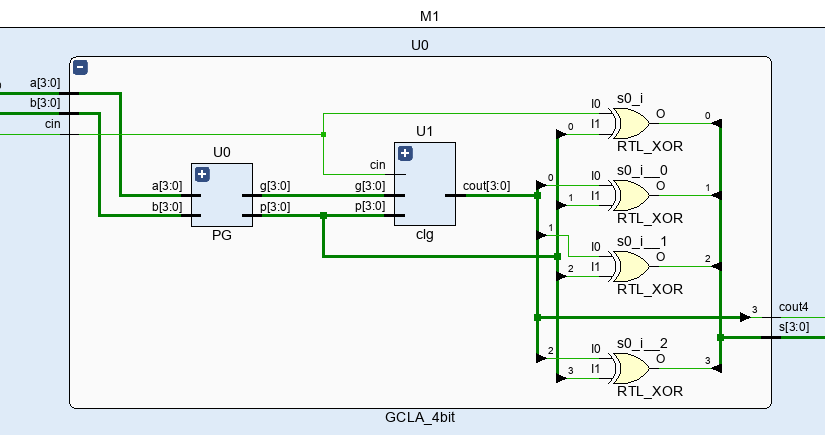
module GCLA_4bit(a, b, cin, cout4, s);
input [3:0] a, b;
input cin;
output cout4;
output [3:0] s;
wire [3:0] p, g;
wire [3:0] tc;
PG U0 (a, b, p, g);
clg U1 (p, g, cin, tc);
assign s[0] = cin ^ p[0];
assign s[1] = tc[0] ^ p[1];
assign s[2] = tc[1] ^ p[2];
assign s[3] = tc[2] ^ p[3];
assign cout4 = tc[3];
endmodule
결과
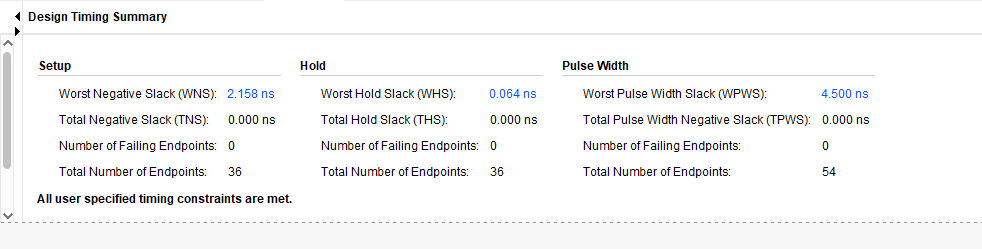
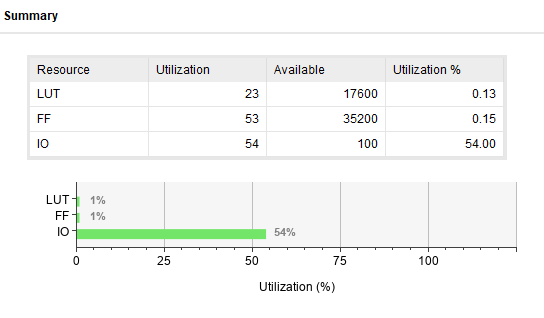
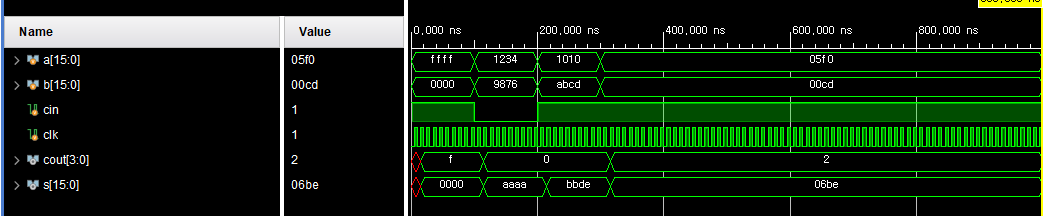
CSA16 (Carry Select Adder)
CSA은 RSA와 CLA 두 가지 방식 모두 하위모듈로 적용할 수 있는 연산기이다. Select라는 MUX 모듈을 사용하며, select 내부에서 RSA나 CLA 모듈을 2개 사용, cin이 0 또는 1일 상황을 미리 전제하여 연산한 이후, 그 값을 저장하고 있다가 이전 4bit 연산이 오면 그것으로 미리 연산한 값을 선택 출력한다. 다른 모듈보다 훨씬 빠르고, 이전 연산이 끝나기를기다릴 필요는 없지만 많은 면적과 전력을 소모한다는 단점이 있다. 다음은 CSA16의 Schematic이다.
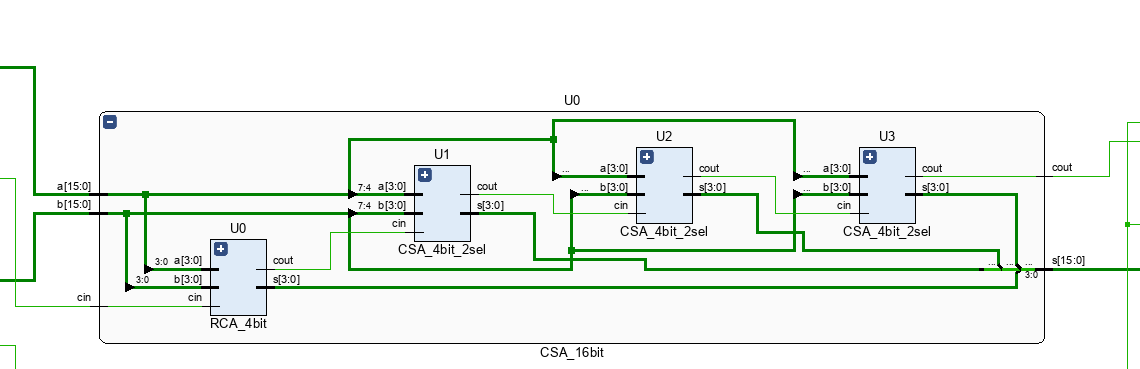
sel
내부 sel 모듈이다. 최초 4bit에서는 선택 연산이 필요가 없으므로, 일반적인 RSA나 CLA를 사용한다. 이 모듈은 RSA를 사용했다.
module CSA_4bit_2sel(a, b, cin, s, cout);
input [3:0] a, b;
input cin;
output wire [3:0] s;
output wire cout;
wire [3:0] s0, s1;
wire [1:0] cout_sel;
RCA_4bit U0 (a, b, 1'b0, s0, cout_sel[0]);
RCA_4bit U1 (a, b, 1'b1, s1, cout_sel[1]);
assign s[0] = cin ? s1[0] : s0[0];
assign s[1] = cin ? s1[1] : s0[1];
assign s[2] = cin ? s1[2] : s0[2];
assign s[3] = cin ? s1[3] : s0[3];
assign cout = cin ? cout_sel[1] : cout_sel[0];
endmodule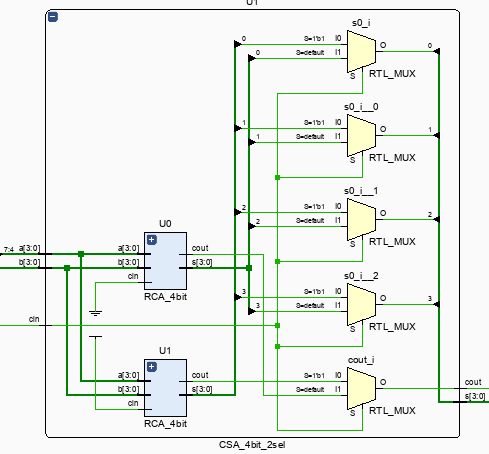
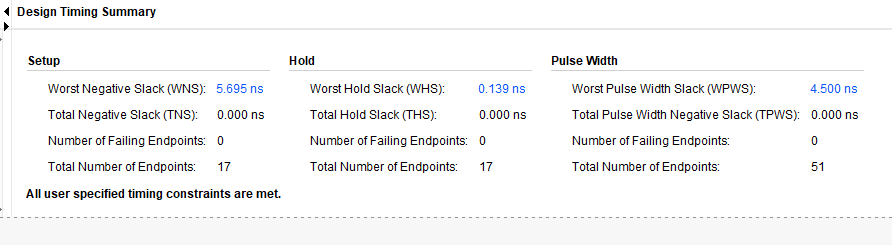
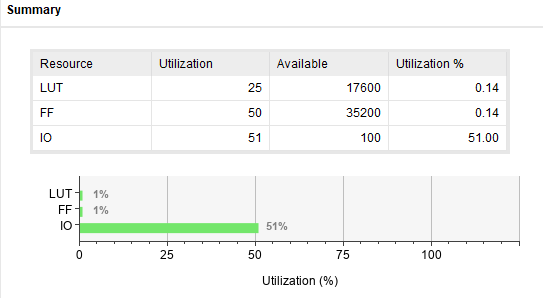
결과

정리
| RCA16 | GCLA16 | CSA16 | |
|---|---|---|---|
| 시간 | 9.009ns | 7.906ns | 4.444ns |
| I/O(LUT) | 51%(24) | 54%(23) | 51%(25) |
표를 보면, 각 가산기들이 각기 장단점이 있음을 알 수 있다. 따라서 우리는 회로를 설계할 때 속도를 중시할 것인지, 면적과 자원을 소모하는 것을 줄일 것인지 신중하게 선택해서 설계해야만 함을 알 수 있다.
