[ML] Basic of Regression

Regression

예제로 이해하기

- 주택가격 예측하기

• 주택에 대한 정보를 바탕으로 예측을 한다면?
• 연속된 값으로 예측 하는 것을 회귀 문제라고 함

- 모델 만들기

• 첫 번째 : Linear 하다는 가정으로 시작!
  

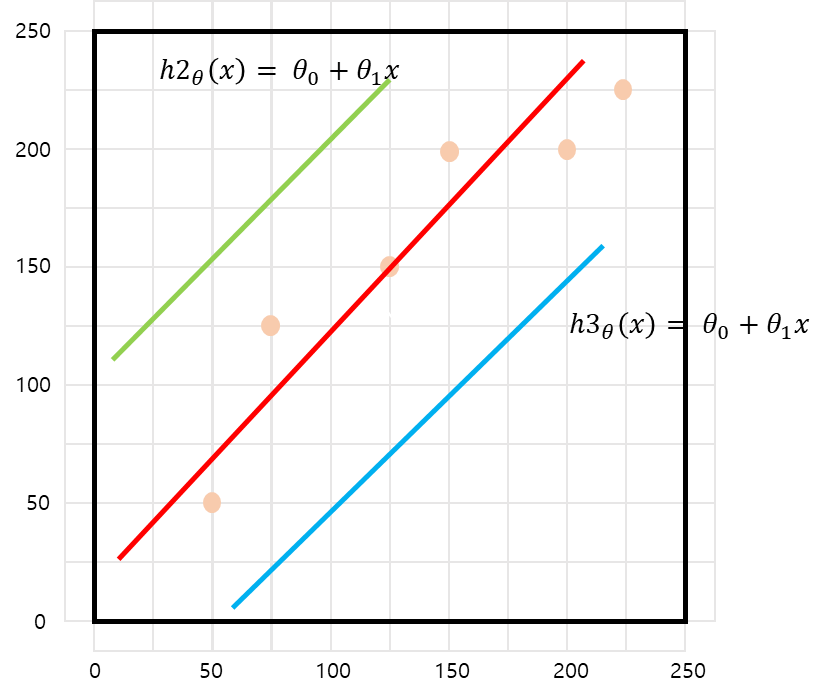
• 두 번째 : $hn_{\theta} -y$ 가 최소가 되는 $\theta_0$ 과 $\theta_1$ 를 찾는 과정 (Cost Function)
  

              - Learning Algorithmn : 파라미터, 하이퍼파라미터를 찾는 과정이라고 생각하면 된다(?)
              - hypothesis : 우리가 Linear 하나도 가설을 세우는 것
              

OLS : Ordinary Linear Least Square

• 아래와 같은 직선이 있다
  

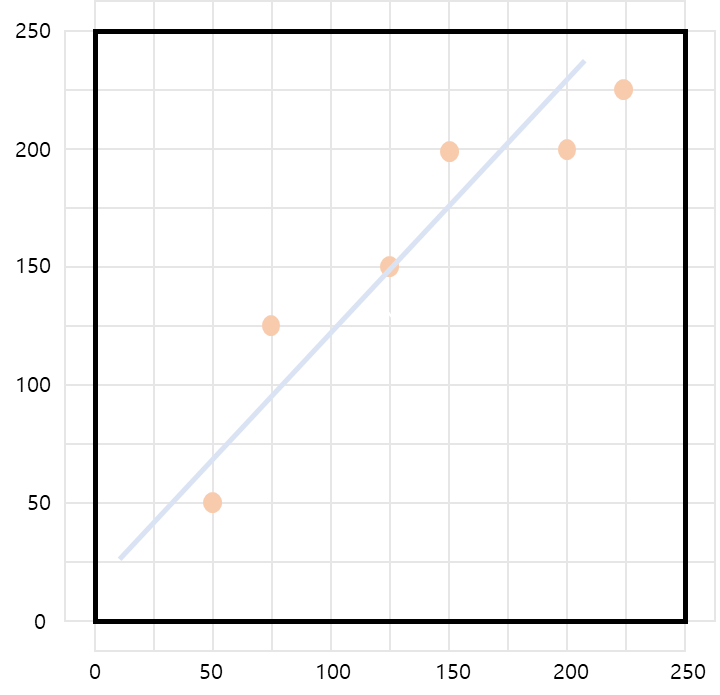
• 직선에 데이터를 대입한다

  $y_1 = ax_1 + b \\\ y_2 = ax_2 + b \\\ y_3 = ax_3 + b \\\ y_4 = ax_4 + b \\\ \vdots\\\ yn = ax_n + b$

  $$

• a와 b를 구해야한다

• 벡터와 행렬로 표현

  $Y =AX,\ Y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} , A = \begin{pmatrix} x_1 &1\\ x_2 &1 \\ \vdots & \vdots \\ x_n &1 \end{pmatrix} , X= \begin{pmatrix} a \\ b \end{pmatrix}$

• 전치 행렬을 이용해 정리

  $A^TAX=A^TY$

• 역행렬 계산

  $(A^TA)^{-1}(A^TA)X=(A^TA)^{-1}A^TY \\ X = (A^TA)^{-1}A^TY$

  $$

• 마지막 형태는

  $X = \begin{pmatrix} a \\ b \end{pmatrix}$

• $a$ 와 $b$ 값이 나오므로 회귀식을 구할 수 있다

• 잔차의 최소를 찾는 것 즉, 모델의 성능을 나타낸다

  $E = \sum(y - \hat{y})$

Python 코드

- 데이터 만들기

data = {'x': [1.,2.,3,4,5],
        'y': [1,3,4,6,5]}

- 가설 세우기

• 회귀한다~

import statsmodels.formula.api as smf

lm_model = smf.ols(formula = 'y ~ x', data = df).fit()

• 'y ~ x' 는 $y = ax +b$를 의미

- 결과

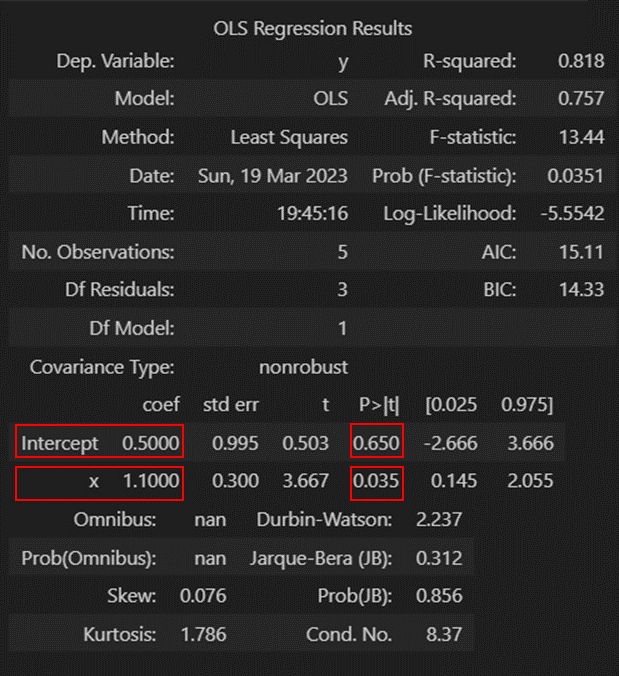
• intercept = $\alpha$ = $b$
• x = $\beta$ = $a$
• p-value 값을 보면 $x$ 는 통계적으로 유의

잔차 평가

- 선형회귀에서 잔차

• 회귀는 몇가지 가정을 하고 가는데 그중 잔차에 대한 두가지 가정을 알아봐야한다
• 첫 번째 : 잔차의 평균은 0이다
• 두 번째 : 정규분포를 따른다

- 잔차 확인

resid = lm_model.resid
resid

>>>
0   -0.6
1    0.3
2    0.2
3    1.1
4   -1.0

• 합이 0 이다!

- 결정계수 R-Squared

• 그림으로
  

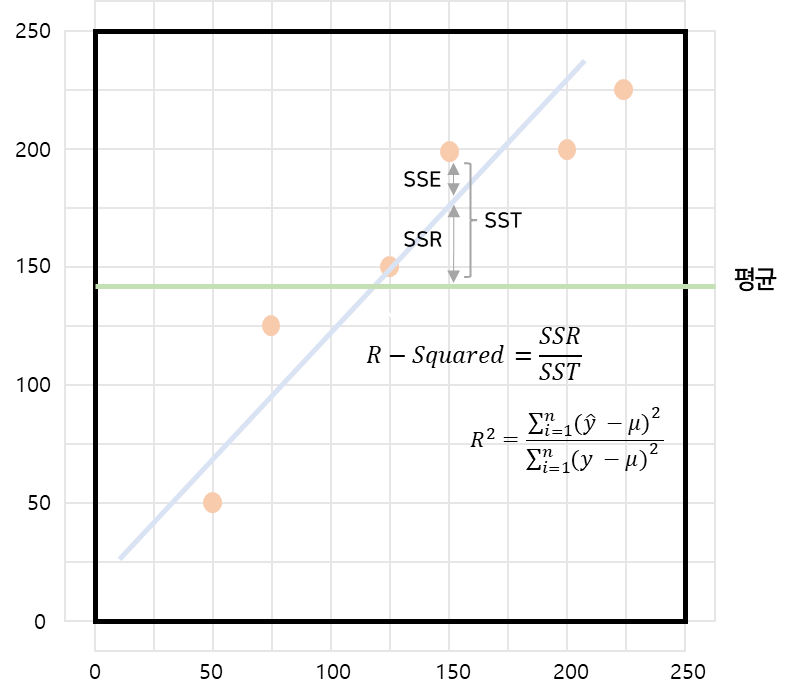
• Python

lm_model.rsquared

• 분포 확인

sns.distplot(resid, color='black');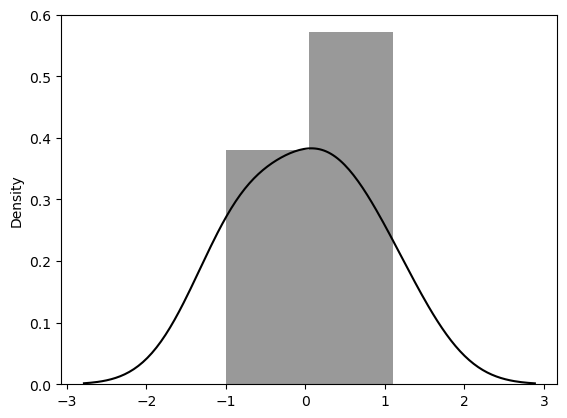

• 정규 분포 형태이다!

통계적 회귀와 머신러닝에서의 회귀

- 관계가 뚜렷한 그래프

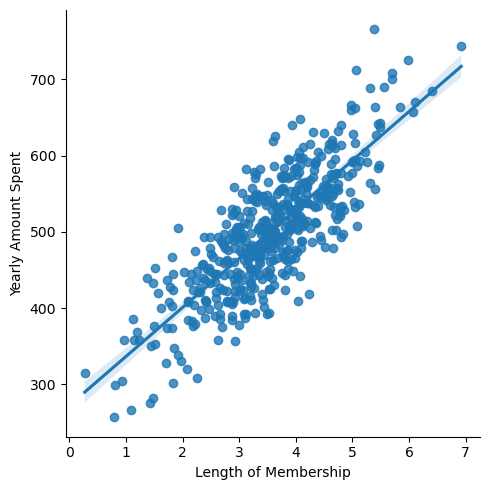
• 관계가 뚜렷한 데이터의 회귀직선

• 이 그래프를 OLS.summary() 를 보면 아래와 같다
  

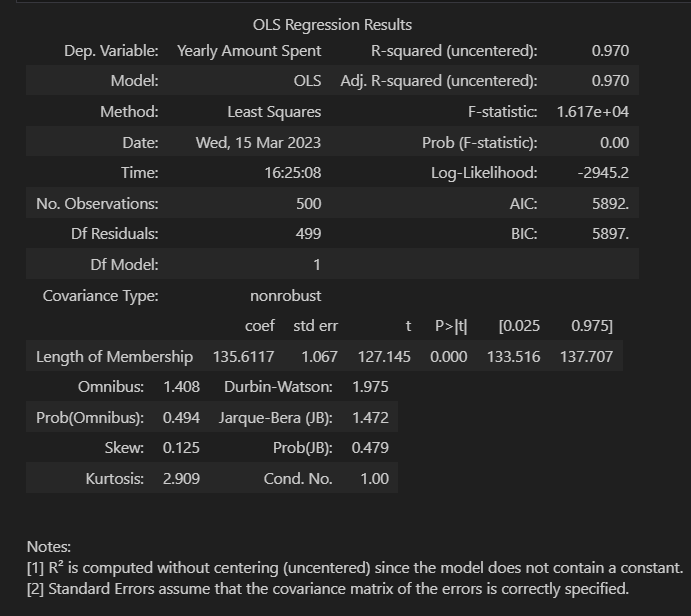
• R-Squared 값이 높다!

• 자유도 조정 결정계수 다중회귀분석에서 사용된다
  - 까먹었었는데 생각났다..!

• Prob. F-Statustuc 통계쩍 유의미성 검정
  - 0.05 이하라면 모집단에서도 의미가 있다고 볼 수 있다

• 참값과, 예측값을 찍은 그래프를 그려보면 상당히 다른 형태가 보인다..!

• 모델에 상수가 없어 중심값이 흔들리기 때문

- 상수항 넣어주기

X = np.c_[X, [1]*len(X)]

- 상수항 결과 확인

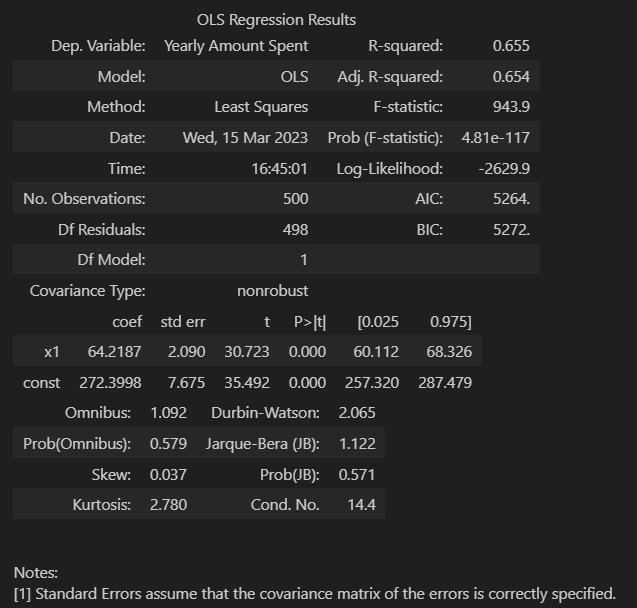
• AIC 값이 떨어졌다
  - 원본데이터의 손실양으로, 낮으면 낮을 수록 원본 데이터를 잘 반영 한 것
  

- 결론

• 결정계수가 중요한 역활을 하지만, 상수항을 고려하지 않아 원본데이터를 잘 반영하지 못하는 경우가 있다
• 따라서 잘 따져봐야 한다..?