[ML] Model Evaluation

- 모델 평가의 개념

• 모델이 얼마나 좋은 것일까 평가 할 방법이 없다
• 다양한 모델, 다양한 파라미터를 두고 상대적 비교

- 이진 분류 모델 평가

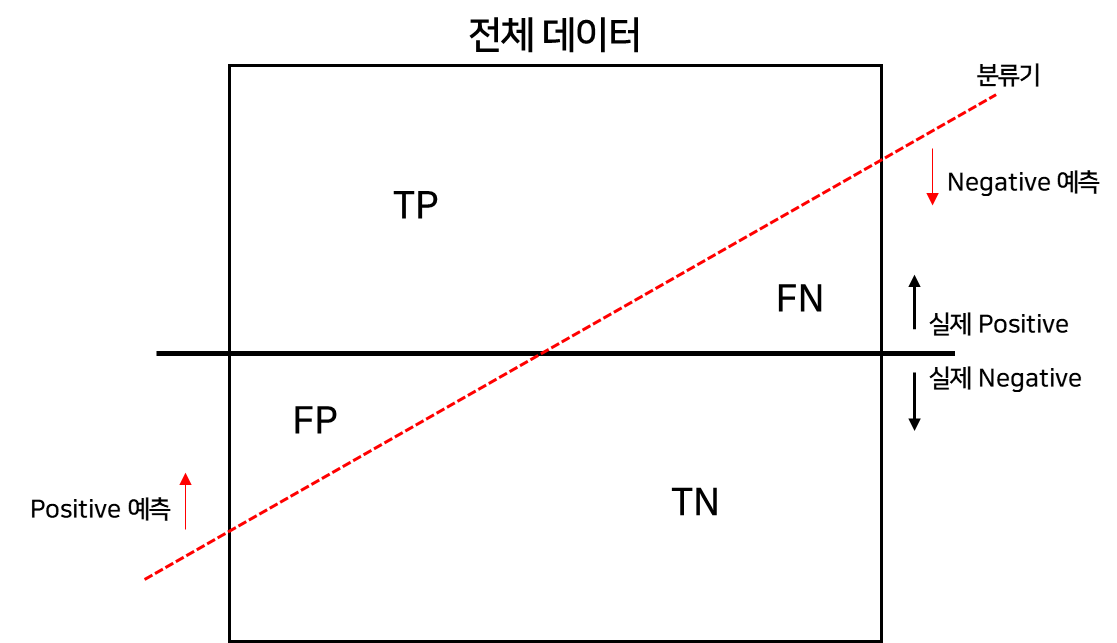
• 분류기 예시
  

• 앞에는 분류기를 맞췄냐 못맞췄냐 , True vs False

• 뒤에는 어떻게 예측 했냐 , Positive vs Negative

• 분류기 기준이다!

- Accuracy Score

• 정확도
• 전체 데이터 중 맞게 예측한 것의 비율

  $accuracy\ score ={TP + TN \over TP + TN + FP +FN }$

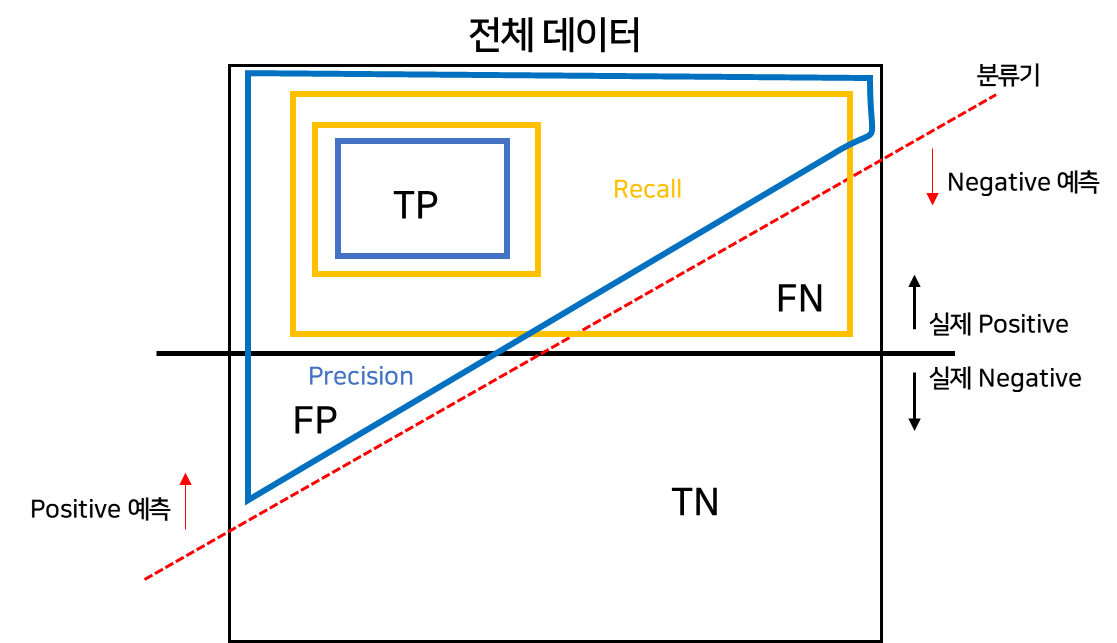
- Precision

• 정밀도
• Positive라고 예측한 것 중에 True 인 것

  $precision ={TP \over TP + FP}$

- Recall

• 재현율
• 실제 Positive 중에 True 인 것

  $recall ={TP \over TP + FN}$

- FAll-Out

• Positive 라고 잘 못 예측 한 것

  $recall ={FP \over FP + TN}$

- 정리

• 결과를 속할 확률을 반환한다

• default threshold 는 0.5 이고 변화를 시키는 것이 크게 의미 없다

• Recall 과 Precision 은 Trade-off 관계이므로 무엇을 판단하냐에 따라 중요하게 보는 기준을 다르게 해야한다.

• Recall : 실제 양성인 데이터를 음서이라고 판단하면 안되는 경우

• Precision : 실제 음성인 데이터를 양성이라고 판단하면 안되는 경우
  

• 조금 복잡해 보이는데 색깔로 기억하자..!!

- F1-Score

• 데이터가 복잡하면 형태가 이상하면 Recall - Precison 를 따지면 이상하게 된다
• 조화평균으로 Recall 과 PRecsion을 둘다 고려하여 점수를 낼 수 있다

  $F_\beta = (1 + \beta^2)(precision \times recall)(\beta^2precision + recall)$

• beta를 1로 두면 F1-score

  $F_1 = 2 \times precision \times recall / (precision + recall)$

  $$
• Recall , Precision 이 둘다 높은 값을 가질수록 높은 값을 가진다

ROC and AUC

• ROC 곡선
  

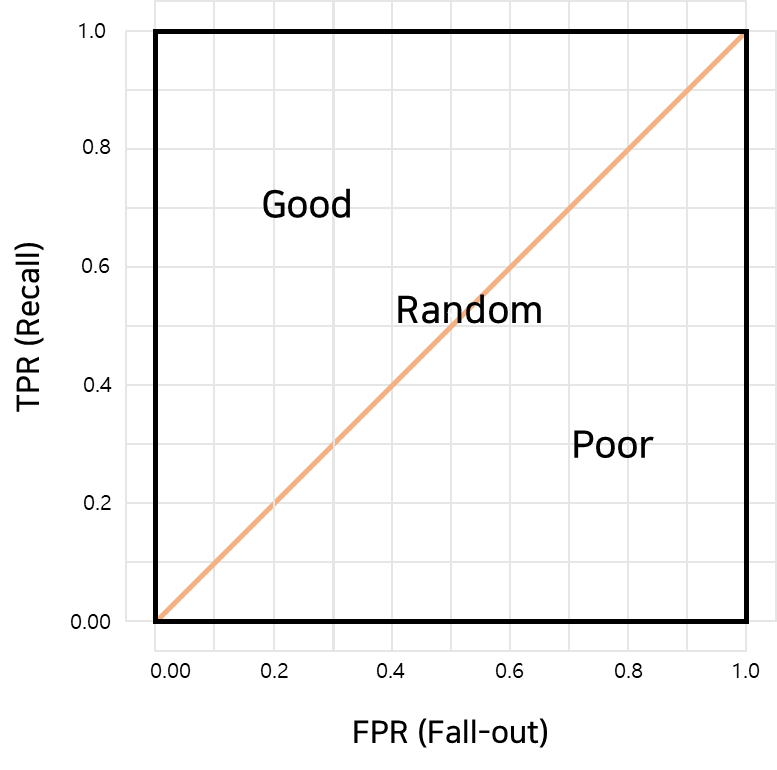
• 예를 들어보자
  위 그래프는 암환자를 받은 사람들이라고 생각하자.
  TPR은 True Positive 즉, 환자가 실제로 암이고, 암 판정을 받은 것이고
  FPR은 False Positive 즉, 암이라고 잘 못 판단 한 것이다.
  깔끔하게 정리를 못하겠다,,,
  다음 블로그를 참고하자..
  (참고 : https://angeloyeo.github.io/2020/08/05/ROC.html)

- 결론

• ROC 커브는 상단에 붙을 수록 좋은 그래프
• 그래프의 휨 정도는 그룹을 잘 구분 한다는 것
• 현 위의 점은 threshold
• AUC는 ROC 커브 아래 영역
• 즉, 넓으면 넓을수록 좋은 분류기 이다