[2022Kakao Blind] 파괴되지 않은 건물(Java)

---

문제

파괴되지 않은 건물

---

문제 해설

1 <= N,M <= 1,000이며 1 <= skill <= 250,000이기 때문에 일반적인 방법으로는 시간초과를 피할 수 없다. 가장 일반적으로 문제를 푸는 방법은 skill대로 2차원 배열을 일일이 탐색한 뒤, degree를 더해주는 방식인데 이 방법을 사용하면 O(n*m*k)의 시간이 걸리게 되며 효율성은 모두 틀리게 된다.

시간 복잡도를 줄이는 두 가지 방법

1. 구간 합과 1차원 배열을 이용하는 방법

board의 모든 요소가 1이며, degree = -2, r1,r2=2, c1,c2=3인 skill이 있다고 가정해보자

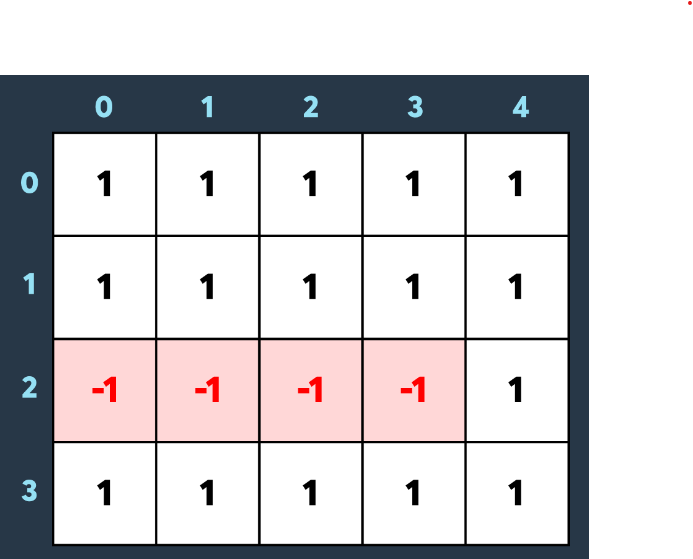
단순 행만(2행) 놓고 보자면, 구간 합을 다음과 같이 설정해줄 수 있다.

왼쪽 행부터 차례대로 더해주면 4열에는 0, 나머지는 -2가 되어 단순 2번의 계산만으로 구간 합을 저장할 수 있다.

하지만, 주어진 구간이 2차원이기 때문에 이 방법 역시 O(N*K)로 많은 시간을 먹게 된다.

2. 구간 합과 2차원 배열을 이용하는 방법
   1차원 배열을 이용하는 방법은 N의 행만큼 저장을 해야되기 때문에 오래 걸린 것이었다. 2차원 배열에 저장하는 방법을 사용하게 되면 4칸의 배열만으로 구간합을 저장할 수 있다. 저장 방법은 다음과 같다.

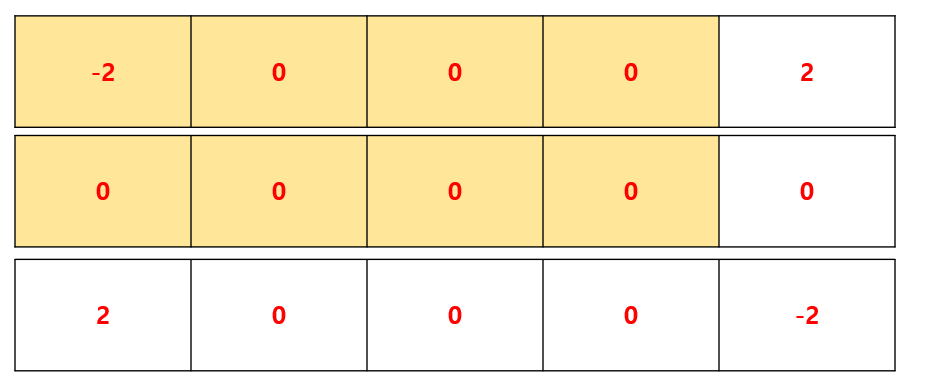
색칠한 부분의 구간 합을 구해야 한다면
r1,c1 = degree
r1,c2+1 = -degree
r2+1,c1 = -degree
r2+1,c2+1 = degree
에 값을 저장한 뒤, 위 -> 아래로 차례대로 계산 왼쪽 -> 오른쪽으로 차례대로 계산해주면 구간합을 구할 수 있다.

따라서, skill들을 모두 순회하고(O(n) = K) 구간합을 저장하며(O(n) = 1) 구간합을 차례로 계산(O(n) = n*m)해주면 시간 내로 문제를 해결할 수 있을 것이다.

---

풀이 코드

class Solution {
    public int solution(int[][] board, int[][] skill) {
        int answer = 0;
		// n,m 값 설정
		int n = board.length, m = board[0].length;
		// 누적 합을 가질 2차원 배열 설정, 끝점 표기를 위해 1칸씩 늘려준다.
		int[][] mem = new int[n + 1][m + 1];
		// 1. skill을 받아 누적합에 저장한다.
		for (int[] s : skill) {
			int type = s[0], r1 = s[1], c1 = s[2], r2 = s[3], c2 = s[4], degree = s[5];
			degree = s[0] == 2 ? s[5] : -s[5];
			mem[r1][c1] += degree;
			mem[r2 + 1][c1] += -degree;
			mem[r1][c2 + 1] += -degree;
			mem[r2 + 1][c2 + 1] += degree;
		}
		// 2. 누적합을 계산한다.
		// 2-1. 상하
		for (int i = 0; i < m; i++) {
			for (int j = 1; j < n; j++) {
				mem[j][i] += mem[j - 1][i];
			}
		}
		// 2-2. 좌우
		for (int i = 0; i < n; i++) {
			for (int j = 1; j < m; j++) {
				mem[i][j] += mem[i][j - 1];
			}
		}
		// 3. 계산된 누적합과 기존 board를 더해 건물을 확인한다.
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				if (board[i][j] + mem[i][j] > 0)
					answer++;
				board[i][j] += mem[i][j];
			}
		}
		return answer;
    }
}

---