문제
문제 해설
정상적으로 타일을 배치하려면 마지막에 반드시 ㅣ 혹은 = 가 들어와야 합니다.
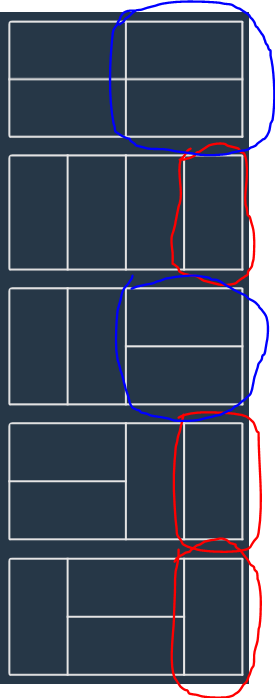
n = 4인 경우를 예시로 들면 다음과 같이 ㅣ 블럭으로 끝나면 빨간색, =블럭으로 끝나면 파란색으로 나누었습니다.
각 경우는 n=3인 모든 경우에 빨간 블럭을 더한 것 + n=2인 모든 경우에 파란 블럭을 더한 것의 총 개수이므로
A(n) = A(n-1) + A(n-2) 단, n >=3의 점화식을 세울 수 있습니다.
그리고 한 가지 유의할 점은 n이 커질 수록 저장되는 값이 매우 커지기 때문에 1000000007으로 나눈 값들을 저장해야 한다는 것입니다.
모듈러 연산의 특성상 원래 두 값을 더하고 나누어도, 나머지들을 더한 뒤 나누어도 같은 값을 가지기 때문입니다.
(a + b) mod n = ((a mod n) + (b mod n)) mod n
풀이 코드
def solution(n):
dp = [1] * (n + 1)
for i in range(2, n + 1):
dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007
return dp[i]
