문제
문제 해설
비트 연산을 이용해 현재 어떤 발전기를 켰는지 체크하고, 메모이제이션을 활용해 시간복잡도와 공간복잡도를 줄이며 푸는 문제입니다.
처음에 생각난 방식은 다음과 같습니다.
현재 켜져있는 발전기 중 가장 비용이 적게 드는 꺼져있는 발전기를 택한다.(그리디)
이 방식의 문제점은 답이 아닌 다른 반례가 존재한다는 것입니다.
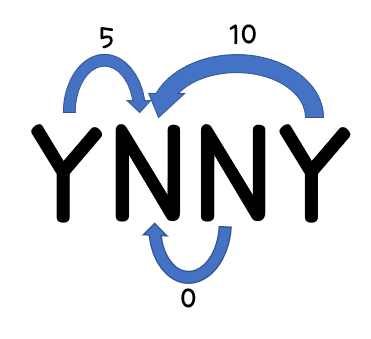
다음 그림과 같이 그리디하게 풀게 된다면 0번Y가 1번 N을 택하게 될것이고 당연히 답이 아니게 됩니다.그러므로, 다른 방법을 모색하되 현재 어떤 발전소가 켜져있는지를 알아야 한다는 사실을 인지해야 합니다.
다음 생각난 방식은 다음과 같습니다.
현재 켤 수 있는 발전소를 하나씩 P까지 킨다. (BFS)
이 방식은 큐를 사용하여 발전소의 정보를 큐에서 꺼낸 후 꺼져있는 발전소를 하나씩 켠 후 큐에 담는 방식입니다.
이 방식은 모든 경우의 수를 검사할 수 있지만, 문제점이 생깁니다.
N <= 16이기 때문에 최악의 경우 큐에 들어가는 개수가 점점 많아집니다.
> 15개, 14^2개, 13^3개, ...
그러므로 시간, 공간 복잡도가 모두 터져 이것을 줄여나가는 방식을 택해야 합니다.
발전소를 하나씩 P까지 키되, 메모이제이션 된 값보다 작으면 큐에 삽입하지 않는 방식 (메모이제이션, 비트마스크)
이 방식은 발전소의 켜진 상태를 저장할 공간을 비트 연산을 통해 1 << N개로 저장하면서 공간 복잡도를 줄이고, 만약 이미 메모이제이션된 값보다 작을 경우 큐에 넣지 않아 시간 복잡도를 줄인 방식입니다.
꺼져있는 발전기에 가장 적은 cost를 사용하는 발전소를 사용합니다.
- 큐에
string, cost를 넣습니다.- 큐에서 pop 한 뒤, 꺼져있는 발전기가 있는지 검사합니다. 있다면 그 발전기를 최소 비용으로 킵니다.
- 큐에 넣기전 그 비용이 최소인지 메모이제이션 리스트를 검사합니다.
- 켜져있는 발전기가 p가 될 때까지 반복합니다.
- 큐에는 현재 켜져있는 발전기가 p개인 경우만 담았으므로 모두 빼서 정답과 비교합니다.
주의점
0 <= P <= N 이므로 p가 0이거나 발전소가 p보다 같거나 많이 켜졌을시 0을 출력해야하고, 발전소가 하나도 안 켜졌을 땐 진행이 불가하기 때문에 -1을 출력합니다.
풀이 코드
import sys
from collections import deque
input = sys.stdin.readline
n = int(input())
graph = []
dp = [1000] * (1 << n) # 총 저장될 경우의 수가 1 << n
q = deque()
for _ in range(n):
graph.append(list(map(int, input().split())))
string = input().rstrip()
p = int(input())
time = now = 0
for i in range(len(string)):
if string[-i - 1] == "Y":
now += 2 ** i
time += 1
def solution():
global now, p, n, time
dp[now] = 0
answer = 1000
# p가 0이거나 발전소가 p보다 같거나 많이켜짐
if p == 0 or time >= p:
return 0
# 발전소가 하나도 안켜져서 진행이 불가함
elif time == 0:
return -1
else:
q.append((now, 0))
# 요구된 발전소를 모두 켤 때까지
while time < p:
size = len(q)
for _ in range(size):
now, cost = q.popleft()
for i in range(n):
# N이 보이면 일단 가장 작은 cost로 켜서 큐에 넣음
if (1 << i) & now == 0:
tmp = sys.maxsize
for j in range(n):
# 켜져있는 발전소 중 가장 cost 작은거
if (1 << j) & now == 1 << j:
tmp = min(tmp, graph[n - 1 - j][n - 1 - i])
# dp의 값과 비교 후 더 작으면 갱신 후 큐에 삽입
if dp[now + (1 << i)] > cost + tmp:
q.append((now + (1 << i), cost + tmp))
dp[now + (1 << i)] = cost + tmp
time += 1
# 큐에는 발전기가 p개 켜져있는 경우만 담겨있음.
while q:
_, cost = q.pop()
answer = min(answer, cost)
return answer
print(solution())