 ### 문제
### 문제
문제 해설
2차원 DP로 푸는 문제입니다. 각 DP에 객차를 넣을지 말지 판단하는 문제라 0-1 knapsack과 유사한 문제라고도 할 수 있겠습니다.
DP에는 기관차의 수, 객실번호를 인덱스로 최대 손님수를 저장합니다.
ex) DP[2][5] = 105 -> 기관차가 2대, 객실번호가 5번일때 최대 105명
total에는 객실 번호를 인덱스로 1번 부터 i번까지의 총 손님 수를 저장합니다.
ex) total[5] = 250 -> 1번부터 5번객실까지 총 손님 수
위와 같이 저장하는 이유는 DP를 채울 때마다 계산하기 번거로우므로 미리 저장된 리스트를 만들어 앞으로 사용될 계산을 범용성이 있게 저장해주는 겁니다.
점화식은 다음과 같습니다.
DP[N][M]=max(DP[N][M−1], DP[N−1][M−K]+S[M]−S[M−K])
기관차가 1개부터 3개, 객차 번호가 1번부터 n개까지 3*n의 2중 for문을 사용합니다.
DP를 채우는 과정은 점화식을 보면 바로 알 수 있는데 바로 전 객차까지 이용했을 때 VS 현 객차를 이용할시 손님 수 + 객차 하나 뺐을 때 DP 값입니다.
그림으로 설명드리자면
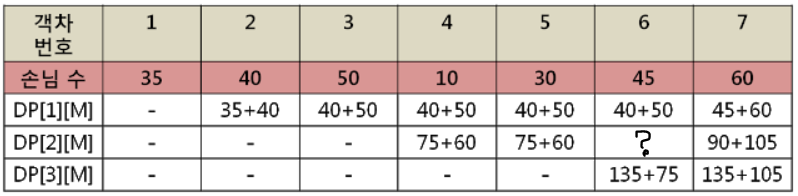
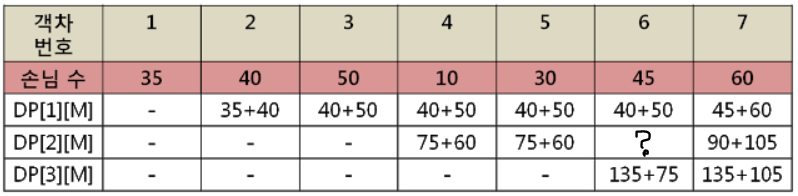
다음의 물음표를 채워 보겠습니다.
DP[2][6](기관차 2개를 이용해 6번객차까지의 최대 손님 수)를 구하는게 목표입니다.
일단 현 객차를 이용할때의 손님 수는 total[6]-total[4] = 75명 입니다.
현 객차를 이용했을때 2칸을 차지하니 DP[1][4]로 가서 값을 확인합니다. 기관차 하나가 4번객차까지 최대 90명을 태울 수 있습니다.
마지막으로 1~4번까지 최대 승객을 태운 기관차와 5~6번 승객을 태운 현 객차를 합친 것(75 + 90)과 1~5번 까지 총 2대의 기관차가 최대 승객을 태운 수(75 + 60)를 비교하여 큰 값을 저장하면 마지막 DP에는 우리가 원하는 답을 구할 수 있습니다!
풀이 코드
import sys
input = sys.stdin.readline
n = int(input())
car = list(map(int, input().split()))
car.insert(0, 0)
carry = int(input())
# dp에는 기관차 수와 객차 번호에 해당하는 인덱스에 최대 손님 수 저장
# dp[N][M] = 100, 기관차 N개를 써서 M번 번호 객차까지 최대 손님수가 100명
dp = [[0] * (n + 1) for _ in range(4)]
# total에는 1번객차부터 n번까지 총 인원수가 들어있다.
# 기관차가 최대 2개 이상의 객차를 끌 수도 있으므로 계산편의상 이렇게 하는게 편하다.
total = [0]
for i in range(1, n + 1):
total.append(total[i - 1] + car[i])
for i in range(1, 4):
for j in range(carry, n + 1):
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j - carry] + total[j] - total[j - carry])
print(dp[3][n])