백준 1647번: 도시 분할 계획

문제 설명

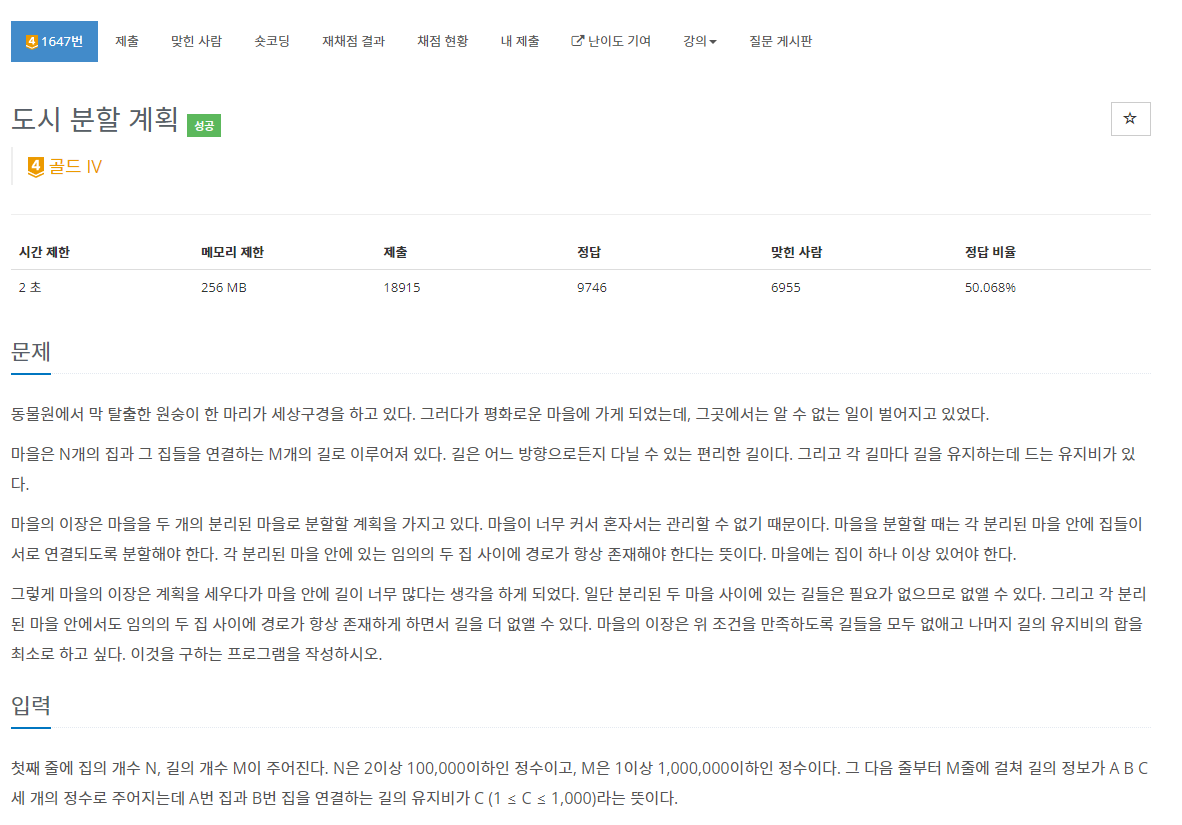
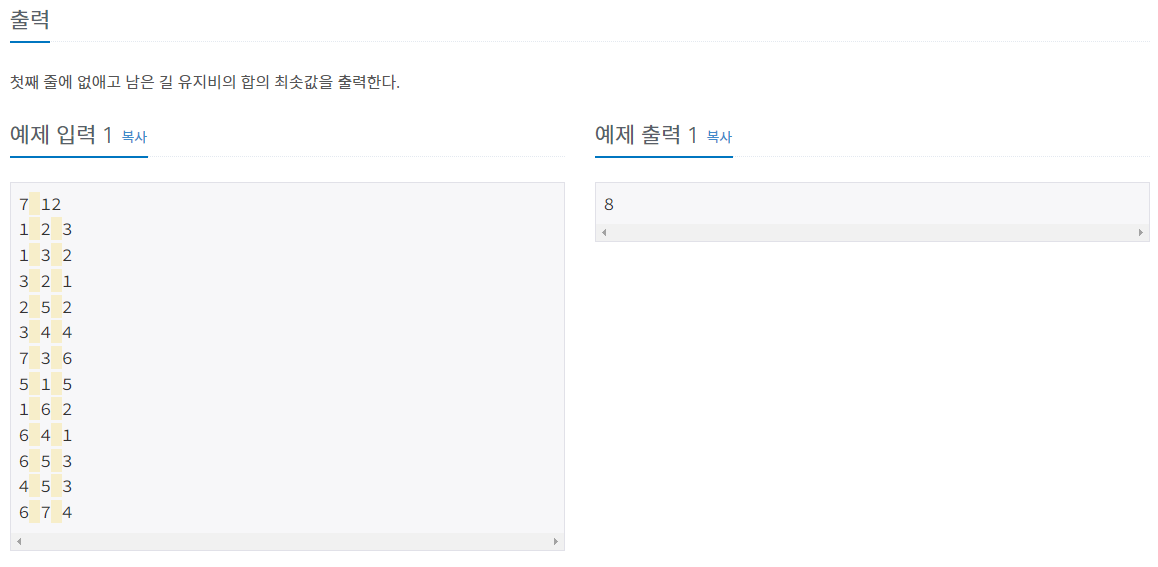
• https://www.acmicpc.net/problem/1647
• 최소 비용으로 그래프를 두개의 집단으로 나눠야 합니다.
  하나의 집단에서는 임의의 두 점 a,b에 대해 a에서 b로 이동하는 경로가 존재해야 합니다.

접근법

• 모든 노드를 최소비용으로 연결하는 최소 스패닝 트리를 사용한 뒤 여기서 연결비용이 가장 큰 간선을 하나 지우면 최소비용으로 두 개의 집단을 만들 수 있습니다.
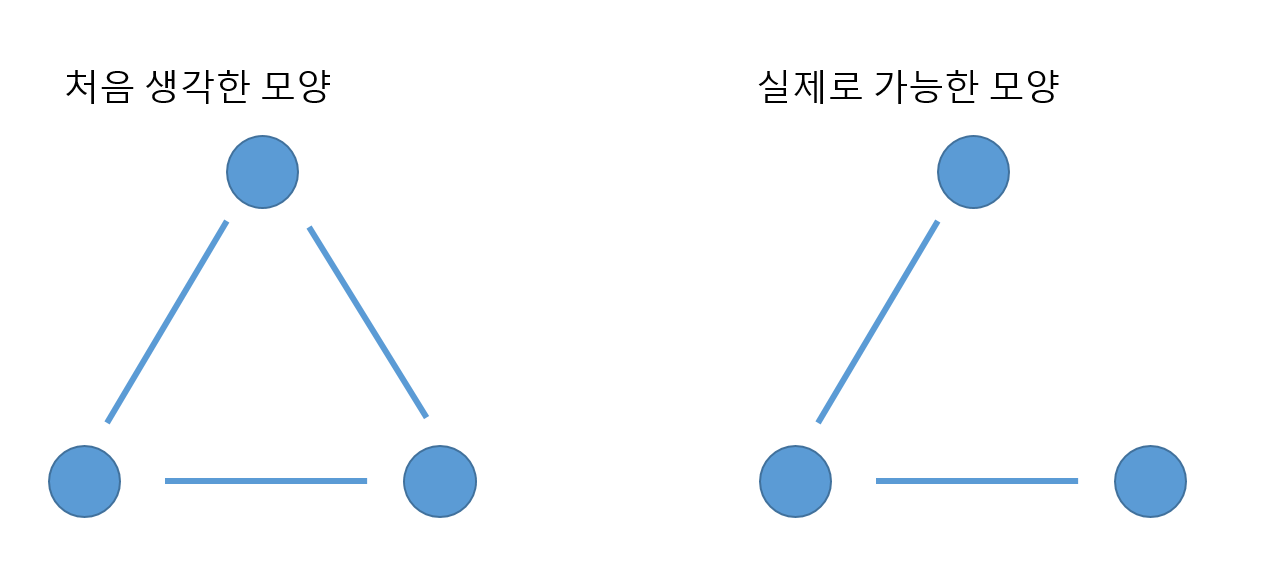
• 문제에서 각 분리된 마을 안에 있는 임의의 두 집 사이에 '경로'가 항상 존재해야 한다를 처음에 잘못 이해했었습니다.
  마을 안에 있는 두 집 사이를 직접 연결하는 간선이 존재해야되는줄 알았는데 그게 아니라 어떻게든 a에서 b로 이동할 수만 있으면 되는거였습니다.
  

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int[] parent = new int[N+1];
		for (int i = 0; i <= N; i++) {
			parent[i] = i;
		}
		PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a,b)->a[2]-b[2]);
		for (int i = 0; i < M; i++) {
			st = new StringTokenizer(br.readLine());
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			int c = Integer.parseInt(st.nextToken());
			pq.add(new int[] {a,b,c});
		}
		int answer = 0;
		int lastEdge = 0; // 모든 마을을 하나로 연결했을 때 가장 비용이 큰 간선 -> 해당 간선을 지움으로써 마을이 2개로 나뉨
		while(!pq.isEmpty()) {
			int[] now = pq.poll();
			int a = now[0];
			int b = now[1];
			int c = now[2];
			if(findParent(a,parent) != findParent(b,parent)) {
				union(a,b,parent);
				answer += c;
				lastEdge = c;
			}			
		}
		System.out.println(answer-lastEdge);
	}
	
	public static int findParent(int x, int[] parent) {
		if(parent[x] == x) return x;
		parent[x] = findParent(parent[x],parent);
		return parent[x];
	}
	
	public static void union(int a, int b, int[] parent) {
		int pa = findParent(a,parent);
		int pb = findParent(b,parent);
		if(pa>pb) {
			parent[pa] = pb;
		}else {
			parent[pb] = pa;
		}
		
	}
}