백준 11054번: 가장 긴 바이토닉 부분 수열

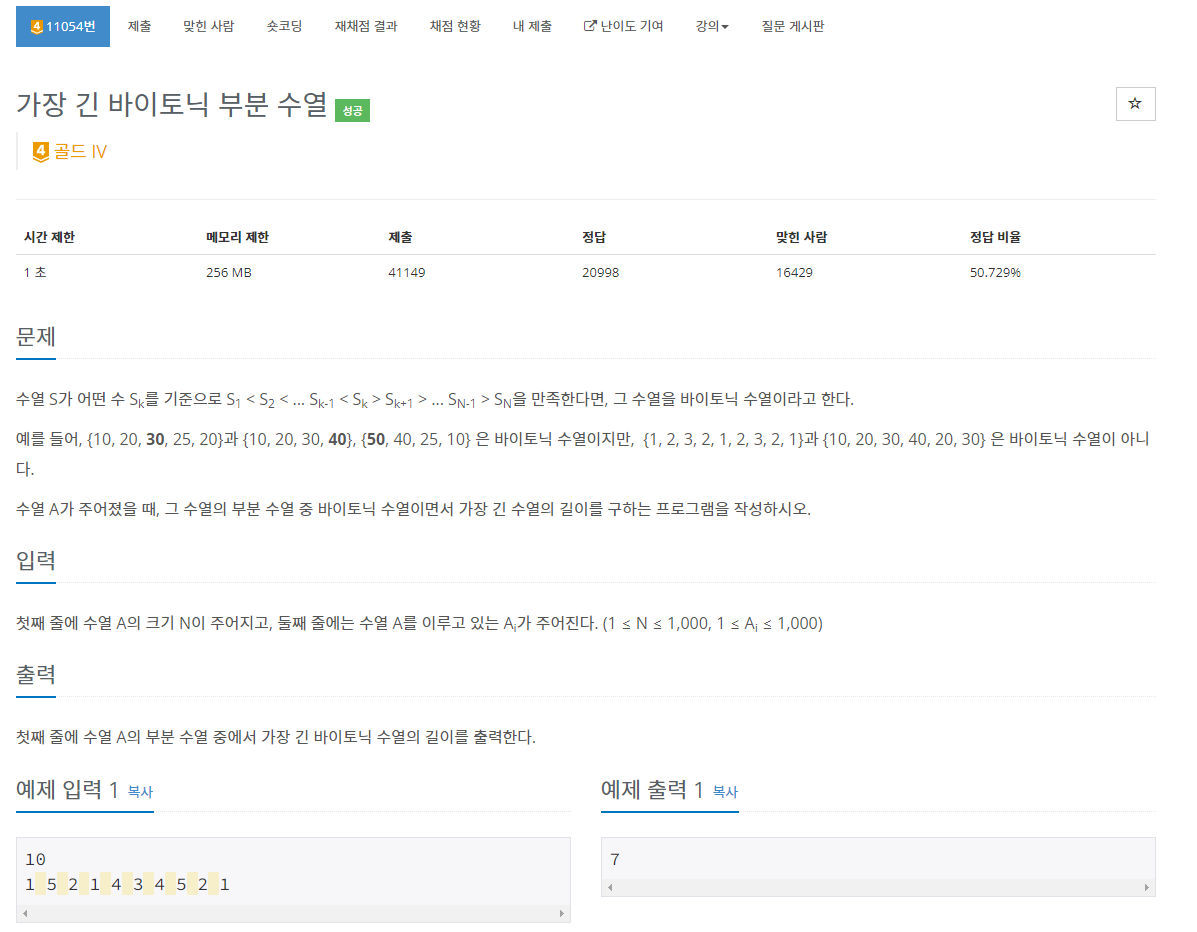
문제 설명

• https://www.acmicpc.net/problem/11054
• 증가했다가 감소하는 수열 or 증가하는 수열 or 감소하는 수열 중 가장 긴 수열의 길이를 구하는 문제입니다.

접근법

• 앞에서부터 증가하는 수열의 길이와 뒤에서부터 증가하는(감소하는) 수열의 길이를 구합니다. 꺽어지는 위치를 i라고 했을 때 '두 수열의 합 -1'을 해 주면 그게 바로 i가 꺽어지는 지점일 때 최장 바이토닉 부분 수열의 길이입니다.
  • -1을 해주는 이우는 증가하는 수열과 감소하는 수열 모두에서 i번째 값이 포함되었기 때문에(중복) 하나를 제거해 줍니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		StringTokenizer st = new StringTokenizer(br.readLine());
		int[] arr = new int[N];
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken()); 
		}
		int[] ascendingDp = new int[N];
		Arrays.fill(ascendingDp, 1);
		for (int i = 1; i < N; i++) {
			for (int j = 0; j < i; j++) {
				if(arr[j] < arr[i]) {
					ascendingDp[i] = Math.max(ascendingDp[i], ascendingDp[j]+1);
				}
			}
		}
		int[] descendingDp = new int[N];
		Arrays.fill(descendingDp, 1);
		for (int i = N-2; i >= 0; i--) {
			for (int j = N-1; j > i; j--) {
				if(arr[j] < arr[i]) {
					descendingDp[i] = Math.max(descendingDp[i], descendingDp[j]+1);
				}
			}
		}
		
//		System.out.println(Arrays.toString(ascendingDp));
//		System.out.println(Arrays.toString(descendingDp));
		int answer = 0;
		for (int i = 0; i < N; i++) {
			answer = Math.max(answer, ascendingDp[i]+descendingDp[i]-1);
		}
		System.out.println(answer);
	}

}