DFS와 BFS

최창효·2022년 1월 22일

완전탐색

무언가를 찾는 탐색에서 가능한 모든 경우의 수를 모두 확인하는 방법이 바로 완전탐색입니다.
윌리를 찾아 봅시다. 우리는 다음과 같이 다양한 방법으로 윌리를 찾으려 할 것입니다.

이처럼 '어떤 방식으로 모든 수를 확인할 것인가?'에 대한 물음에 우리는 BFS 혹은 DFS를 답할 수 있습니다. 즉 BFS와 DFS는 가등한 모든 경우의 수를 확인하는 방법의 종류라는 뜻입니다.

DFS와 BFS

DFS와 BFS는 각각 Depth_First_Search(깊이_우선_탐색)과 Breadth_First_Search(너비_우선_탐색)의 함축어입니다.
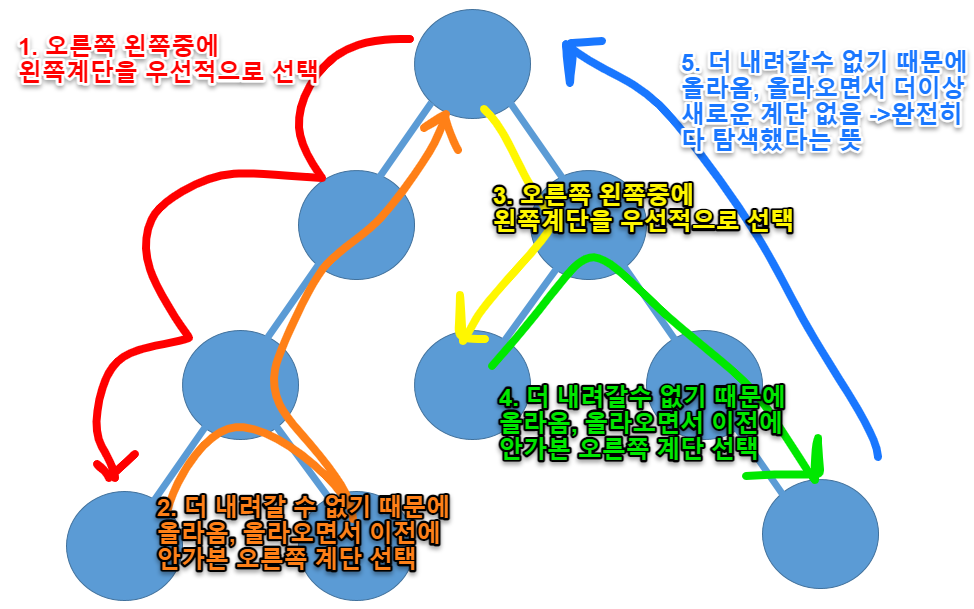
깊이 우선 탐색은 간단히 말해 다음과 같이 행동하는 것입니다.
- 두 개의 길 중에 좌측계단을 우선적으로 선택합니다.
  - 우측을 우선시해도 상관없습니다.
- 더 이상 내려갈 수 없으면 거슬러 올라가면서 선택하지 않았던 계단(오른쪽)을 선택합니다.

선택한 길에서 내려갈 수 있는 최대한의 깊이까지 내려갔다가, 다른 곳을 찾기 때문에 깊이 우선 탐색이라고 불립니다.
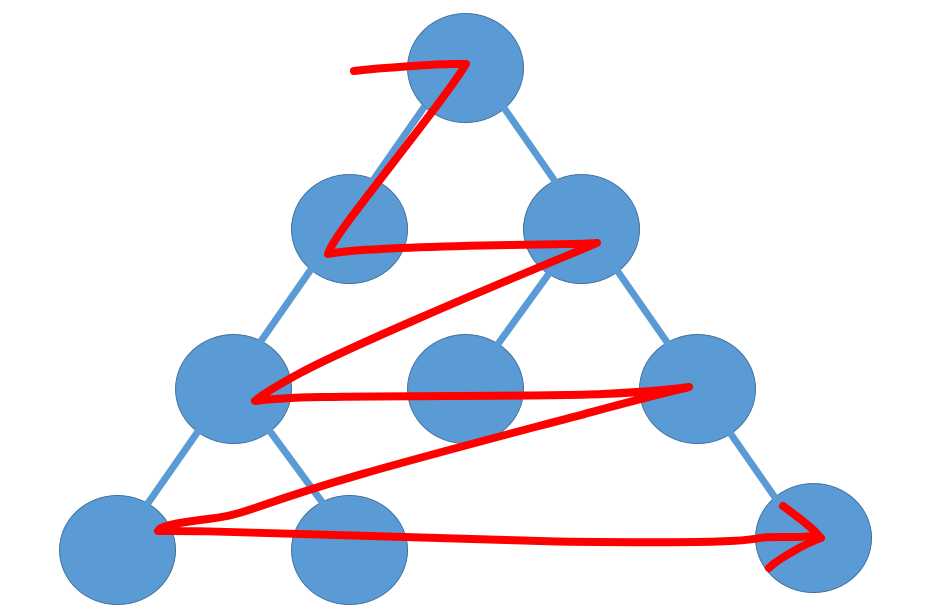
너비 우선 탐색은 위에 있는것들부터 먼저 확인하는 방식입니다.

구현

BFS는 `queue`를 통해, DFS는 `stack`을 통해 구현할 수 있습니다.

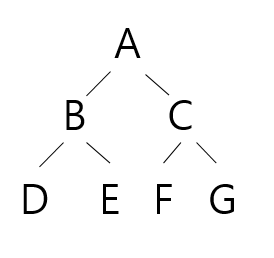
아래와 같은 트리가 있다고 생각해 봅시다.
BFS는 너비우선이기 때문에 A,B,C,D,E,F,G순서가 되어야 합니다. 그런데 A는 D,E,F,G의 정보를 알고 있을까요? A는 자식의 정보만 알고 있을 뿐 그 밑의 정보는 알지 못합니다. 그렇기 때문에 B와C를 방문했을 때 D,E,F,G에 대한 정보를 기억해 둬야 합니다.
- B로부터 나온 D와E를 C로부터 나온 F와G보다 먼저 얻기를 원하기 때문에 선입선출 관계가 됩니다.
- D,E,F,G중에서도 우리는 D와E의 정보를 먼저 얻기를 원합니다. D와E의 정보는 B로부터 나옵니다. 즉 B,C중 먼저 탐색한 B의 자식도 먼저 나와야 하기 때문에 선입선출의 관계가 성립합니다. (선입선출은 곧 큐 구조를 의미합니다.)
- 다음과 같이 비유할 수 있습니다. - BFS는 새롭게 약속을 잡을때 "이전에 있던 약속만 다 끝내고 니 약속도 들어줄께" 라고 얘기하는 친구입니다.
  - A는 B와 C를 방문할 일정을 가지고 있었습니다.
  - B를 방문해보니 D와E를 추가적으로 방문해야 한다는 사실을 깨달았습니다.
    - 이때 B에서 바로 D와E를 방문하지 않고 미리 계획해둔 C방문을 마친 뒤 D와E를 방문하기로 합니다.
  - 그래서 C를 방문해보니 F와G를 추가적으로 방문해야 한다는 사실을 깨달았습니다.
    - 이때도 앞에서 했던 규칙대로 이전 일정을 모두 소화하고 추가방문을 할 것이기 때문에 D와E 다음에 F와G가 옵니다.
    - 최종 방문순서가 A->B->C->D->E->F->G가 됩니다.
DFS는 일단 한방향으로 직진하고, 더이상 직진할 수 없을때 처음이 아니라 가장 최근 갈림길로 돌아가야 하기 때문에 후입선출의 관계가 성립합니다. (후입선출은 곧 스택 구조를 의미합니다.)

코드

#BFS
from collections import deque
def BFS(graph, start):
    queue = deque([])
    visited = [False]*len(graph)
    queue.append(start)
    visited[start-1] = True
    while queue:
        x = queue.popleft()
        print(x)
        for i in graph[x]:
            if not visited[i-1]:
                queue.append(i)
                visited[i-1] = True

#DFS
def DFS(graph,start):
    stack = []
    visited = [False]*len(graph)
    stack.append(start)
    visited[start-1] = True
    while stack:
        x = stack.pop()
        print(x)
        for i in graph[x]:
            if not visited[i-1]:
                stack.append(i)
                visited[i-1] = True