백준 12865번: 평범한 배낭

DP를 복습하기 위해 이전에 풀었던 배낭 문제를 다시 풀어봤습니다.
이전에는 1차원 배열을 활용해 풀었더군요. 이번에는 2차원 배열을 이용한 정석(?)적인 풀이입니다.

문제 설명

• N개의 물품을 용량 K인 배낭에 넣습니다.
• 물건은 각각 무게와 가치를 지니고 있으며, 우리는 배낭 속 물품의 가치가 최대가 되도록 물건을 넣어야 합니다.
• 물건은 1개만 존재하며 물건을 잘라서 넣는건 불가능합니다.

접근법

$DP[i][j] = Max(DP[i-1][j], DP[i-1][j-Wi] + Vi)$

• 배낭의 잔여 무게가 0~K일때 물건 i까지의 최적값을 고려해야 합니다.
  • 만약 board[i][K]의 값이 12라면 우리는 잔여무게가 K인 상황에서 물건1,물건2,...물건i로 만들 수 있는 최적값이 12라는 의미입니다.
  • 물건 i를 고려한다는 것과 물건 i를 배낭에 넣는다는 것은 다른 행위입니다.
• i번째 물건을 다음과 같은 두 가지 상황으로 고려할 수 있습니다. (전체 배낭의 용량을 K,i번째 물건의 무게가 Wi, 가치가 Vi일 때)
  • 첫째. i번째 물건을 넣지 않는다.
    • 이 경우 K,Wi,Vi는 i번째 물건을 고려하기 전과 동일합니다.
    • board[i][j] = board[i-1][j] 입니다.
  • 둘째. i번째 물건을 넣는다.
    • 이 경우 배낭의 잔여무게는 Wi만큼 줄어들고 배낭속 가치는 Vi만큼 증가합니다.
      • 만약 잔여 무게가 j인 배낭에 i물건을 넣었다면 앞으로 j-Wi만큼의 잔여무게를 더 채울 수 있습니다.
      • i를 이미 넣었기 때문에 j-Wi의 잔여무게를 채울 때에는 i물건을 뺀 1~i-1까지의 물건으로만 구성해야 합니다. (물건은 1개만 존재한다는 조건)
      • 1~i-1까지의 물건으로 j-Wi무게를 최적으로 채우는 방법은 board[i-1][j-Wi]입니다.
    • 이를 종합하면 i번째 물건을 넣었을 때 최적값은 다음과 같습니다.
      • board[i][j] = board[i-1][j-Wi] + Vi
  • 우리는 i번째 물건을 넣는 첫번째 경우와 i번째 물건을 넣지 않는 두번째 경우 중 더 큰 값을 선택합니다.
    • board[i][j] = Max(board[i-1][j], board[i-1][j-Wi]+Vi)
• 그림으로 표현하면 다음과 같습니다.

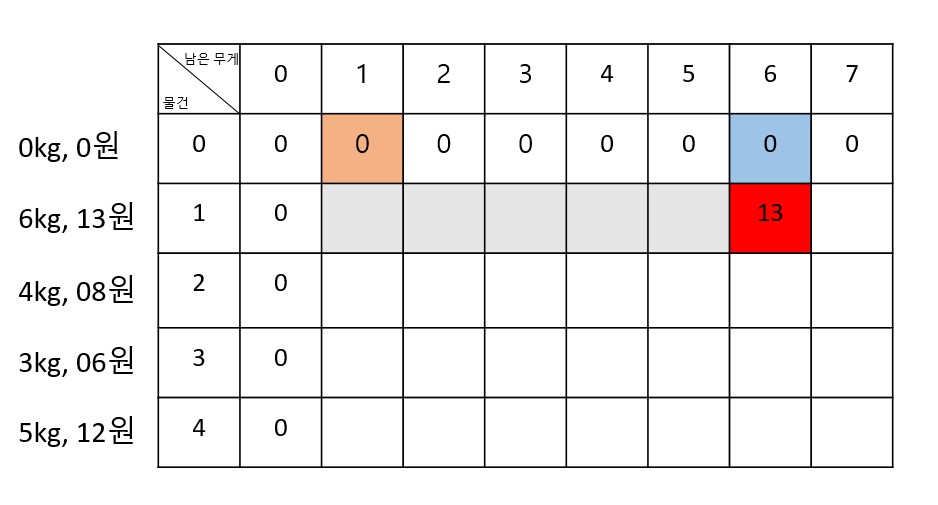
• board[1][6] = Max(board[0][6],board[0][0]+13)

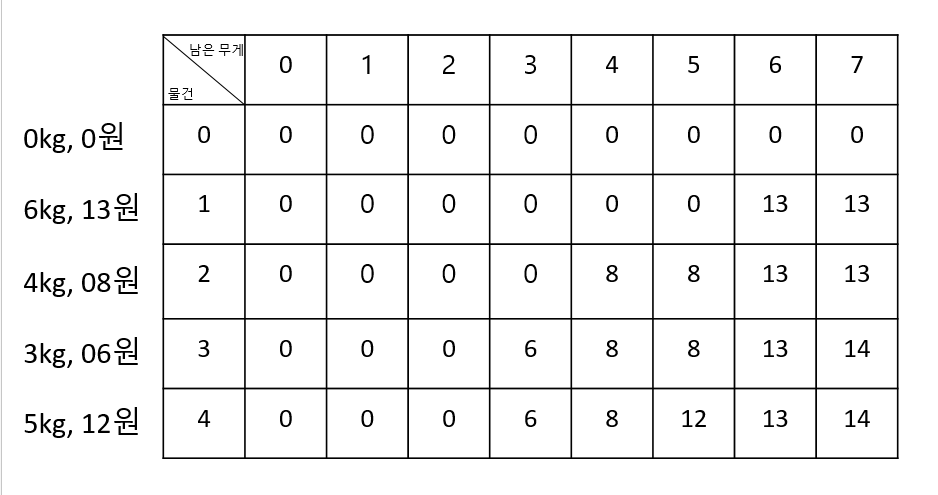
pseudocode

for (i는 1부터 n까지)
	for( w는 1부터 W까지)
    	if(wi > W){
        	board[i][w] = board[i-1][w]
        }else{
        	board[i][w] = max(vi+board[i-1][W-wi], board[i-1][w])
        }

정답

import java.util.*;

class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int K = sc.nextInt();
		List<Obj> lst = new ArrayList<Obj>();
		int[][] board = new int[N + 1][K + 1];
		for (int i = 0; i < N; i++) {
			int W = sc.nextInt();
			int V = sc.nextInt();
			lst.add(new Obj(W, V));
		}
		for (int i = 1; i <= N; i++) { // i번째 물건
			for (int j = 1; j <= K; j++) { // 배낭의 무게가 j일때
				Obj obj = lst.get(i - 1);
				if (obj.W > j) { // j물건을 담을 수 없는 경우
					board[i][j] = board[i - 1][j];
				} else {
					board[i][j] = Math.max(board[i - 1][j], obj.V + board[i - 1][j - obj.W]);
				}
			}
		}

		System.out.println(board[N][K]);

	}

	static class Obj {
		int W;
		int V;

		public Obj(int w, int v) {
			super();
			W = w;
			V = v;
		}

		@Override
		public String toString() {
			return "Obj [W=" + W + ", V=" + V + "]";
		}

	}
}

기타

• 해당 문제는 다양한 방식으로 최적화가 가능합니다.
  • 2차원 배열에서 board[i][]의 값을 구할 때 우리는 board[i-1][]의 값만 활용합니다.
    즉 직전값만 있으면 현재의 값을 갱신할 수 있기 때문에 2차원 배열의 행을 2개(직전행,현재행)만 사용할 수 있습니다.
  • 2차원배열이 아닌 1차원 배열에 정보를 담는 것도 가능합니다.
    • board[i]=여분의 무게가 i일 때 모든 물건을 고려한 최적의 가치 입니다.
    • 유의할 점은 1차원 배열로 문제를 풀 때에는 뒤에서부터 값을 채워야 합니다.
    • 1차원 배열로 풀면서 앞에서부터 값을 채우는 건 물건의 개수가 무한하다는것과 같은 의미입니다.

여분의 무게가 4kg일 때 우리는 2kg짜리 물건 1을 선택하고(A), 남은 2kg을 최적의 가치로 채워야 합니다(B).
A과정에서 물건1을 사용했기 때문에 B과정을 진행할 때 2kg의 최적의 가치는 0이 되어야 합니다.
1차원 배열에서는 이러한 내용이 고려되지 못하고 2kg물건이 여러개인 것처럼 14로 업데이트 됩니다.

뒤에서부터 채울 경우 board[i-w]가 아직 갱신되지 않은 상태이기 때문에 올바르게 가치를 고려할 수 있습니다.