백준 13398번: 연속합 2

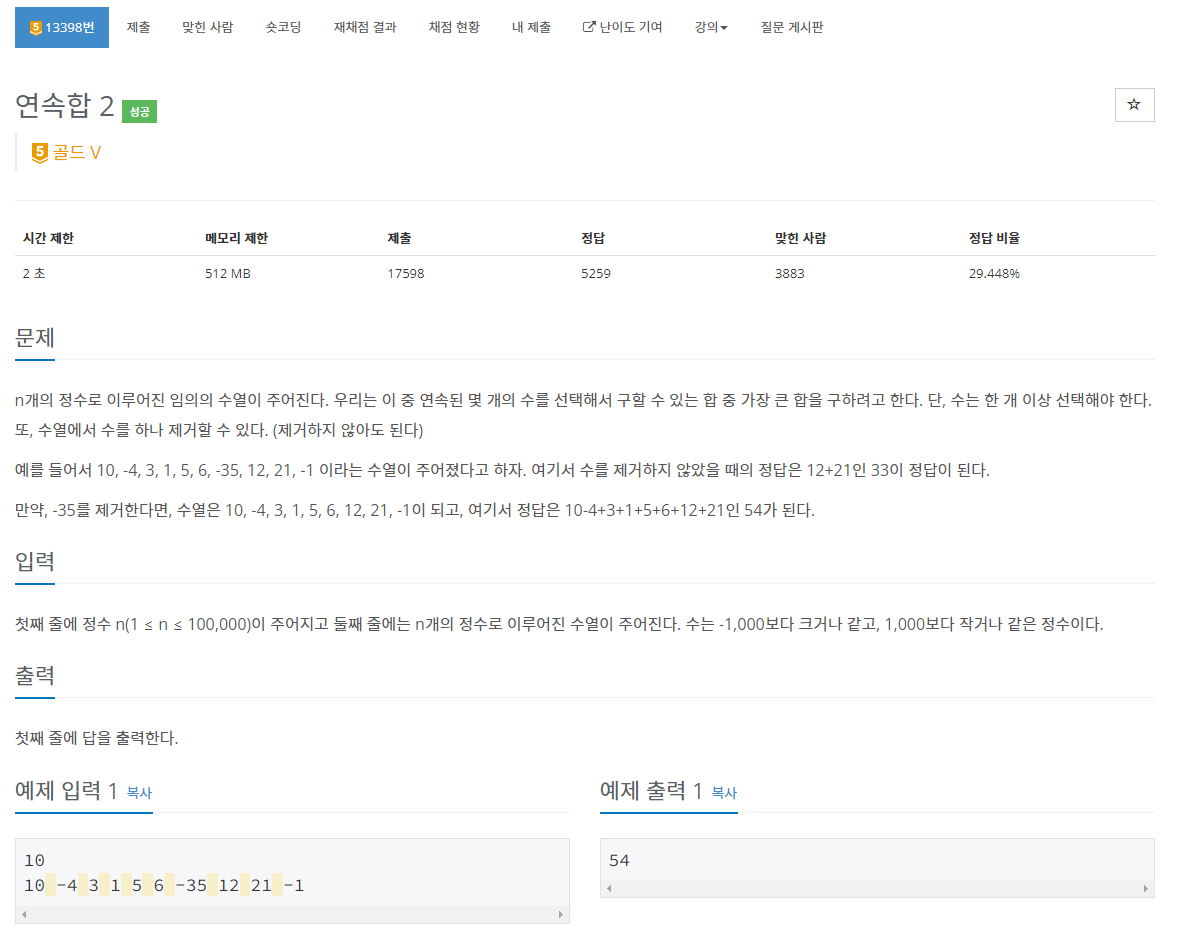
문제 설명

• https://www.acmicpc.net/problem/13398
• 연속된 구간합 중 가장 큰 합을 구하는 문제입니다.
  이때 N개의 정수 중 최대 하나의 숫자를 제거할 수 있습니다.

접근법

• 문제가 어려우신 분들은 1912번: 연속합을 먼저 풀어보시는 걸 추천합니다.
• 처음에는 제거되는 숫자를 특정할려고 했습니다. 그 결과 O(N^2)의 풀이가 되어버려 다른 방식을 고민했습니다.
• 행이 제거한 숫자의 개수를 의미하는 2차원 배열로 문제를 해결할 수 있습니다.
  dp[0][i] = 숫자를 총 0개 제거함. i번째 숫자까지 고려했을 때 가장 큰 구간합
  dp[1][i] = 숫자를 총 1개 제거함. i번째 숫자까지 고려했을 때 가장 큰 구간합
  • dp[0][i] = dp[0][i-1]에 i번째를 더하거나, 앞의 값을 포기하고 i번째 값만 가지거나
  • dp[1][i] = dp[0][i-1]에서 i번째를 선택하지 않거나, dp[1][i-1]에서 i번째를 선택하거나, 앞의 값을 포기하고 i번째 값만 가지거나

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		StringTokenizer st = new StringTokenizer(br.readLine());
		int[] arr = new int[N];
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		int[][] dp = new int[2][N];
		dp[0][0] = arr[0];
		
		int answer = dp[0][0];
		for (int i = 1; i < N; i++) {
			dp[0][i] = Math.max(dp[0][i-1]+arr[i], arr[i]);
			dp[1][i] = Math.max(dp[0][i-1], Math.max(dp[1][i-1]+arr[i], arr[i]));
			answer = Math.max(Math.max(answer, dp[0][i]),dp[1][i]);
		}
		System.out.println(answer);
		
//		for (int i = 0; i < 2; i++) {
//			System.out.println(Arrays.toString(dp[i]));
//		}
		
	}
}