백준 20152번: Game Addiction

문제 설명

• https://www.acmicpc.net/problem/20152
• 2차원 좌표평면 위 (H,H)에서 (N,N)으로 이동할 수 있는 경우의 수를 구하는 문제입니다.
  단, y>x인 좌표로는 이동할 수 없습니다.

접근법

• 좌표의 위치는 중요하지 않고 거리가 중요합니다. (1,1)에서 (3,3)으로 가는 것과 (2,2)에서 (4,4)으로 가는 경우의 수는 동일합니다. 또한 집과 PC방의 좌표는 항상 y=x위에 존재합니다.
• 어떤 좌표 (x,y)로 가는 경우의 수는 (x-1,y)까지의 경우의 수 + (x,y-1)까지의 경우의 수 입니다.
  
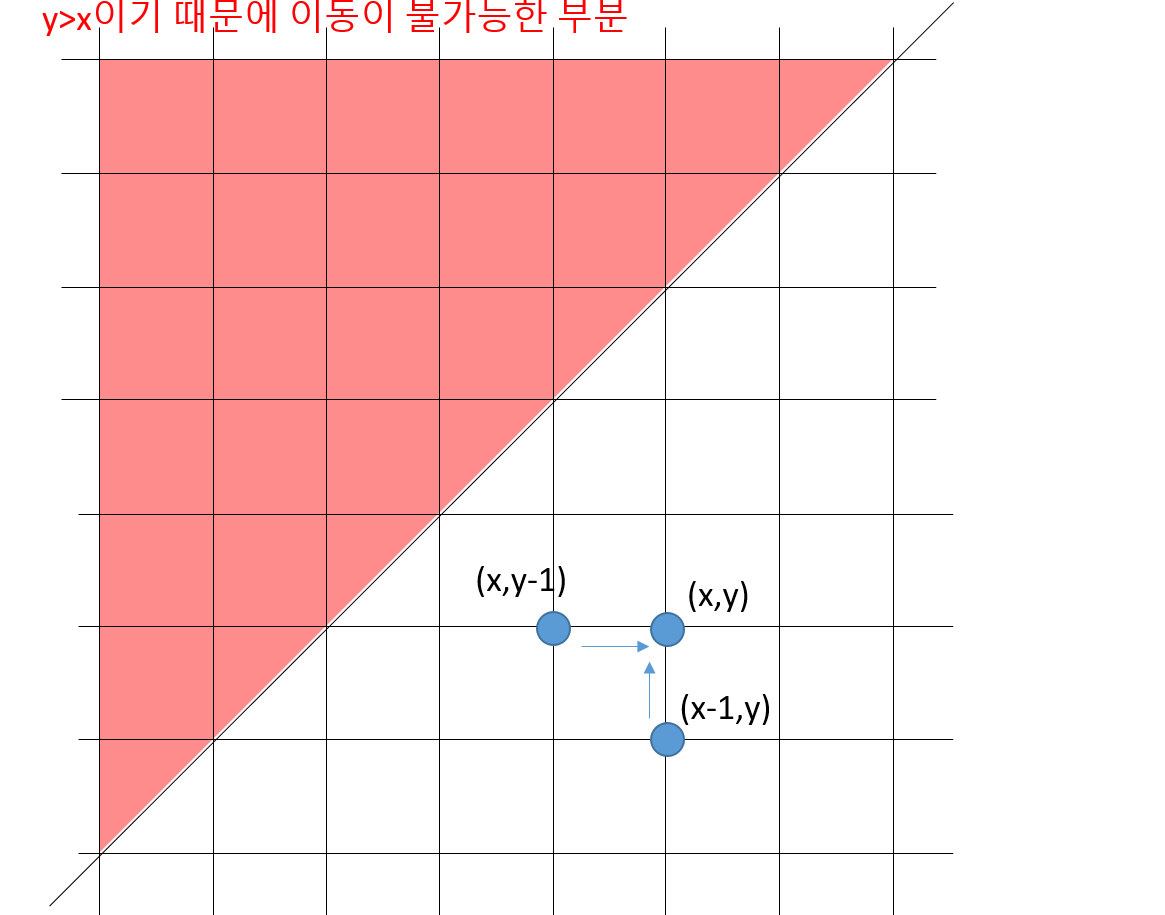
• 이를 기준으로 예제인 (8,8)과 (4,4)를 계산해 보면 다음과 같습니다.(편의상 (4,4)에서 (8,8)로의 이동을 계산했습니다.)
  좌표에 표시된 숫자는 해당 경로까지 이동할 수 있는 경우의 수 입니다.
  ![](https://velog.velcdn.com/images/qwerty1434/post/dbf9df46-f723-467f-beb5-573eb0edd76c/image.png
  
  

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception{
		Scanner sc = new Scanner(System.in);
		int H = sc.nextInt();
		int N = sc.nextInt();
		int D = Math.abs(N-H);
		long[][] dp = new long[D+1][D+1];
		Arrays.fill(dp[0], 1);
		
		for (int i = 1; i <= D; i++) {
			dp[i][i] = dp[i-1][i];
			for (int j = i+1; j <= D; j++) {
				dp[i][j] = dp[i][j-1]+dp[i-1][j];
			}
		}
//		for (int i = 0; i < dp.length; i++) {
//			System.out.println(Arrays.toString(dp[i]));
//		}
		System.out.println(dp[D][D]);

	}
	
}