백준 13398번: 연속합 2

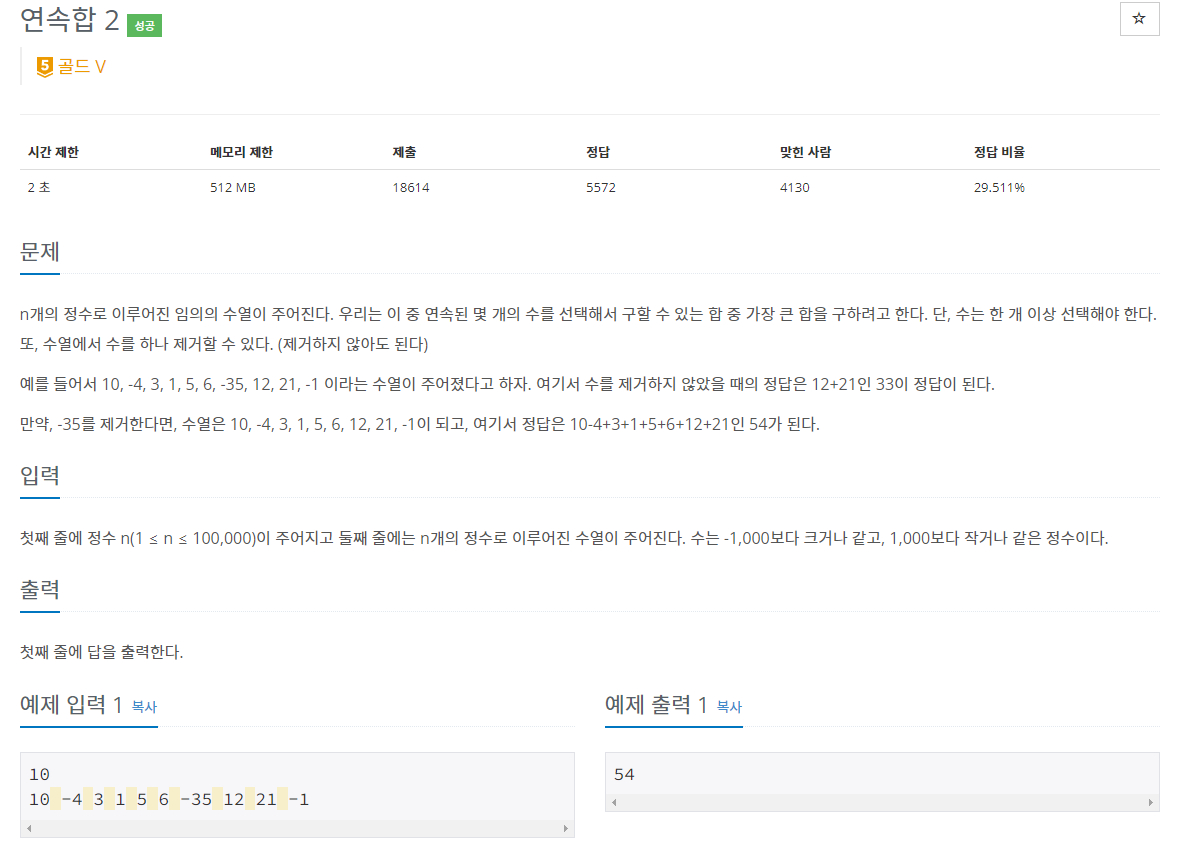
문제 설명

• https://www.acmicpc.net/problem/13398
• 구간의 누적합들 중 가장 큰 값을 구하는 문제입니다.
  최대 1번 원소를 누적합에 반영시키지 않을 수 있습니다.

접근법

• 수를 제거한 경우를 고려하기 위해 dp[2][N]을 설계합니다.
  dp[0][i]는 수를 하나 제거하지 않으면서 i번째까지 고려했을때의 최댓값입니다.
  dp[1][i]는 수를 하나 제거해서 얻은 i번째까지 고려했을때의 최댓값입니다.

• dp[0][i]는 앞선 누적값을 이어나갈 것이냐, 아니면 리셋하고 지금부터 누적을 시작할 것이냐를 고민하면 됩니다.

  • dp[0][i] = Math.max(dp[0][i-1] + arr[i],arr[i]);
    • dp[0][i-1] + arr[i]: 앞선 누적값을 이어나감
    • arr[i]: 새롭게 누적 시작
  • 이거 자체를 문제로 출제하기도 합니다: 4097 수익, 1912 연속합

• dp[1][i]는 이미 한 번의 기회를 사용한 상태에서 값을 더할지, 아니면 이번에 한 번의 기회를 사용할지를 고민하면 됩니다.

  • dp[1][i] = Math.max(dp[1][i-1] + arr[i], dp[0][i-1]);
    • dp[1][i-1] + arr[i]: 이미 한 번의 기회를 사용한 상태
    • dp[0][i-1]: 이번에 기회를 사용

• n번째 값이 항상 최적값이 아닐 수 있습니다. answer변수를 사용해 중간에 만들어진 값을 비교해 최적값을 항상 갱신시켜 줍니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];
		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		int[][] dp = new int[2][N];
		dp[0][0] = arr[0];
		int answer = arr[0]; // 수를 하나 반드시 선택해야 함
		for (int i = 1; i < N; i++) {
			dp[0][i] = Math.max(dp[0][i-1] + arr[i],arr[i]);
			dp[1][i] = Math.max(dp[1][i-1] + arr[i], dp[0][i-1]);
			answer = Math.max(answer, Math.max(dp[0][i], dp[1][i]));
		}
		System.out.println(answer);
	}
}