백준 2156번: 포도주 시식

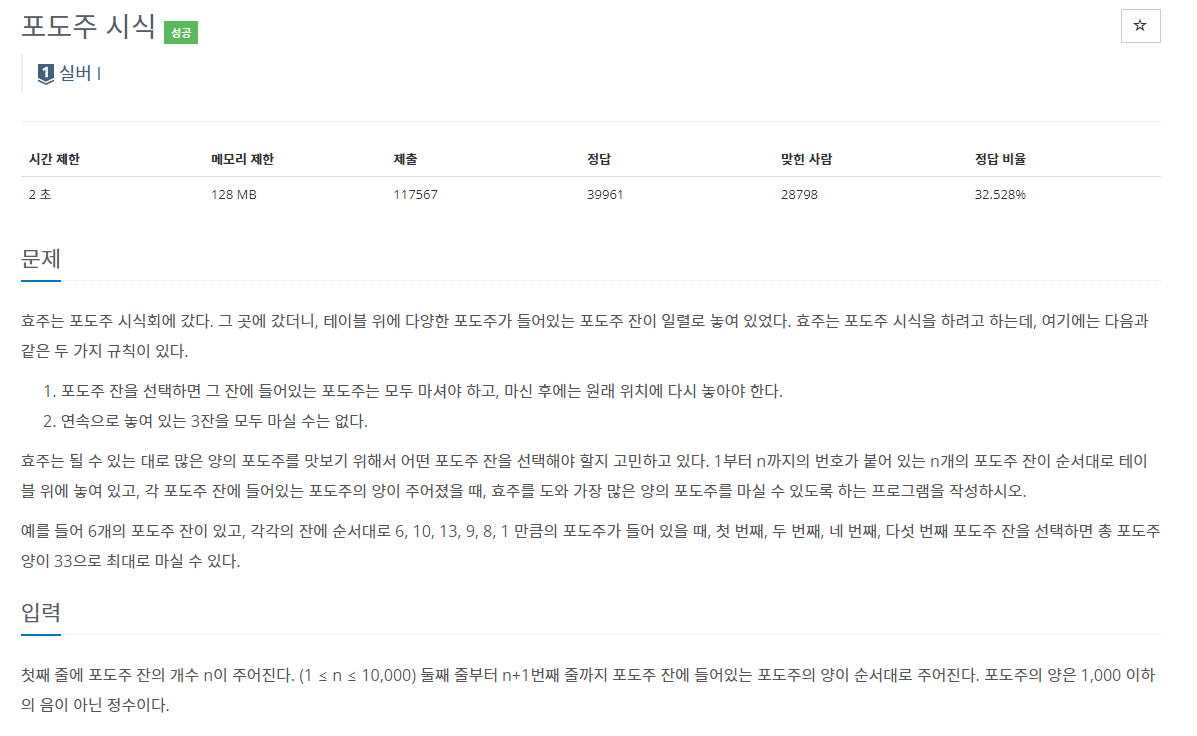
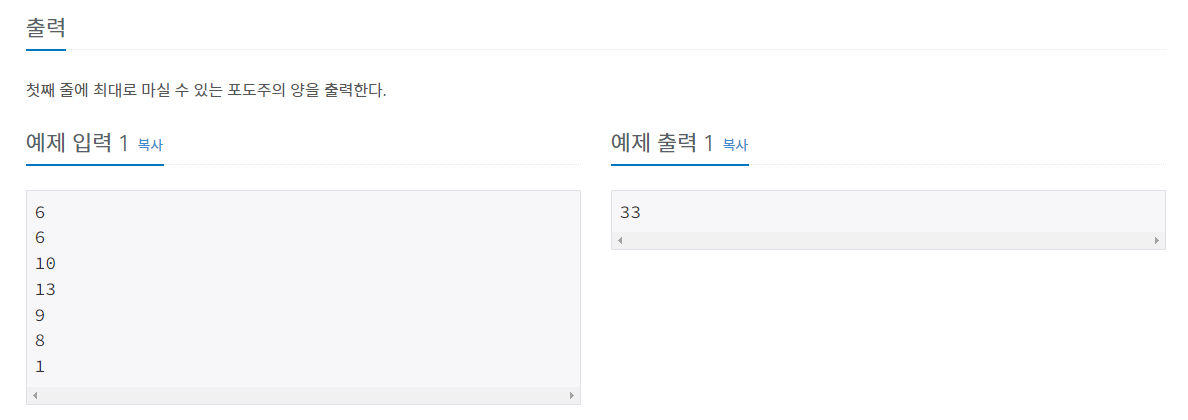
문제 설명

• https://www.acmicpc.net/problem/2156
• 연속해서 3개를 선택할 수 없습니다.
  선택할 수 있는 최댓값을 구하는 문제입니다.

접근법

• 행을 연속된 잔의 수로 두는 2차원 dp배열을 이용했습니다.
  dp[c][i]는 i까지 고려했을 때 마신 최댓값, 현재까지의 연속된 잔은 c개입니다.
  • dp[0][i]: i번째 잔까지 고려했을 때 연속된 잔이 0개이려면 i번째를 마시지 않아야 합니다.
  • dp[1][i]: i번째 잔까지 고려했을 때 연속된 잔이 1개이려면 i-1번째를 마시지 않고, i번째를 마셔야 합니다.
  • dp[2][i]: i번째 잔까지 고려했을 때 연속된 잔이 2개이려면 i-1번째에 한잔을 마시고, i번째도 마셔야 합니다.
• 연속된 잔의 수가 0이라는 0번 행을 표시했을 때 훨씬 쉽게 풀 수 있었습니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[Math.max(2,N)];
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		
		int[][] dp = new int[3][N];
		dp[1][0] = arr[0];
		for (int i = 1; i < N; i++) {
			dp[0][i] = Math.max(Math.max(dp[0][i-1], dp[1][i-1]),dp[2][i-1]);
			dp[1][i] = dp[0][i-1] + arr[i];
			dp[2][i] = dp[1][i-1] + arr[i];
		}
		int answer = Math.max(Math.max(dp[0][N-1], dp[1][N-1]),dp[2][N-1]);
		System.out.println(answer);
	}
}