백준 16974번: 레벨 햄버거

문제 설명

• https://www.acmicpc.net/problem/16974
• 레벨-N 버거에서 아래 X장을 먹었을 때 먹은 패티의 수를 구하는 문제입니다.
  레벨-N 버거는 B[레벨-N-1버거]P[레벨-N-1버거]B로 이루어져 있습니다.
  레벨-0 버거는 P입니다.

접근법

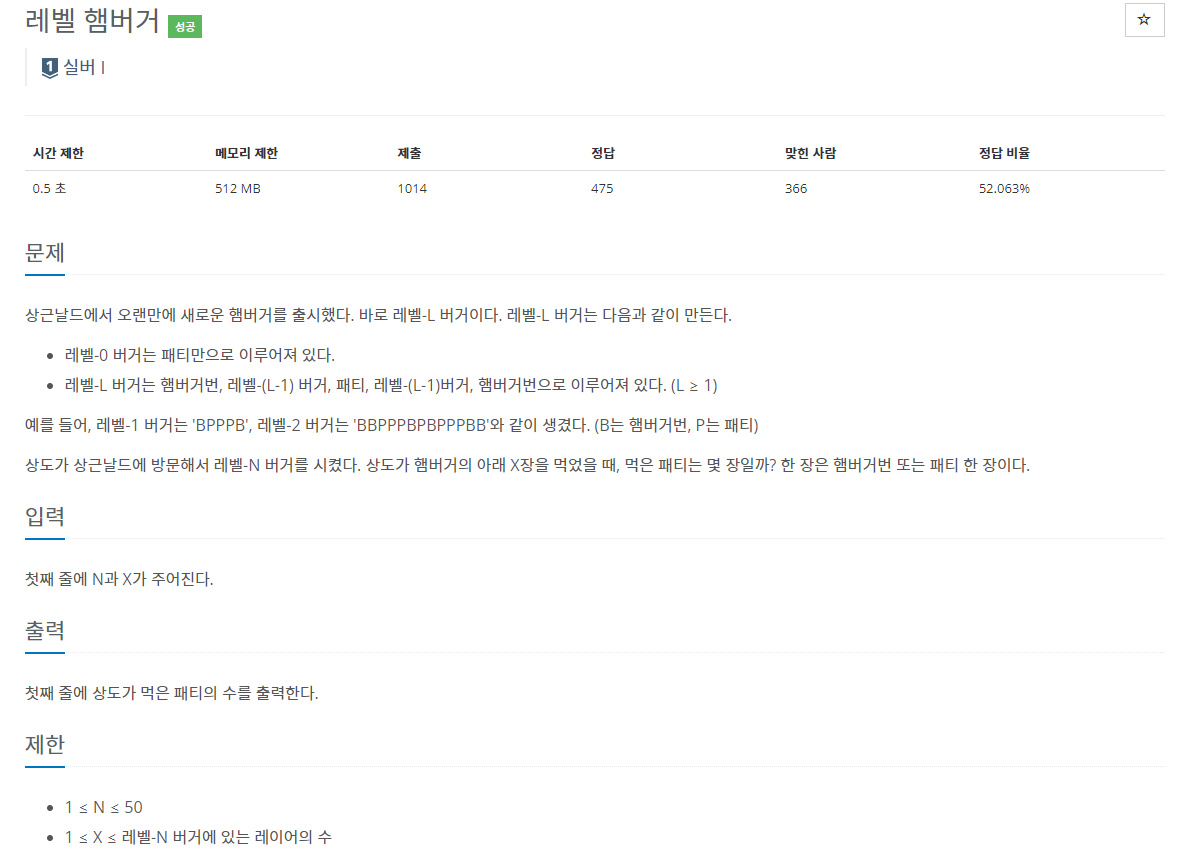
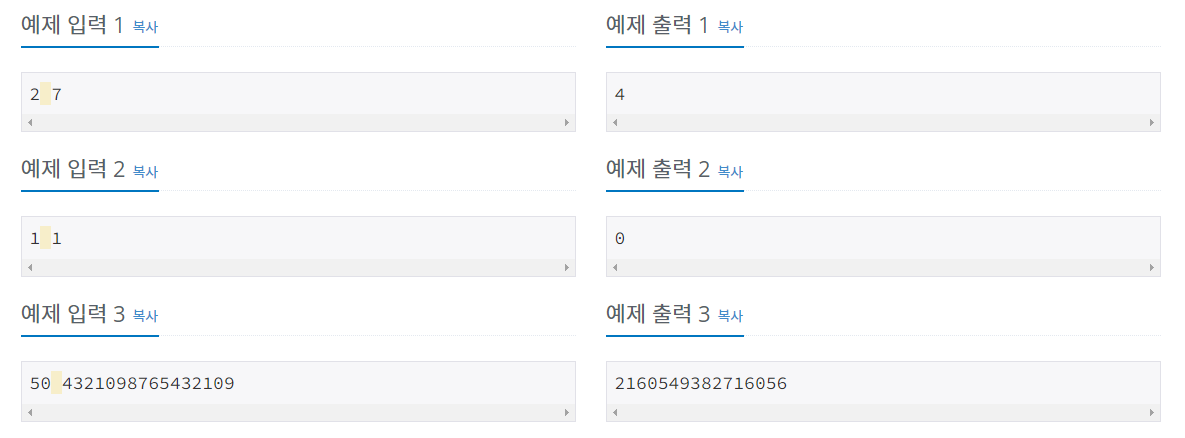
• 재귀를 이용해 문제를 해결할 수 있습니다. 재귀 코드의 핵심은 기저조건을 잘 구하는 것입니다. 이 문제에서 레벨0버거의 패티 개수는 1개라는 것이 기저조건입니다.
  버거를 만드는 방법을 통해 레벨N버거 전체의 길이와 패티의 개수를 구할 수 있습니다.
  레벨N버거의 길이: (레벨N-1버거의 길이 * 2) + 3
  레벨N버거의 패티수: (레벨N-1버거의 패티 수 * 2) +1
• X의 값을 5가지 구간으로 나눌 수 있습니다.
  • X == 1: 레벨0을 제외하면 항상 빵이기 때문에 패티를 하나도 먹지 못합니다.
  • 1 < X < mid: 레벨N-1버거에서 앞에서부터 X개를 먹는것과 비슷합니다. 비슷하다고 표현한 이유는 앞에 빵이 하나 추가되어 있기 때문입니다.
  • X == mid: 레벨N버거는 B[레벨N-1]P[레벨N-1]B형태이기 때문에 mid번째 값은 항상 P입니다. 또한 mid까지 먹었을 때 패티의 양은 레벨N-1버거의 패티의 양 + 1입니다.
  • mid < X < 레벨N버거의 길이: 레벨N-1버거의 패티의 양 + 1개를 먹고 레벨N-1버거에서 앞에서부터 X-mid개를 먹는것과 동일합니다.
  • X == 레벨N버거의 길이: 레벨N버거 속 패티의 양과 동일합니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	static long[] burgerLength;
	static long[] pattyCnt;
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		long X = Long.parseLong(st.nextToken());

		burgerLength = new long[N+1];
		burgerLength[0] = 1L;
		for (int i = 1; i <= N; i++) {
			burgerLength[i] = burgerLength[i-1]*2+3;
		}
		
		pattyCnt = new long[N+1];
		pattyCnt[0] = 1L;
		for (int i = 1; i <= N; i++) {
			pattyCnt[i] = pattyCnt[i-1]*2+1;
		}
		
		System.out.println(recursion(X,N));
	}
	
	public static long recursion(long X, int level) { // X는 0부터 시작하는 index가 아닌 1부터 시작하는 값입니다.
    	// 기저조건
		if(level == 0) return 1L;
		if(X <=1) return 0L;
		
		long mid = burgerLength[level-1]+2;
        
        // level빵 전체를 먹는 경우
		if(X == burgerLength[level]) return pattyCnt[level]; 
        // mid번째까지만 먹는 경우
		if(X == mid) return pattyCnt[level-1]+1; 
        // 처음에 빵이 껴있기 때문에 X가 아닌 X-1을 해줍니다. 
		if(0 < X && X < mid) return recursion(X-1,level-1); 
        // pattyCnt[level-1]+1에 처음있는 빵이 포함되어 있기 때문에 재귀함수에서 X-mid에 -1을 해줄 필요가 없습니다.
        // X = mid+1인 경우를 잘 생각해보면 됩니다.(이때 Level-1버거의 0이 아닌 1을 가리켜야 합니다.)
		if(mid < X && X < burgerLength[level]) return pattyCnt[level-1]+1+recursion(X-mid,level-1);
		
		return -1;
		
	}
	
}