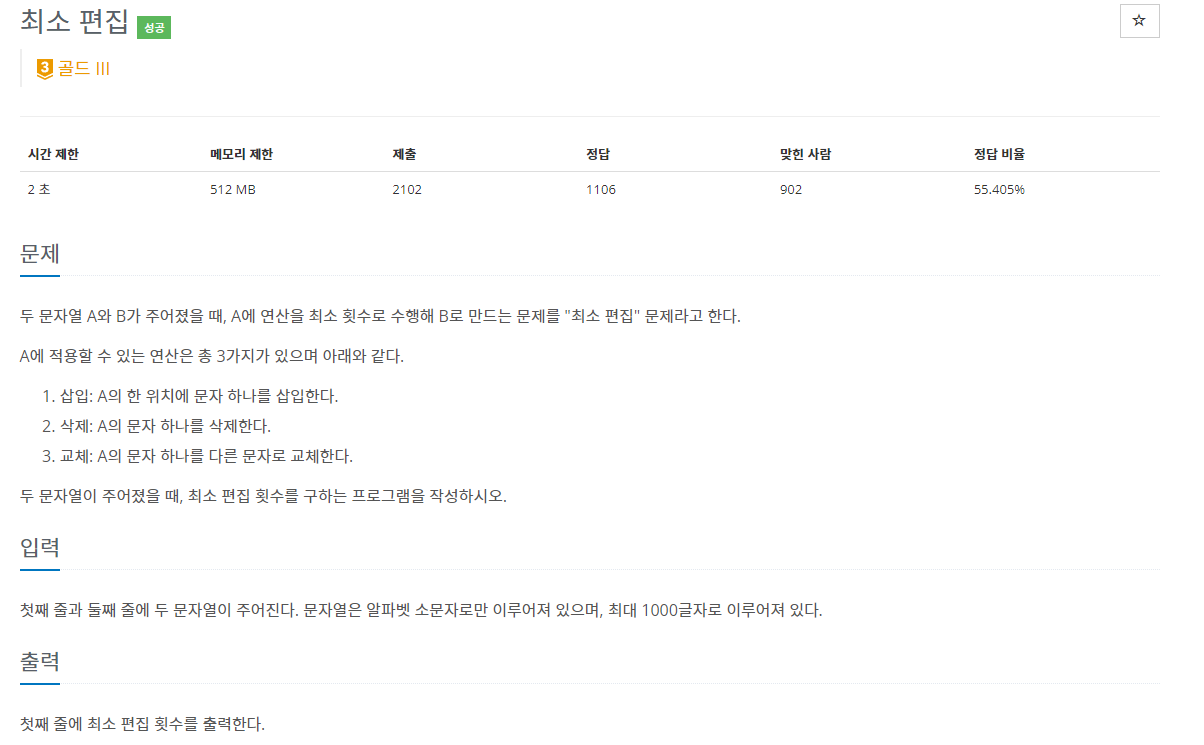
문제 설명
접근법
-
최장 공통 부분 수열(LCS)에 대한 이해가 필요합니다. LCS를 잘 모르는 분들은 백준 17218번: 비밀번호 만들기를 먼저 풀어보는 걸 추천드립니다.
-
dp[i][j] =
문자열1의 i까지를문자열2의 j까지로 만들기 위해 필요한 최소연산 입니다. 우선 단순한 예제를 직접 실행해 보겠습니다. 왼쪽 문자열에서 오른쪽 문자열을 만든다고 생각하고 풀었습니다.- a b c c X1 X2 X3 b X4 X5 X6 a X7 X8 X9 X1:
c를a로 바꿔야 합니다.c를a로교체합니다. (1)
X2:c를ab로 바꿔야 합니다.c를a로교체하고,b를추가합니다. (2)
X3:c를abc로 바꿔야 합니다.a를추가하고,b를추가합니다. (2)X4:
cb를a로 바꿔야 합니다.삭제로b를 지우고,c를a로교체합니다. (2)
X5:cb를ab로 바꿔야 합니다.c를a로교체합니다. (1)
X6:cb를abc로 바꿔야 합니다.c를a로교체하고,c를추가합니다. (2)X7:
cba를a로 바꿔야 합니다.삭제로c를 지우고,삭제로b를 지웁니다. (2)
X8:cba를ab로 바꿔야 합니다.c를a로교체하고, 뒤에 있는a를삭제합니다. (2)
X9:cba를abc로 바꿔야 합니다.c를a로교체하고, 뒤에 있는a를c로교체합니다. (2)완성된 모양은 다음과 같습니다.
- a b c c 1 2 2 b 2 1 2 a 2 2 2 -
중요한 건 앞의 계산이 모두 진행되었다고 가정하고
문자열1의 i번째 문자와 문자열2의 j번째 문자를 비교하는 것입니다. 편의상 문자열1의 i번째 문자를S1_i, 문자열2의 j번째 문자를S2_j라고 하겠습니다.S1_i과S2_j가 같으면 연산이 필요하지 않습니다.cb를ab로 바꾸는X5에서 S1_i와 S2_j가 같았기 때문에c를a로 바꾸는X1연산과 시행 횟수가 동일합니다.
dp[i][j] = dp[i-1][j-1]S1_i과S2_j가 다르면 연산이 필요합니다. 앞의 계산이 모두 진행되었다고 가정한 채로(앞의 문자들은 모두 해당 횟수만큼 사용해 같은 문자로 변경된 상태로) 마지막 문자를삭제또는추가또는교체하면 원하는 문자열을 만들 수 있습니다. 세 가지 방법 중 가장 연산횟수가 적은 방식을 선택하면 됩니다.삭제연산을 한다는건dp[i][j-1] + 1과 동일합니다.추가연산을 한다는건dp[i-1][j] + 1과 동일합니다.교체연산을 한다는건dp[i-1][j-1] + 1과 동일합니다.
정답
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s1 = br.readLine();
String s2 = br.readLine();
int[][] dp = new int[s1.length()+1][s2.length()+1];
// padding
for (int i = 0; i < dp.length; i++) {
dp[i][0] = i;
}
for (int i = 0; i < dp[0].length; i++) {
dp[0][i] = i;
}
for (int i = 1; i < s1.length()+1; i++) {
for (int j = 1; j < s2.length()+1; j++) {
if(s1.charAt(i-1) == s2.charAt(j-1)) {
dp[i][j] = dp[i-1][j-1];
}else {
dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]),dp[i-1][j-1])+1;
}
}
}
System.out.println(dp[s1.length()][s2.length()]);
}
} 
