백준 1915번: 가장 큰 정사각형

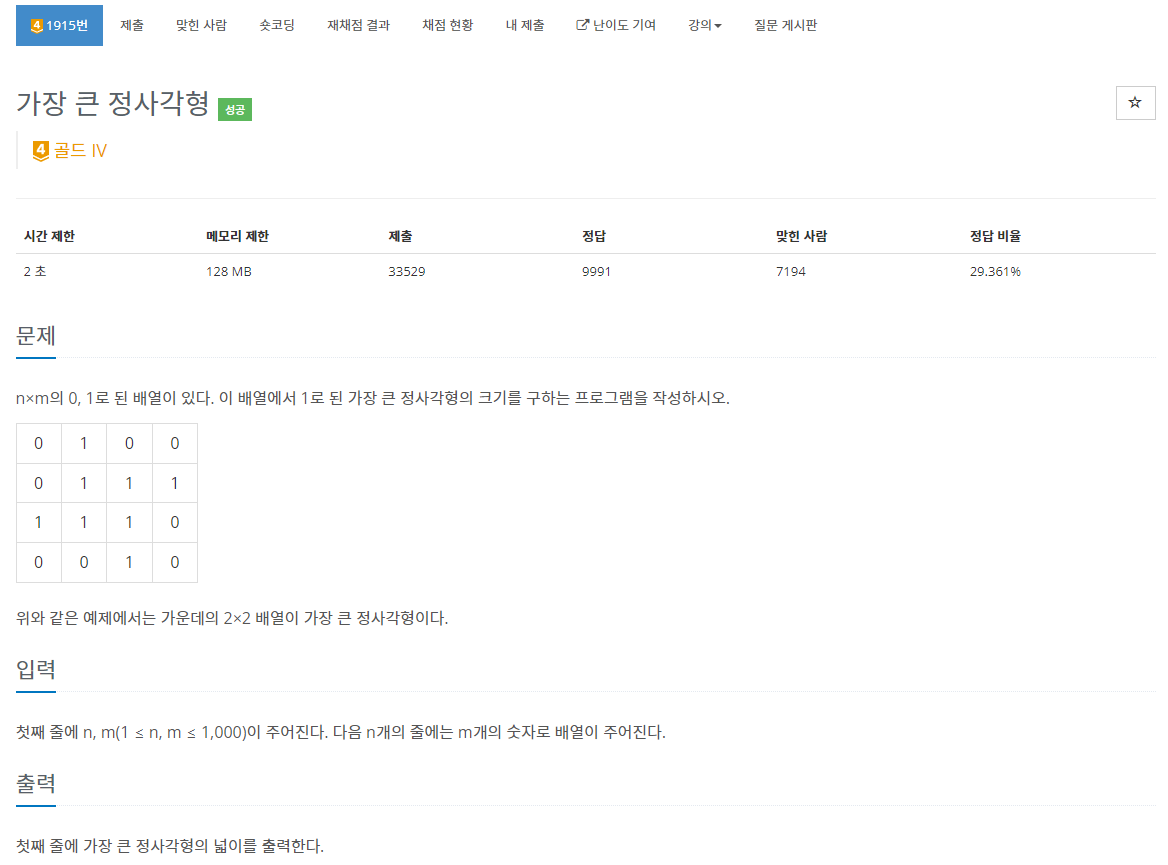
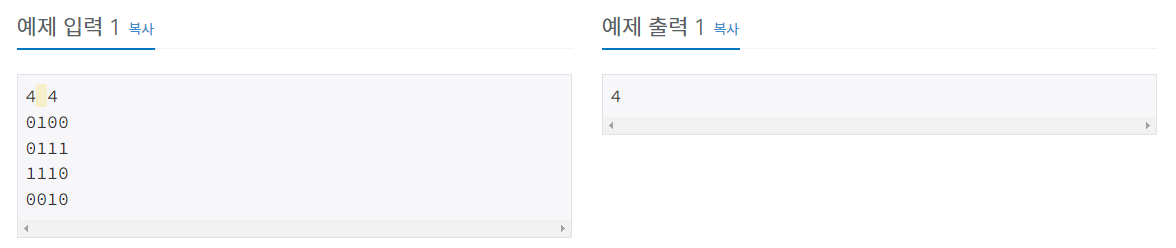
문제 설명

• https://www.acmicpc.net/problem/1915
• 1로만 이루어진 가장 큰 정사각형의 넓이를 구하는 문제입니다.

접근법

가장 먼저 브루트포스 접근법이 떠올랐습니다. 하지만 O(n^4)의 시간복잡도가 예상되어 시도하지 않았습니다.
다음으로 누적합을 이용했습니다. 누적합의 값이 x^2이면 정사각형이라는 의미입니다. 이 경우에도 모든 값이 1인 경우 O(n^3)의 시간복잡도로 시간초과가 발생했습니다.

dp를 활용해 문제를 풀 수 있습니다. dp[i][j] = (i,j)를 마지막 꼭지점으로하는 가장 큰 정사각형 한 변의 길이로 설정할 수 있습니다.

• board[i][j]가 0이면 dp[i][j]도 0입니다.
• dp[i][j]는 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]의 영향을 받습니다. 세 값중 가장 작은 값에 1을 더한 값이 dp[i][j]가 됩니다.
  • 왼쪽, 왼쪽 대각선, 위쪽이 모두 1일 때 dp[i][j]는 2가 됩니다.
    
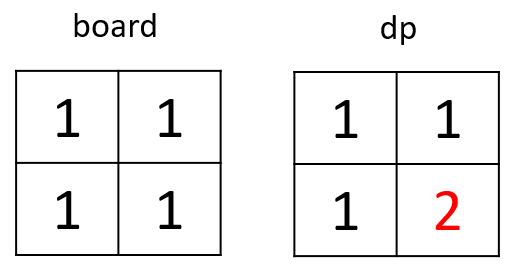
  • 정사각형은 가로, 세로, 대각선 모두 값을 가져야 하기 때문에 세 방향 중 가장 짧은 값을 dp[i][j]는 가지게 됩니다.
    
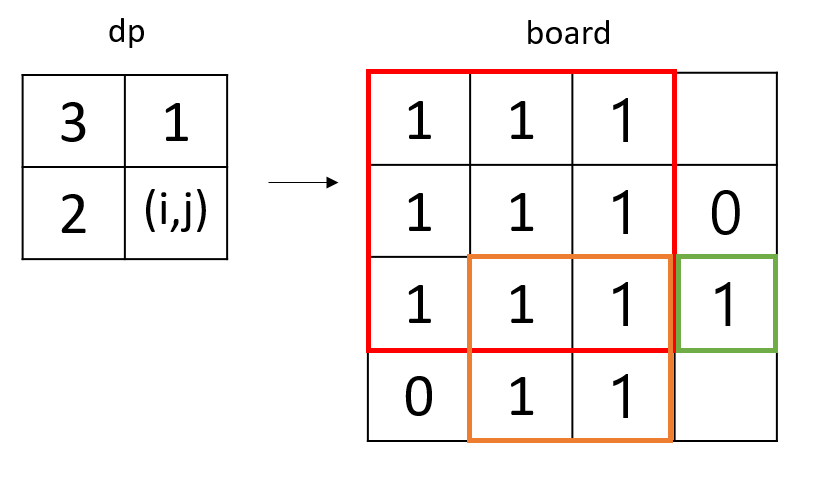
    • dp배열로 원배열을 유추해보면 다음과 같은 모양일 겁니다. 이때 dp[i-1][j]의 값이 1로 가장 적기 때문에 아무리 주변의 값이 커도 dp[i][j]에서 만들 수 있는 정사각형은 가장 작은 값(dp[i-1][j])에 의해 결정됩니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int[][] board = new int[N][M];
		for (int i = 0; i < N; i++) {
			String s = br.readLine();
			for (int j = 0; j < M; j++) {
				board[i][j] = s.charAt(j)-'0';
			}
		}
		int maxVal = 0;
		
		int[][] dp = new int[N+1][M+1];
		dp[1][1] = board[0][0];
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= M; j++) {
				if(board[i-1][j-1] == 0) continue; // dp[i][j] = 0 이랑 같음
				dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]),dp[i-1][j-1])+1;
				maxVal = Math.max(maxVal, dp[i][j]);
			}
		}
		
		System.out.println(maxVal*maxVal);
		
//		for (int i = 0; i < dp.length; i++) {
//			System.out.println(Arrays.toString(dp[i]));
//		}
	}

}