백준 1947번: 선물 전달

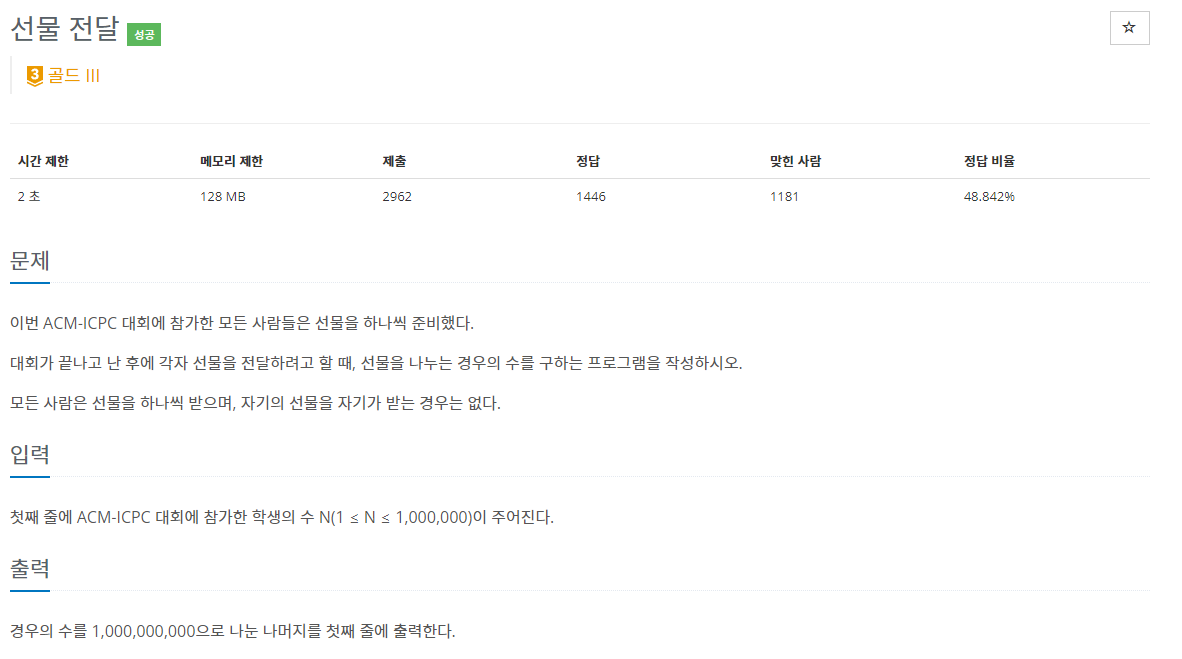
문제 설명

• https://www.acmicpc.net/problem/1947

접근법

• 완전순열 또는 교란순열이라 불리는 문제입니다.
  1번부터 N명의 사람이 있을 때 어떤 사람 x를 기준으로 생각해 봅시다.
  x는 자신의 '누군가'에게 선물을 주고, 또 '누군가'로부터 선물을 받습니다. 여기서 두 가지 경우를 생각할 수 있습니다.
  첫 번째는 x가 선물을 준 사람과 x에게 선물을 준 사람이 동일인인 경우입니다. 그러면 둘을 제외한 나머지 사람들끼리 선물을 나눠가지는 것과 경우의 수가 동일합니다.
  이는 N-2명의 사람이 각자 자신의 선물이 아닌 다른 선물을 갖는 경우의 수인 dp[n-2] 입니다. x와 선물을 주고받는 사람은 x외 N-1명이 가능하기 때문에 총 경우의 수는 (n-1)*dp[n-2]입니다.
  두 번째는 x가 선물을 준 사람과 x에게 선물을 받은 사람이 다른 경우입니다. 이 과정을 조금 세분화 해 x가 누군가에게 선물을 줬지만 아직 선물을 받지 않은 경우를 떠올려 봅시다. 아마 아래와 같을 겁니다.
  
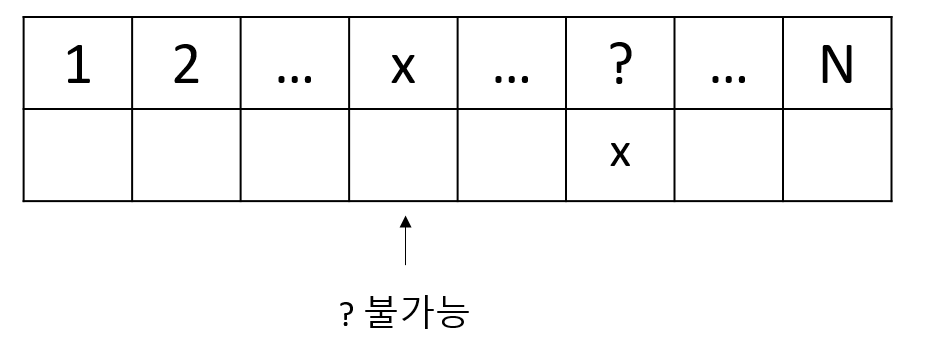
  ?칸은 이미 x로 채워졌으니 이렇게 N-1칸을 채워야 하는 상황일 겁니다. 여기서 ?가 불가능한 x칸을 ?로 바꿔 생각해도 됩니다. (이 문제는 i번째 칸이 숫자 i를 가지지 못하는 문제입니다. 그런데 x번째 칸이 숫자 ?를 가지지 못하니 이는 x번째 칸이 ?번째 칸과도 같다는 의미입니다.)
  이는 N-1명의 사람이 각자 자신의 선물이 아닌 다른 선물을 갖는 경우의 수인 dp[n-1] 입니다. x의 선물을 받는 ?는 x외 N-1명이 가능하기 때문에 총 경우의 수는 (n-1)*dp[n-1]입니다.
  
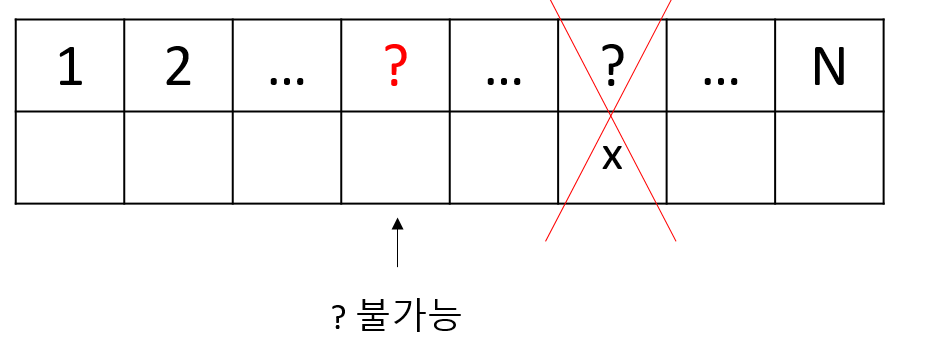
  위 첫번째 경우와 두번째 경우는 동시에 발생할 수 없으며, 두 경우의 수 외에 다른 경우의 수는 존재하지 않습니다. 그렇기 때문에 x를 기준으로 발생할 수 있는 모든 경우의 수는 (n-1)*(dp[n-2] + dp[n-1])입니다.

정답

import java.util.*;
import java.io.*;

public class Main {
	static int cnt = 0;
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int divNumber = 1_000_000_000;
		
		long[] dp = new long[Math.max(3,N+1)];
		dp[2] = 1L;
		for (int i = 3; i <= N; i++) {
			dp[i] = ((i-1)*(dp[i-1]+dp[i-2]))%divNumber;
		}
		System.out.println(dp[N]);
		
	}
}