백준 2239번: 스도쿠

문제 설명

• https://www.acmicpc.net/problem/2239
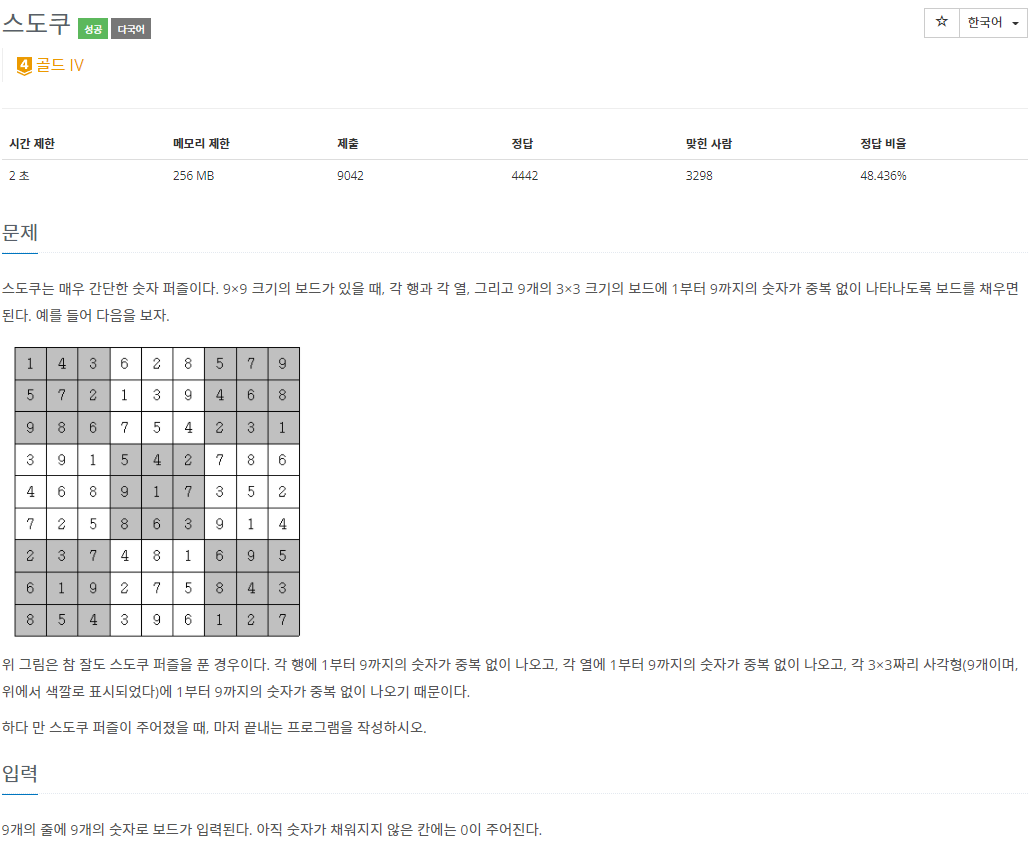
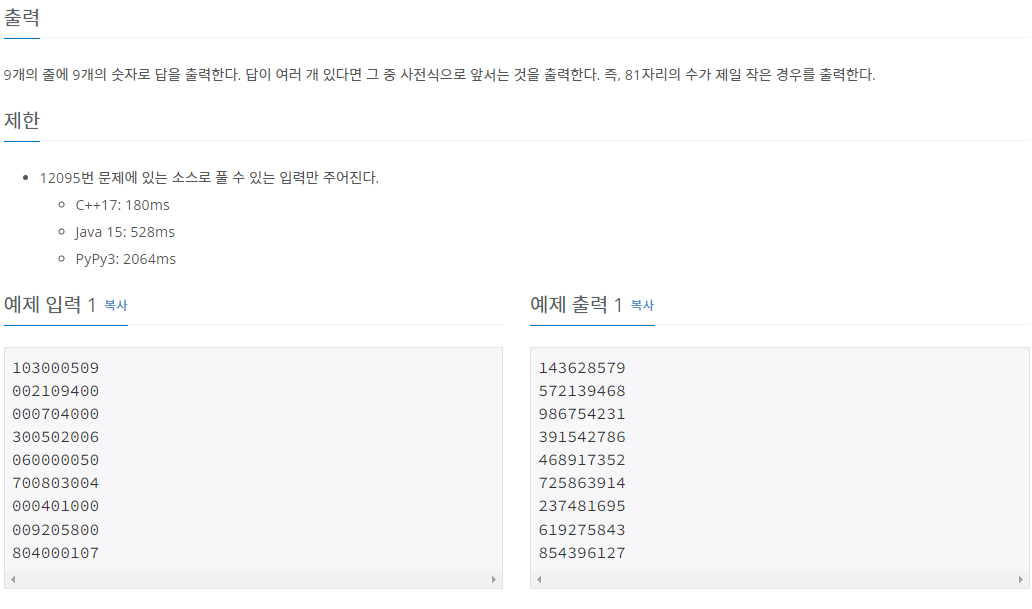
• 스도쿠를 완성해야 합니다.

접근법

• 백트래킹을 활용할 수 있습니다.
  • (x,y)위치에서 1,2,3,4,5,6,7,8,9 중 가능한 숫자를 넣어보고 다음 숫자를 채우러 갑니다.
  • 스도쿠의 규칙을 벗어나면 다시 되돌아와 다음 숫자를 넣어봅니다.
  • 해당 depth에서 가장 처음 만난 빈칸만 확인하고, 나머지 빈칸은 더 깊은 depth에서 확인하면 됩니다.

a b c	// a,b,c는 모두 0을 의미하며, depth가 0일 때 -> a의 값만 1,2,3 해보면 됩니다.
1 2 3 
2 3 1

1 b c	2 b c	3 b c 
1 2 3	1 2 3	2 3 1
2 3 1	2 3 1	2 3 1  // 이렇게 3가지 경우만 고려하면 되지

a 1 c	a 2 c	a 3 c 
1 2 3	1 2 3	2 3 1
2 3 1	2 3 1	2 3 1  // 이러한 경우와(b를 고려)

a b 1	a b 2	a b 3 
1 2 3	1 2 3	2 3 1
2 3 1	2 3 1	2 3 1 // 이러한 경우(c를 고려)를 고려할 필요는 없습니다.

유의사항

• 가지치기를 고려하지 않으면 매우 오랜 시간이 걸립니다.
• 빈칸이 N개일 때 각 빈칸에 9개의 숫자를 넣어볼 수 있기 때문에 9^N의 시간이 걸릴 수 있습니다.
• 해당 위치에서 가능한 원소를 직접 list로 return하는 것보다 어떤 원소가 가능한지를 확인하는 게 훨씬 효율적입니다.
  • 가로,세로,사각형을 보니깐 여기는 {1,7}이 들어갈 수 있겠군. X
  • 1~9까지 넣어보니깐 되는게 1 또는 7이구나. O
• list를 return하는 방식이 어려운 이유는 고려해야 할 사항이 많기 때문입니다.
  • 한 예로 가로검사에서 {1,4}, 세로검사에서 {1}, 사각형검사에서 {1,2,3,4,5,6,7,8,9}가 가능하다고 나왔다면 1만 return해야 합니다.

pseudocode

Validate(x,y,c,board){
	(x,y)의 가로줄에 c가 있다면 return false;
	(x,y)의 세로줄에 c가 있다면 return false;	
    (x,y)가 포함된 3x3사각형에 c가 있다면 return false;
    위 3 조건을 모두 피해왔다면 return true
}

BackT(){
	if(모든 빈칸을 규칙에 맞게 다 채웠다면){
    	정답출력
        return;
    }

	for(i->1~9){ // 가로
    	for(j->1~9){ // 세로
        	if(현재 칸에 숫자가 채워져 있다면) continue;
        	for(c->1~9){
            	if(Validate(i,j,c,board)){ // 현재의 빈칸을 c로 채울 수 있다면
                	(i,j)를 c로 채우고
                    BackT(depth+1,board) // 다음 빈칸을 채우러 갑니다.
                    현재 (i,j)에서 또 다른 c가 가능한지 확인하기 위해 0으로 리셋시킵니다.
                    
                }
            }
            return false; // depth하나당 하나의 빈칸만 채웁니다.
        } 
    }
}

정답

import java.io.*;
import java.util.*;

public class Main {
	static int N = 9;
	static int ZeroCnt = 0;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = null;

		int[][] board = new int[N][N];
		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());
			char[] temp = st.nextToken().toCharArray();
			for (int j = 0; j < N; j++) {
				if (temp[j] == '0')
					ZeroCnt++;
				board[i][j] = temp[j] - '0';
			}
		}
		BackT(0, board);
	}


	public static boolean Validate(int x, int y, int c, int[][] board) {
		for (int i = 0; i < N; i++) { // 가로검사와 세로검사
			if (board[x][i] == c) return false; 
			if (board[i][y] == c) return false;
		}
		
		// 사각형 검사
		int startX = 3 * (x / 3);
		int startY = 3 * (y / 3);
		for (int i = startX; i < startX + 3; i++) {
			for (int j = startY; j < startY + 3; j++) {
				if (board[i][j] == c)
					return false;
			}
		}
		return true;
	}

	public static boolean BackT(int depth, int[][] board) {
		if (depth == ZeroCnt) { // 모든 0을 규칙에 맞게 채웠다면
			for (int i = 0; i < board.length; i++) {
				StringBuffer sb = new StringBuffer();
				for (int j = 0; j < N; j++) {
					sb.append(board[i][j]);
				}
				System.out.println(sb.toString());
			}
			return true;
		}
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				if (board[i][j] != 0) continue; // 이미 채워진 공간은 고려하지 않습니다.
				for (int c = 1; c <= 9; c++) { // 어떠한 빈칸에서 1~9까지 숫자를 고려해 봅니다.
					if (Validate(i, j, c, board)) { // 숫자c를 넣었을 때 아무런 이상이 없다면
						board[i][j] = c; // c를 넣어봅니다
						if (BackT(depth + 1, board)) return true; // 다음 빈칸을 찾으러 갑니다.
						board[i][j] = 0; // 가능한 다른c를 넣기 위해 0으로 바꿔줍니다.
					}
				}
				// 처음 만나는 0만 채우고 다른 0은 depth가 더 깊은 곳에서 채우면 되기 때문에 return 합니다.
				return false;

			}
		}
		return false;
	}

}