백준 17471번: 게리맨더링

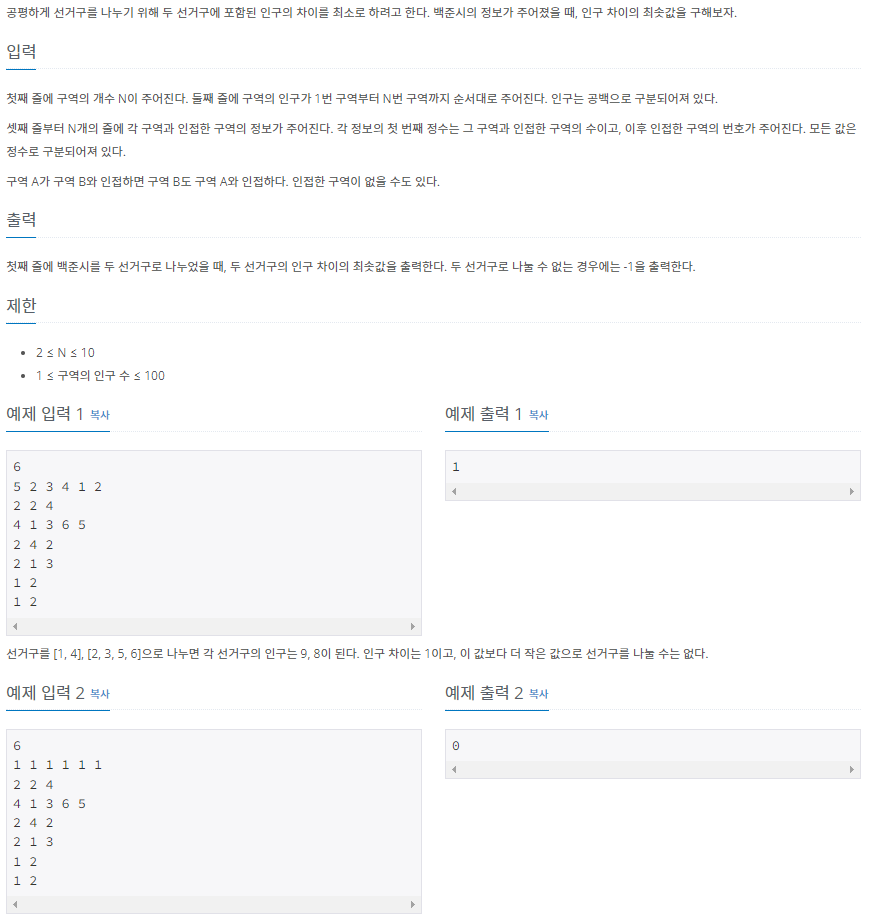
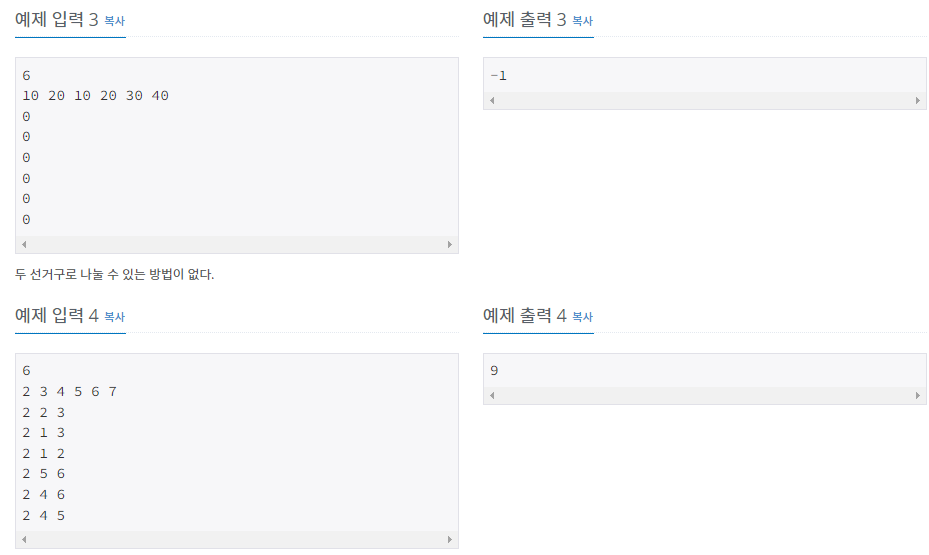
문제 설명

• https://www.acmicpc.net/problem/17471
• 주어진 그래프를 이동이 가능한 두 개의 그룹으로 나누었을 때, 두 그룹의 인구 차이가 가장 적게 나도록 만드는 문제입니다.

접근법

• 선거구를 두 개의 집합으로 나누는 방법을 부분집합으로 구합니다.
• 나누어진 선거구가 실제로 연결되어 있는지 확인합니다.
• 저는 서로 다른 진영의 다리를 끊고, 남은 다리들로 true측과 false측이 하나로 묶일 수 있는지를 확인했습니다.

입력 그래프가 {0=[1, 3], 1=[0, 2, 5, 4], 2=[3, 1], 3=[0, 2], 4=[1], 5=[1]}일 때

부분집합의 결과로 [true, true, true, true, false, false] 를 얻었다면, 0123을 하나로 묶고 45를 하나로 묶습니다.

다른 진영으로의 다리를 끊은 그래프는 {0=[1, 3], 1=[0, 2], 2=[3, 1], 3=[0, 2], 4=[], 5=[]} 가 됩니다.
	* key값이 0123인 곳의 원소에는 45가 없고, key값이 45인 곳의 원소에는 0123이 없습니다.

pseudocode

SubSet(dpth){
	if(depth == n){ // 하나의 부분집합이 완성되면
    	if(두 개의 그룹이 아니라 하나의 그룹이라면)return;
        
        // 서로 다른 지역으로 가는 다리는 끊어버립니다.
        for(map.keySet()){
        	if(v[key]==true면){
            	map.get(key)속에 있는 v[원소]=false인 원소값 모두 제거
            }else{
            	map.get(key)속에 있는 v[원소]=true인 원소값 모두 제거
            }
        } // 다른지역으로의 다리를 모두 끊고 나서
        
        key가 가진 value들과 union을 진행합니다.
        if(ConnectCheck){ // union을 진행한 결과 딱 두 덩이로 나뉜다면
        	두 지역의 인구수 차이를 구합니다.
        } 
        return;
    }
	
    // depth번째가 true인 부분집합
    v[depth] = true;
    SubSet(depth+1);
    
	// depth번째가 false인 부분집합
	v[depth] = false;
    SubSet(depth+1);
}

ConnectCheck(){
	for(모든 key값을 돌면서){
    	if(key가 true그룹인데){
        	가장 먼저 나오는 true그룹 key의 부모를 대표 parent로 설정
        	if(true그룹의 대표 parent값 != key의 parent값) return false;
        }
        
        if(key가 false그룹인데){
            가장 먼저 나오는 false그룹 key의 부모를 대표 parent로 설정
			if(false그룹의 대표 parent값 != key의 parent값) return false;
        }
    }
    return true; // true그룹은 하나의 parent로 연결되어 있고, false그룹도 하나의 parent로 연결되어 있음

}

정답

import java.io.*;
import java.util.*;

public class Main {
	static int N;
	static int[] parent,population;
	static HashMap<Integer,List<Integer>> map = new HashMap<Integer,List<Integer>>();
	static int MinVal = Integer.MAX_VALUE;
	public static void main(String[] args) {
		// 입력값 세팅
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		population = new int[N];
		parent = new int[N];
		for (int i = 0; i < N; i++) {
			population[i] = sc.nextInt();
			parent[i] = i;
		}
		
		
		for (int i = 0; i < N; i++) {
			map.put(i, new LinkedList<Integer>());
			int n = sc.nextInt();
			for (int j = 0; j < n; j++) {
				int b = sc.nextInt();
				map.get(i).add(b-1);
			}
		}
		

		SubSet(0,new boolean[N]);
		
		// 정답 출력
		if(MinVal == Integer.MAX_VALUE) {
			System.out.println(-1);
		}else {
			System.out.println(MinVal);
		}
	}

	public static void SubSet(int depth,boolean[] v) {
		if(depth == N) {
			
			// 모든 원소가 하나의 집합으로 이루어져 있다면
			if(OneGroup(v)) return;
			
			// 그래프의 연결상태를 담은 map을 Cmap으로 deepcopy
			HashMap<Integer,List<Integer>> CMap = new HashMap<Integer,List<Integer>>();
			int[] Cparent = parent.clone();
			for (Integer key : map.keySet()) {
				CMap.put(key, new LinkedList<Integer>());
				for (int i = 0; i < map.get(key).size(); i++) {
					CMap.get(key).add(map.get(key).get(i));
				}
			}
			
			// 서로다른 묶음으로의 다리를 끊는 방식
			for (Integer key : CMap.keySet()) {
				// key가 true면 자신의 원소 속 false를 모두 제거
				if(v[key]) {
					for (int i = 0; i < CMap.get(key).size(); i++) {
						if(!v[CMap.get(key).get(i)]) {
							CMap.get(key).remove(i);
							i--;
						}
					}
				}else {
					// key가 false면 자신의 원소 속 true를 모두 제거
					for (int i = 0; i < CMap.get(key).size(); i++) {
						if(v[CMap.get(key).get(i)]) {
							CMap.get(key).remove(i);
							i--;
						}
					}
					
				}
			}
            
			// 남아있는 key-value로 union
			for (Integer key : CMap.keySet()) {
				for (int i = 0; i < CMap.get(key).size(); i++) {
					union(key,CMap.get(key).get(i),Cparent);
				}
			}
			
			// union은 순서에 따라  parent가 모두 반영되지 않을 수 있기 때문에 한번 더 실행
			for (int i = 0; i < Cparent.length; i++) {
				find_parent(i,Cparent);
			}
			
			// true는 true끼리, false는 false끼리 모두 연결될 수 있는지 확인
			if(ConnectCheck(Cparent,v)) {
				int Sum = 0;
				for (int i = 0; i < N; i++) {
					if(v[i]) Sum+=population[i];
					else Sum-=population[i];
				}
				MinVal = Math.min(MinVal, Math.abs(Sum));
			}
			
			return;
		} // if(depth == N) 끝
		
		v[depth] = true;
		SubSet(depth+1,v);
		
		v[depth] = false;
		SubSet(depth+1,v);
        
	}
	
	public static int find_parent(int x,int[] parent) {
		if(x == parent[x]) return x;
		return parent[x] = find_parent(parent[x],parent);
	}
	
	public static void union(int a, int b,int[] parent) {
		int pa = find_parent(a,parent);
		int pb = find_parent(b,parent);
		if(pa>pb) parent[pa] = pb;
		else parent[pb] = pa;
	}
	
	// 하나의 부모를 가진다 == 연결되어 있다 ( == 건너갈 수 있다)
	// true는 true끼리 모두 하나의 부모를 가지고 있으며, false는 false끼리 모두 하나의 부모를 가지고 있는지 확인
	public static boolean ConnectCheck(int[] Cparent, boolean[] v) {
		int TgroupParent = -1;
		int FgroupParent = -1;
		for (int i = 0; i < N; i++) {
			if(v[i]) {
				// 비교군 설정
				if(TgroupParent == -1) {
					TgroupParent = Cparent[i];
				}
				if(TgroupParent != Cparent[i]) return false;
			}
			
			if(!v[i]) {
				// 비교군 설정
				if(FgroupParent == -1) {
					FgroupParent = Cparent[i];
				}
				if(FgroupParent != Cparent[i]) return false;
			}
		}
		return true; 
	}
	
	// 전부 true이거나 전부 false인 경우 배제
	public static boolean OneGroup(boolean[] v) {
		for (int i = 0; i < v.length; i++) {
			if(v[0]!=v[i]) return false;
		}
		return true;
	}
	
}

기타

• 둘로나눈 뒤 BFS를 2번 실행했을 때의 인구수가 전체 인구수와 같은지를 비교하는 방식도 있습니다.
  • BFS2번 실행한 인구수 != 전체 인구수 -> 연결되어 있지 않은 지역이 존재한다는 의미입니다.