백준 2302번: 극장 좌석

문제 설명

• https://www.acmicpc.net/problem/2302
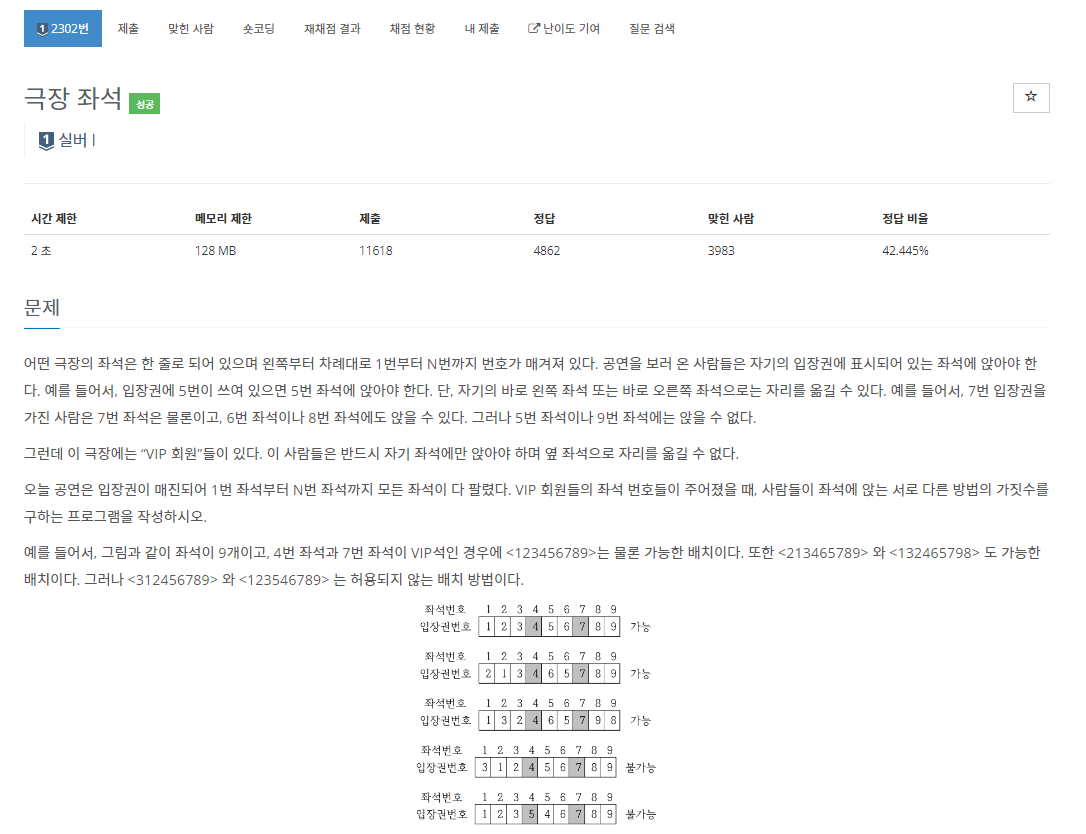
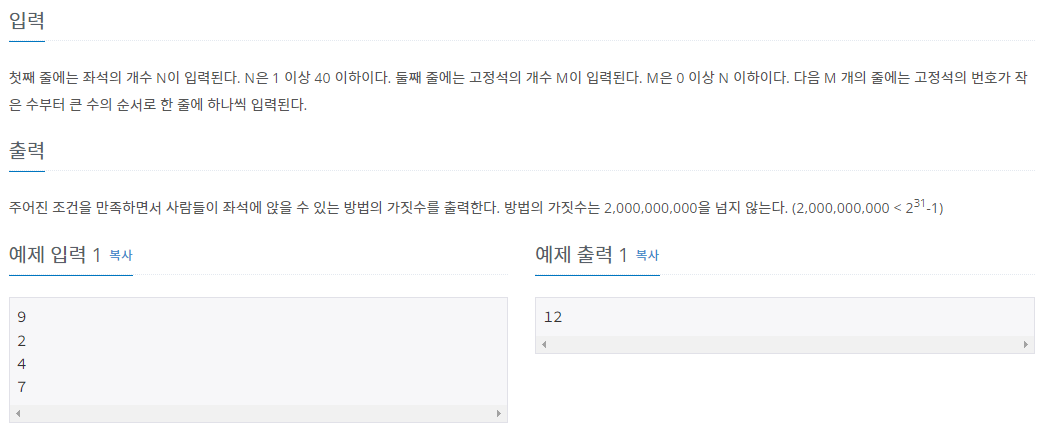
• N명의 사람이 N개의 좌석에 앉습니다. 기본적으로 N번째 사람은 N번째 자리에 앉아야 합니다. 일반인은 자신이 N번째일 때 N-1 혹은 N+1자리로 이동할 수 없습니다. VIP는 자리를 이동하지 못합니다.(N번째 사람은 반드시 N번째 자리에 앉아야 합니다.) 이때 N명의 사람이 앉을 수 있는 경우의 수를 구해야 합니다.

접근법

• 우선 VIP를 고려하지 않고 규칙을 유추해봅시다.

  • N=1명일 때 1만 가능합니다.

  • N=2명일 때 12,21이 가능합니다.

  • N=3명일 때 123,132,213이 가능합니다. 231은 불가능합니다.

  • N=4명일 때 1234,1243,1324,2134,2143이 가능합니다. 1342는 불가능합니다.

    • N번째 사람은 그대로 앉는다, 앞사람과 자리를 바꾼다 두 가지 선택이 가능합니다.
      뒷사람과 자리를 바꾸는 건 고려하지 않았습니다. N번째 사람이 뒷사람과 자리를 바꾸는 건 N+1번째 사람이 앞사람과 자리를 바꾸는것과 동일하기 때문입니다.
    • 1342는 132에서 4를 추가한 뒤 '앞사람과 자리를 바꾼다'에 해당합니다. 해당 경우가 안되는 이유는 2가 규칙을 이탈하기 때문입니다.
      즉, '앞사람과 자리를 바꾼다'는 조건은 N-1번째 숫자가 N-1일때만 가능합니다.
      반면 '그대로 앉는다'는 N-1번째 숫자와 무관하게 가능합니다.(1324)

  • 그래서 N명의 사람이 앉는 경우의 수 = N-1명의 사람이 앉는 경우의 수 + N-1명의 사람이 앉는 경우의 수 중에서 N-1번째 사람이 N-1번째 자리에 앉는 경우의 수라는 점화식이 성립합니다.

  • 

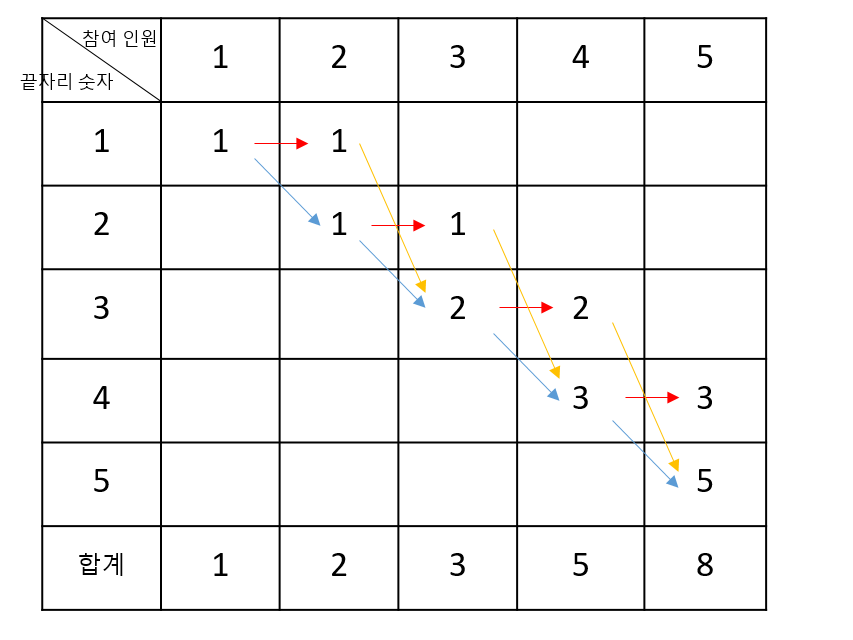
    • 빨간색 화살표는 N번째 사람이 N-1번째 사람과 자리를 바꾼 경우의 수 입니다.
    • 파란색과 노란색은 N번째 사람이 N-1번째 사람과 자리를 바꾸지 않는 경우의 수 입니다.
    • 제가 생각한 규칙은 2차원 배열이지만 합계만 따로 살펴봤을 때 피보나치규칙에 해당한다는 걸 알 수 있습니다.

• VIP를 고려하면 어떻게 될까요.

  • N-1명까지의 경우의 수가 k고 만약 N번째 사람이 VIP라면 경우의 수는 그대로 k입니다.
    • 단순히 뒤에 숫자N만 추가하기 때문에 경우의 수는 변화가 없습니다.
      4번째 사람이 vip라면 3번째 경우의 수(123,132,213)에서 뒤에 4만 추가합니다.(1234,1324,2134)
  • N번째 사람이 VIP라면 N+1번째 사람도 앞사람과 자리를 바꾸지 못합니다. 그래서 N+1번째 경우의 수도 그대로 k입니다.
    4번째 사람이 vip라면 4번째 경우의 수(1234,1324,2134)에서 뒤에 5만 추가해야 합니다.(12345,13245,21345)

저는 i번째 직전이 VIP였는지 판별하기 위해 token이라는 변수를 사용했습니다. i-1번이 VIP라면 token을 true로 둡니다. 해당 token은 i번을 검사할 때 활용되며 다시 false로 초기화됩니다. VIP거나 token이 true면 앞이랑 동일한 값을, 그렇지 않으면 피보나치로 값을 갱신해 줬습니다.

정답

import java.util.*;
import java.io.*;
import java.math.*;

public class Main {
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int M = Integer.parseInt(br.readLine());
		int[] arr = new int[M];
		for (int i = 0; i < M; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
        // 초기값
		long[] dp = new long[Math.max(3,N+1)];
		dp[0] = 1L;
		dp[1] = 1L;
		boolean token = false;
		if(isContains(arr,1)) { // 예외적으로 두자리숫자는 앞에 값(첫번째 값)이 VIP일때도 영향을 받음
			dp[2] = 1L;
		}else if(isContains(arr,2)) {
			dp[2] = dp[1];
			token = true;
		}else {
			dp[2] = dp[0] + dp[1];
		}
        
        // 시작
		for (int i = 3; i <= N; i++) {
			if(isContains(arr,i)) { // i번째가 VIP면
				token = true; 
				dp[i] = dp[i-1]; // 경우의 수는 증가하지 않는다
			}else {
				if(token) { // token이다 -> i-1번째가 VIP였다
					dp[i] = dp[i-1];
				}else {
					dp[i] = dp[i-1]+dp[i-2];
				}
				token = false; // 토큰 초기화
			}
		}
		System.out.println(dp[N]);
		
	}
	
	public static boolean isContains(int[] arr, int x) {
		for (int i = 0; i < arr.length; i++) {
			if(arr[i] == x) return true;
		}
		return false;
	}

}