백준 23885번: 비숍 투어

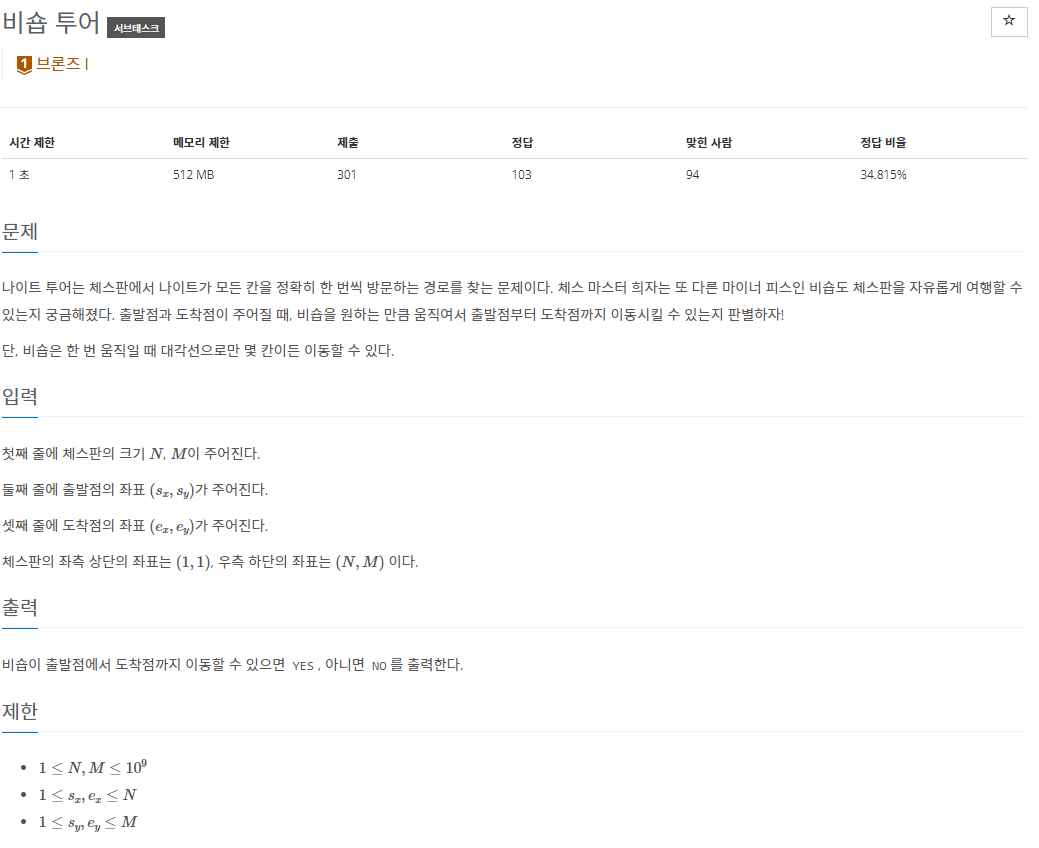
문제 설명

• (a,b)에 있는 비숍이 대각선으로만 이동했을 때 (c,d)에 도달할 수 있는지를 판단하는 문제입니다.
• 비숍은 현재 위치에서 ⤡ 또는 ⤢ 로 움직일 수 있습니다.
• 원하는 만큼 움직이기 때문에 움직이는 횟수의 제한은 없습니다.

접근법

아이디어

• 8x8 체스 판 위의 한 점에서 비숍이 도달할 수 있는 위치를 표현해 보겠습니다.
  
• 위 예제처럼 비숍이 도달할 수 있는 위치는 일정한 패턴을 보입니다. 이를 그림으로 표현하면 다음과 같습니다
  
• 회색 판 위의 비숍은 회색 판 어디든지 도달할 수 있으며, 검은 판 위에는 결코 도달할 수 없습니다.
• 검은 판 위의 비숍도 마찬가지로 검은 판 어디든지 도달할 수 있지만 회색 판 위에는 도달할 수 없습니다.
• 판 위에 좌표를 나열해보면 또 다른 규칙을 발견할 수 있습니다.
  

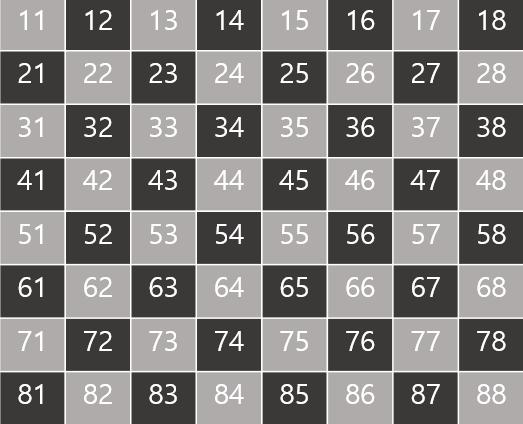
  • 흰색 판 위의 좌표들은 모두 행+열의 값이 짝수입니다.
  • 검은 판 위의 좌표들은 모두 행+열의 값이 홀수입니다.

• 따라서 (a+b)와 (c+d)가 둘 다 홀수, 혹은 둘 다 짝수라면 (a,b)에서 (c,d)로 이동할 수 있다는 결론을 도출할 수 있습니다.

예외

• 하지만 (a+b)와 (c+d)가 둘 다 홀수, 혹은 둘 다 짝수라면 (a,b)에서 (c,d)로 이동할 수 있다는 조건만으로 문제를 해결할 수 없습니다. 다음의 두 경우를 살펴보겠습니다.

• N 또는 M의 값이 1이 되면 비숍은 이동할 수 없습니다. (a+b)와 (c+d)가 둘 다 홀수, 혹은 둘 다 짝수라도 (a,b)에서 (c,d)로 이동할 수 없습니다.

  • 여기에는 또 하나의 예외가 발생합니다. N 또는 M의 값이 1이 되면 비숍은 이동할 수 없지만, 출발점과 도착점의 좌표가 동일하다면 우리는 출발점에서 도착점으로 비숍을 이동시킨 것과 같습니다.
  • 모든 조건에서 출발점과 도착점의 좌표가 동일하다면 이동이 가능한 것으로 판별해야 합니다.

• 즉 (a,b)와 (c,d)가 동일한 좌표인 경우와N또는 M이 1인 경우를 예외적으로 처리한 후(a+b)와 (c+d)가 둘 다 홀수, 혹은 둘 다 짝수라면 (a,b)에서 (c,d)로 이동할 수 있다라는 아이디어를 적용시켜야 합니다.

정답

N,M = list(map(int,input().split(' ')))
a,b = list(map(int,input().split(' ')))
c,d = list(map(int,input().split(' ')))

#시작점과 도착점이 일치하면 반드시 이동이 가능합니다
if min(a,b) == min(c,d) and max(a,b) == max(c,d):
    print("YES")
#가로 또는 세로가 1이면 이동이 불가능 합니다
elif min(N,M) == 1:
    print("NO")
#위 두 가지 경우를 아닐 때 (a,b)와 (c,d)가 같은 색 위에 있는지를 판단합니다 
elif (a+b)%2 == (c+d)%2: # 2로 나눈 나머지가 0이면 짝수, 2로 나눈 나머지가 1이면 홀수입니다
    print("YES")
else:
    print("NO")

느낀점

• 테스트케이스가 적은 상황에서 예외를 생각하기가 쉽지 않았다.