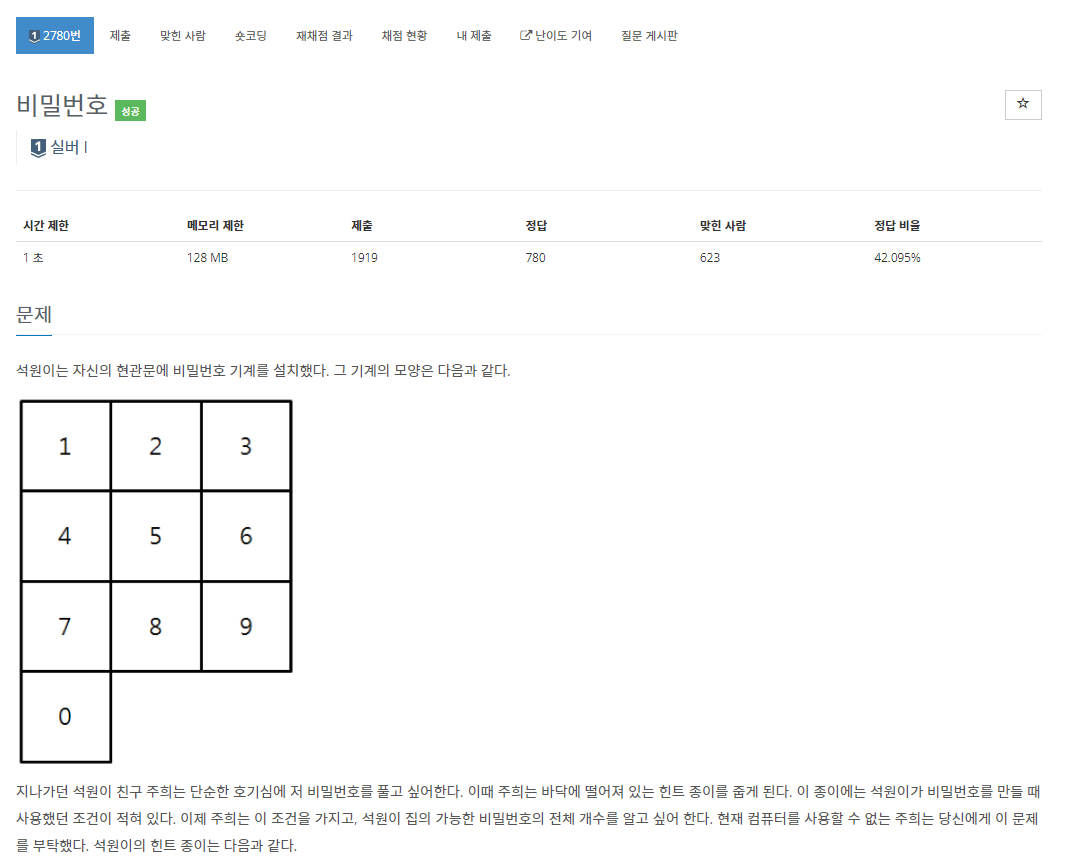
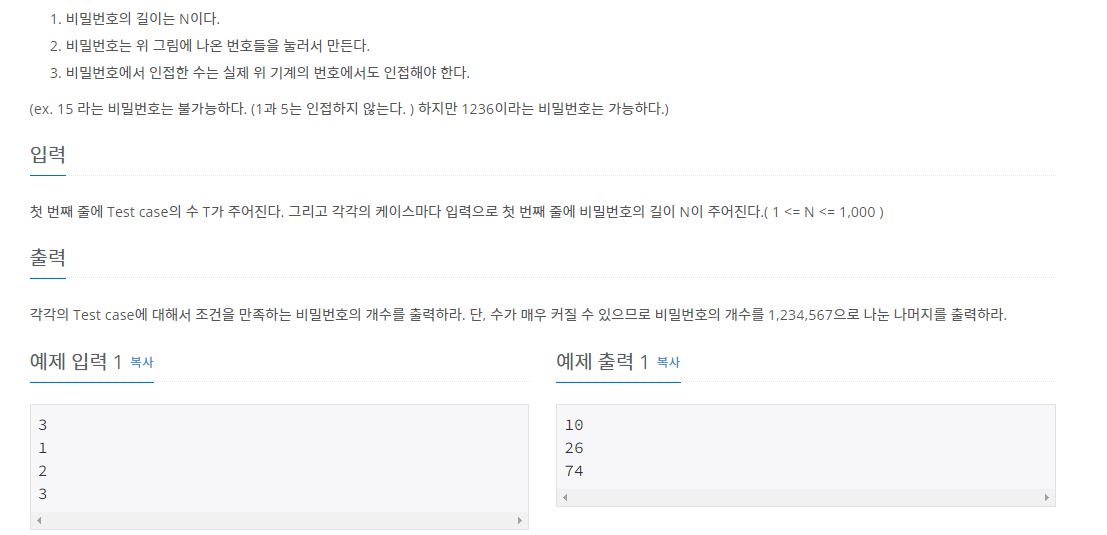
문제 설명
접근법
- 마지막 숫자가 뭐냐에 따라 다음으로 이동할 수 있는 경우의 수가 정해집니다.
- 길이가 N-1이고 문제의 조건을 만족하고 마지막이 4로 끝나는 숫자가 있다고 생각해 봅시다.
ex) N=4라면 길이가 3이고 인접한 번호로 연결되어 있으며 마지막이 4로 끝나는 숫자. 214, 874 등등이 있습니다. 214로 만들 수 있는 조건을 만족하는 숫자는 2141, 2145, 2147입니다. 4와 인접한 숫자가 1,5,7이기 때문입니다.
- 즉 dp[i][j]를
길이가 i면서 조건을 만족하는 숫자 중 j로 끝나는 숫자의 개수라고 정의할 때 dp[i]는 j와 인접한 dp[i-1][k]들에 의해 결정됩니다.(k는 j와 인접한 숫자)
정답
import java.util.*;
import java.io.*;
import java.math.*;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
int[][] dp = new int[1001][10];
Arrays.fill(dp[1], 1);
int divNum = 1_234_567;
for (int i = 2; i <= 1000; i++) {
dp[i][0] = dp[i-1][7]%divNum;
dp[i][1] = (dp[i-1][2]+dp[i-1][4])%divNum;
dp[i][2] = (dp[i-1][1]+dp[i-1][3]+dp[i-1][5])%divNum;
dp[i][3] = (dp[i-1][2]+dp[i-1][6])%divNum;
dp[i][4] = (dp[i-1][1]+dp[i-1][5]+dp[i-1][7])%divNum;
dp[i][5] = (dp[i-1][2]+dp[i-1][4]+dp[i-1][6]+dp[i-1][8])%divNum;
dp[i][6] = (dp[i-1][3]+dp[i-1][5]+dp[i-1][9])%divNum;
dp[i][7] = (dp[i-1][4]+dp[i-1][8]+dp[i-1][0])%divNum;
dp[i][8] = (dp[i-1][5]+dp[i-1][7]+dp[i-1][9])%divNum;
dp[i][9] = (dp[i-1][6]+dp[i-1][8])%divNum;
}
for (int t = 0; t < T; t++) {
int num = Integer.parseInt(br.readLine());
System.out.println((dp[num][0]+dp[num][1]+dp[num][2]+dp[num][3]+dp[num][4]+dp[num][5]+dp[num][6]+dp[num][7]+dp[num][8]+dp[num][9])%divNum);
}
}
}



