재귀 알고리즘

최창효·2022년 1월 9일

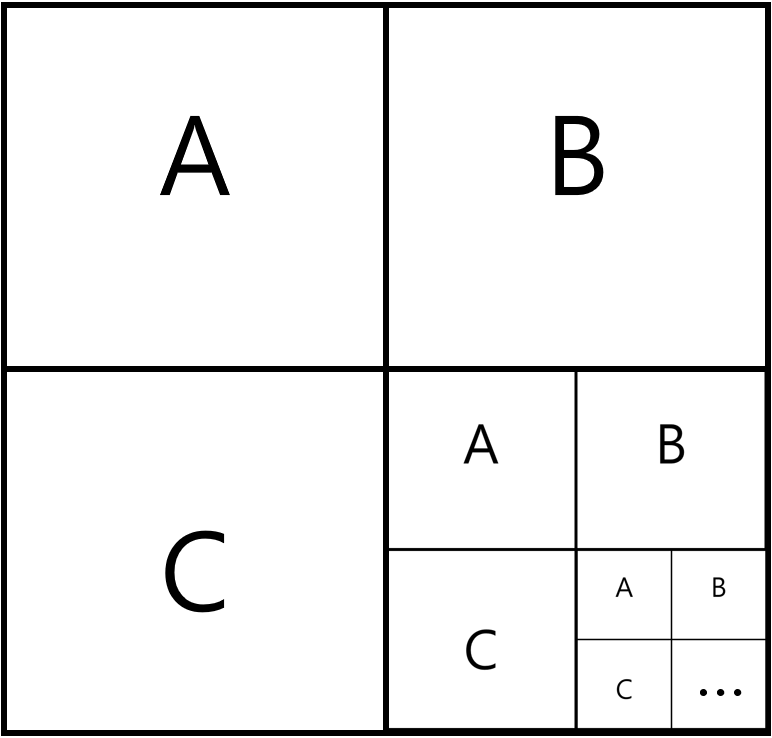
정의

재귀의 사전적 의미는 원래의 자리로 되돌아가거나 되돌아옴입니다.
컴퓨터 분야에서 재귀는 주어진 문제를 해결하기 위하여 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식를 뜻합니다.

형태

종료 조건

재귀함수는 계속해서 본인이 호출되는 함수입니다. 완전히 동일한 본인이 호출되어야 하지만 이해를 위해 호출 순서에 따라 번호를 부여해 생각해 보겠습니다.

함수를 실행하면서 본인을 호출합니다
호출된 본인이 실행되면서 본인(1)을 호출합니다
호출된 본인(1)이 실행되면서 본인(2)를 호출합니다
호출된 본인(2)가 실행되면서 본인(3)을 호출합니다 ...

-> 재귀함수는 특별한 조건을 설정해 두지 않으면 무한히 반복됩니다.

재귀함수에는 반드시 종료 조건이 포함되어야 합니다.

코드

재귀함수의 기본 형태는 다음과 같습니다.

def func(): #함수 정의
	if 종료조건:
	    break
	func()  #본인을 다시 호출

func() #함수 호출

재귀?

제 개인적인 경우 예제를 통해 재귀함수를 더 쉽게 이해할 수 있었습니다. 그래서 재귀 알고리즘의 이해를 도울 수 있는 예시를 몇 가지 살펴보겠습니다.

피보나치 수열

설명

피보나치 수열은 [0,1]로 시작해 앞선 두 원소의 합이 다음 원소가 되는 수열입니다.
$F(n) = F(n-1) + F(n-2) (n ≥ 2)$

f(n)을 구하는 과정에서 f(n-1)과 f(n-2)를 실행해야 합니다.
위 식은 f()함수에 들어가는 값이 n,n-1,n-2로 다른 것이지 f(n)을 위해 동일한 함수 f()를 호출해야 합니다.

코드

def fibo(n):
    # n의 값이 0또는 1이 되면 fibo함수는 더이상 자신을 호출하지 않습니다
    if n == 1:
        return 1
    
    if n == 0:
        return 0
    
    return fibo(n-1)+fibo(n-2) #fibo함수 안에서 fibo함수를 호출했습니다

fibo(3)를 구하기 위해 fibo(2)와 fibo(1)을 호출합니다
fibo(2)를 구하기 위해 fibo(1)과 fibo(0)을 호출합니다
fibo(1)은 1의 결과값을 반환하고 종료됩니다(fibo를 호출하지 않습니다)
fibo(1)은 1의 결과값을 반환하고 종료됩니다(fibo를 호출하지 않습니다)
fibo(0)은 0의 결과값을 반환하고 종료됩니다(fibo를 호출하지 않습니다)

팩토리얼

팩토리얼 $N!$ 은 1부터 N까지의 모든 수를 곱한 값입니다.

def factorial(N):
    #N을 계속 줄이다가 1이 되면 종료합니다
    if N == 1:
        return 1
    return N * factorial(N-1) #factorial()함수 안에서 자신을 호출했습니다

4! = 4 x factorial(3)
factorial(3) = 3 x factorial(2)
factorial(2) = 2 x factorial(1)
factorial(1) = 1 (factorial을 호출하지 않습니다)

4! = 4 x factorial(3) = 4 x 3 x factorial(2) = 4 x 3 x 2 x factorial(1) = 4 x 3 x 2 x 1