[CryptoHack] Extended GCD

문제

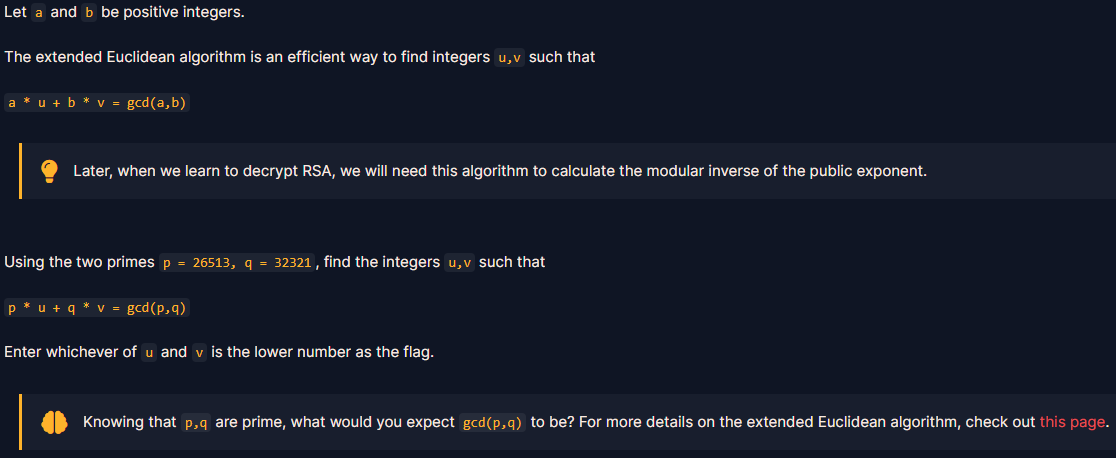
풀이

확장 유클리드 알고리즘을 사용하여 구한 u, v 중 작은 것이 flag이다.
우선 확장 유클리드 알고리즘을 이해하기 위해서는 베주 항등식에 대해 알고 있어야 한다.

베주 항등식(Bézout's Identity)

정수 a,b(적어도 둘 중 하나는 0이 아님)의 최대공약수를 d라고 할 때,
ax + by = d를 만족하는 정수 x,y가 반드시 존재한다.
+)정수 x,y에 대해 ax + by 꼴로 표현되는 모든 정수는 d의 배수이다.

확장 유클리드 알고리즘(Extended Euclidean Algorithm)

베주 항등식에 의해 $gcd(a,b) = d$라고 할 때, $ax + by = d$를 만족하는
정수 $x,y$가 존재하며 이는 유클리드 알고리즘의 과정을 역으로 계산하면 알 수 있다.

우선 유클리드 알고리즘의 과정을 식으로 표현하면 다음과 같다.

여기서 $r_{i+1}=r_{i-1}-r_iq_i$라는 식을 도출해낼 수 있다.

알고리즘의 종료 조건은 나머지가 0이 될 때이므로 $r_{i+1}=0$을 만족하는 시점이다.
그리고 d는 $r_i$이므로 $d=ax\;+\;by$ 꼴로 나타내기 위해 $r_0=a$, $r_1=b$라고 하면
$r_0=a\;*\;1\;+\;b\;*\;0$ 이고 $r_1=a\;*\;0\;+\;b\;*\;1$ 라고 할 수 있다.

이후 $r_i$들도 같은 꼴로 나타내어지기 때문에 $a$의 계수를 $s_i$, $b$의 계수를 $t_i$라고 할 때
$r_i\;=\;s_ia\;+\;t_ib$라는 식을 얻을 수 있다.

위 식을 $r_{i+1}=r_{i-1}-r_iq_i$의 $r$에 모두 대입해주면 다음과 같은 점화식을 얻을 수 있다.

계수 비교를 통해 최종적으로 다음 식들을 얻을 수 있다.

이제 이 식들을 구현해주자.

def EEA(a,b):
    r_0 = a; r_1 = b; s_0 = 1; t_0 = 0; s_1 = 0; t_1 = 1; q = 0; temp = 0

    while(r_1):
        q = r_0 // r_1
        temp = r_0
        r_0 = r_1
        r_1 = temp - r_0 * q
        temp = s_0
        s_0 = s_1
        s_1 = temp - s_0 * q
        temp = t_0
        t_0 = t_1
        t_1 = temp - t_0 * q
        print("%d = %d * %d + %d, %d, %d" %(r_0 * q + r_1, r_0, q, r_1, s_1, t_1))

EEA(32321,26513)

점화식 꼴이기 때문에 temp 변수를 사용하여 i를 1씩 늘려주며 계산하는 방식의 코드이다.

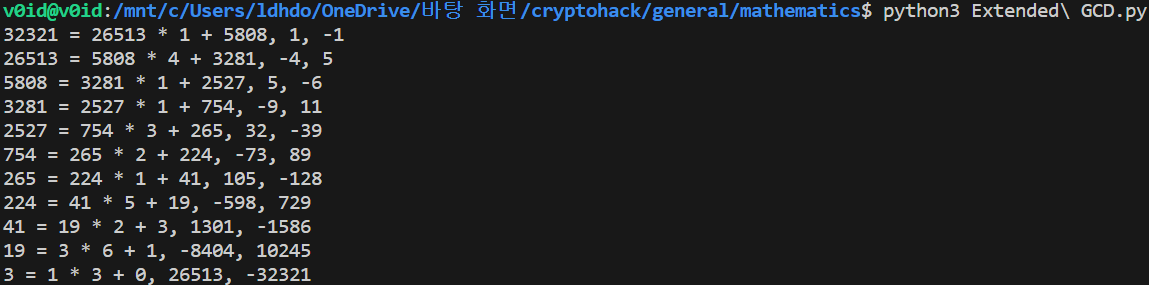
가장 마지막의 $s_i$와 $t_i$값이 $b$와 $-a$꼴로 나오는 것까지 확인할 수 있다.

FLAG = -8404